1. Attività didattiche
  2. Esame di Stato
  3. Forme indeterminate

Forme indeterminate

Introduzione

In questa attività viene viene assegnato un limite che, con il calcolo “a mano”, restituisce una forma indeterminata. Con l’uso della calcolatrice è possibile elaborare una congettura su quale possa essere il limite della funzione.

Gli strumenti utilizzati sono:

  • un esercizio svolto
  • 3 esercizi simili da proporre alla classe

Gli obiettivi di questa attività sono:

  • usare la calcolatrice per anticipare un risultato (elaborazione di una congettura)
  • imparare a utilizzare la calcolatrice come strumento di mediazione per affrontare l’argomento “forme indeterminate”

Esercizio svolto

Enunciato

Per il seguente limite

lim⁡x→0x3−xx2+x\lim_{x \to 0} \frac{{x}^3-x}{{x}^2+x}
  1. Esegui il calcolo “a mano” e verifica che si ottiene una forma indeterminata;
  2. Con l’aiuto della calcolatrice grafica NumWorks, elabora una congettura sul valore del limite;
  3. Riscrivi la funzione in modo equivalente, ma tale che il limite non sia più una forma indeterminata.

Svolgimento

  1. Calcoliamo “a mano”

    lim⁡x→0x3−xx2+x\lim_{x \to 0} \frac{{x}^3-x}{{x}^2+x} = 03−002+0\frac{{0}^3-0}{{0}^2+0} = 00\frac{0}{0}

  2. Sulla calcolatrice grafica NumWorks, nell’applicazione Funzioni, traccio il grafico della funzione f(x)=x3−xx2+xf(x)=\frac{{x}^3-x}{{x}^2+x} e osserviamo che in x=0 la funzione non è definita:

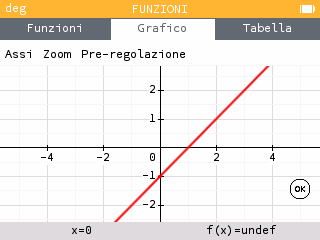
    limitex-0
    Tuttavia, per valori sufficientemente vicino a 0, f(x)f(x) è vicina a -1:
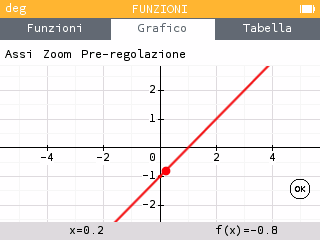
    limitex-02
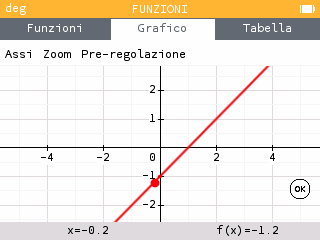
    limitex-meno02
    La nostra congettura è quindi che:
    lim⁡x→0x3−xx2+x=−1\lim_{x \to 0} \frac{{x}^3-x}{{x}^2+x}=-1

  3. Riscriviamo la funzione in modo equivalente, ma tale che il limite non sia più una forma indeterminata:

    lim⁡x→0x3−xx2+x=lim⁡x→0x(x2−1x+1=lim⁡x→0x(x+1)(x−1)x(x+1)=limx→0(x−1)=0−1=−1\lim_{x \to 0} \frac{{x}^3-x}{{x}^2+x}=\lim_{x \to 0} \frac{x({x}^2-1}{x+1}=\lim_{x \to 0} \frac{x(x+1)(x-1)}{x(x+1)}=lim_{x \to 0} (x-1)=0-1=-1
    Il risultato è −1-1.

Esercizi aggiuntivi

Per i seguenti limiti:

  1. Esegui il calcolo “a mano” e verifica che si ottiene una forma indeterminata;
  2. Con l’aiuto della calcolatrice grafica NumWorks, elabora una congettura sul valore del limite;
  3. Riscrivi la funzione in modo equivalente, ma tale che il limite non sia più una forma indeterminata.

    A) lim⁡x→0x3−6x2+5xx3−3x2\lim_{x \to 0} \frac{{x}^3-6{x}^2+5x}{{x}^3-3{x}^2}

    B) lim⁡x→1x2+2x−3x2+x−2\lim_{x \to 1} \frac{{x}^2+2x-3}{{x}^2+x-2}

    C) lim⁡x→2(1(x−2)2−1x2−2x)\lim_{x \to 2} (\frac{1}{{(x-2)}^2} - \frac{1}{{x}^2-2x})

    D) lim⁡x→1(1(x−1)−3x2−1)\lim_{x \to 1} (\frac{1}{(x-1)} - \frac{3}{{x}^2-1})

    E) lim⁡x→2(Xx−2−x2+14−x2)\lim_{x \to 2} (\frac{X}{x-2} - \frac{{x}^2+1}{4-{x}^2})

    F) lim⁡x→∞x−1x3−1\lim_{x \to ∞} \frac{x-1}{{x}^3-1}

    G) lim⁡x→∞x4−2x3\lim_{x \to ∞} \frac{{x}^4-2}{{x}^3}

    H) lim⁡x→∞1−x2x2−x\lim_{x \to ∞} \frac{1-{x}^2}{{x}^2-x}

    I) lim⁡x→∞x2−6x+9x2−3x\lim_{x \to ∞} \frac{{x}^2-6x+9}{{x}^2-3x}