Significato di un limite

Introduzione

In questa attività viene mostrato come inserire sulla calcolatrice NumWorks una funzione definita a tratti e come muoversi nella finestra per poter osservare i limiti sul grafico della funzione.

Gli strumenti utilizzati sono:

• un esercizio svolto
• 3 esercizi simili da proporre alla classe

Gli obiettivi di questa attività sono:

• prendere confidenza con la calcolatrice (quali sono i gesti meccanici che devo fare per definire una funzione e tracciarne il grafico)
• leggere i limiti su un grafico

Esercizio svolto

Enunciato

Sulla calcolatrice grafica traccia la funzione $f(x)$ e, osservandone il grafico, stabilisci i valori dei seguenti limiti: $f(x)= 2x$ se $x≤1$
$\quad$ $\quad$ $\qquad$ $\qquad$ $\qquad$ $\qquad -{x}^2$ se $x>1$

a. $\lim_{x \to -\infty} f(x)$
b. $\lim_{x \to +\infty} f(x)$
c. $\lim_{x \to 1^{-}} f(x)$
d. $\lim_{x \to 1^{+}} f(x)$
e. $\lim_{x \to 1} f(x)$

Svolgimento

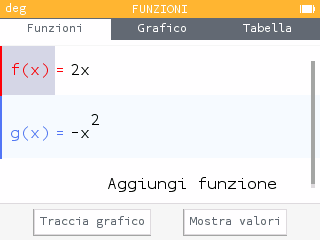
Nell’applicazione Funzioni, inseriamo le funzioni
$f(x)=2x$
$g(x)=-{x}^2$

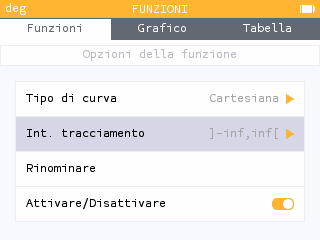
Per cambiare gli intervalli di definizione, selezioniamo la funzione $f(x)$ con le frecce direzionali (left up down right) e premiamo ok

selezioniamo Int. tracciamento

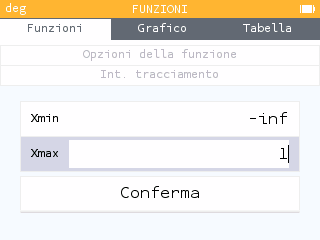
e modifichiamo Xmax con 1. Premiamo su Conferma.

Facciamo la stessa cosa con $g(x)$, ma questa volta modifichiamo Xmin con un valore molto vicino a 1, ma comunque maggiore di 1 (ad esempio: 1.001).
Premiamo il tasto back per tornare alla schermata di inserimento delle funzioni.
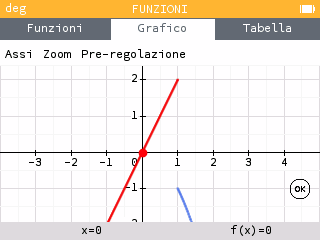
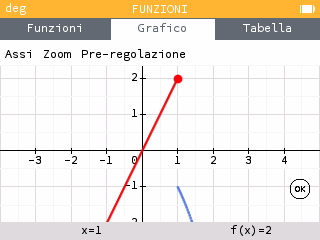
Da qui, tracciamo il grafico delle funzioni, utilizzando Traccia grafico in basso, oppure Grafico in alto, al centro.

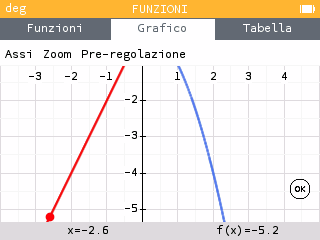
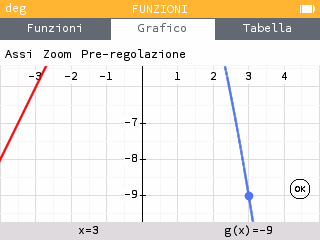
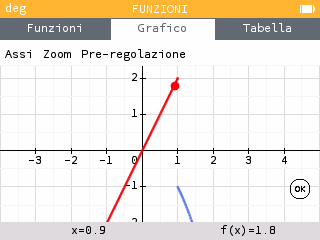
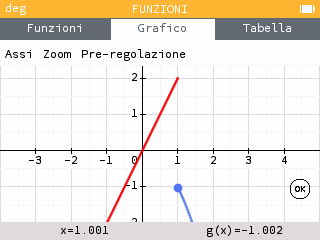
Possiamo muoverci con le frecce left / right per valutare i limiti:
$\lim_{x \to -\infty} f(x)=-∞$

$\lim_{x \to +\infty} f(x)=-∞$

$\lim_{x \to 1^{-}} f(x)=2$

$\lim_{x \to 1^{+}} f(x)=-1$

$\lim_{x \to 1^{-}} f(x) \neq lim_{x \to 1^{-}} f(x)$, quindi la funzione non ha limite per x che tende a 1.

Esercizi aggiuntivi

A) Sulla calcolatrice grafica traccia la funzione $f(x)$ e, osservandone il grafico, stabilisci i valori dei seguenti limiti:

$f(x)=x$ se $x≤2$
$\quad$ $\qquad {x}^2$ se $x>2$

a. $\lim_{x \to -\infty} f(x)$
b. $\lim_{x \to +\infty} f(x)$
c. $\lim_{x \to 2^{-}} f(x)$
d. $\lim_{x \to 2^{+}} f(x)$
e. $\lim_{x \to 2} f(x)$

B) Sulla calcolatrice grafica traccia la funzione $f(x)$ e, osservandone il grafico, stabilisci i valori dei seguenti limiti:

$f(x)={x}^2-9$ se $x$ $\ne$ $3$
$\quad$ $\qquad 0$ $\qquad$ altrimenti

a. $\lim_{x \to -\infty} f(x)$
b. $\lim_{x \to +\infty} f(x)$
c. $\lim_{x \to 3^{-}} f(x)$
d. $\lim_{x \to 3^{+}} f(x)$
e. $\lim_{x \to 3} f(x)$

C) Sulla calcolatrice grafica traccia la funzione $f(x)$ e, osservandone il grafico, stabilisci i valori dei seguenti limiti:

$$f(x)=\frac{x-|x|}{2x}$$

a. $\lim_{x \to -\infty} f(x)$
b. $\lim_{x \to +\infty} f(x)$
c. $\lim_{x \to 0^{-}} f(x)$
d. $\lim_{x \to 0^{+}} f(x)$
e. $\lim_{x \to O} f(x)$