Rapporto incrementale

Introduzione

In questa attività viene assegnata una funzione e si chiede di calcolare la derivata prima in un punto di ascissa data.
Con l’uso della calcolatrice NumWorks si può:

• calcolare il rapporto incrementale e assegnare via via dei valori sempre più piccoli al parametro h,
• tracciare la tangente al grafico nel punto di ascissa assegnato,
• tracciare il grafico della funzione derivata,
• calcolare il valore dell’ordinata nel punto di ascissa assegnato.

Gli strumenti utilizzati sono:

• un esercizio svolto
• alcuni esercizi simili da proporre alla classe

Gli obiettivi di questa attività sono:

• comprendere il significato di rapporto incrementale
• comprendere la corrispondenza che c’è tra la derivata prima di un punto e il coefficiente angolare della retta tangente in quel punto
• familiarizzare con il comando “diff(f(x),x,x)”

Esercizio svolto

Enunciato

Per ciascuna delle seguenti funzioni:

1. Calcola $f'(x0)$ “a mano” utilizzando il limite del rapporto incrementale, poi controlla il risultato sulla calcolatrice grafica
2. Calcola, nell’applicazione Calcolo, il rapporto incrementale per valori sempre più piccoli di h
3. Calcola, nell’applicazione Funzioni, la retta tangente nel punto di ascissa desiderato
4. Calcola, nell’applicazione Funzioni, il valore della funzione derivata nel punto di ascissa desiderato

Svolgimento

$$f(x)=3{x}^2-5x \qquad x_0=2$$

1. Calcoliamo “a mano” il rapporto incrementale

   $\frac{f(2+h)-f(2)}{h} = \frac{[3{(2+h)}^2-5(2+h)]-[(3\cdot{2}^2-5\cdot2)]}{h} =$
   $=\frac{[3(4+4h+{h}^2)-10-5h]-[3\cdot4-10]}{h}=$
   $=\frac{12+12h+{3h}^2-10-5h-12+10}{h}=\frac{{3h}^2+7h}{h}$
   Calcoliamo ora il limite per h tendente a 0 del rapporto incrementale:
   $\lim_{h \to 0} \frac{{3h}^2+7h}{h} = \lim_{h \to 0} \frac{h(3h+7)}{h} = \lim_{h \to 0} (3h+7) = 3\cdot0+7=7$
   Controllo il risultato sulla calcolatrice grafica NumWorks.

2. Calcoliamo nell’applicazione Calcolo il rapporto incrementale per un valori sempre più piccoli di h
   Nell’applicazione Funzioni dichiariamo la funzione $f(x)$
   

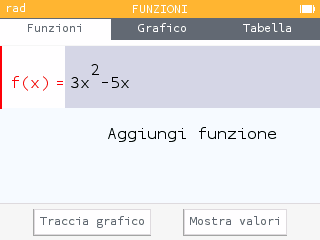
   Nell’applicazione Calcolo assegniamo al parametro h un valore molto basso, ad esempio 0,1, in virtù del fatto che dobbiamo stimare il valore del limite per h tendente a 0.
   (NB: Per farlo, digitare il valore che si vuole assegnare a h, ad esempio 0,01, e premere i tasti shift e pow. Una volta comparsa la freccetta, digitate h premendo prima il tasto alpha e, successivamente il tasto ok. Confermate premendo ok).
   Calcoliamo poi il valore del rapporto incrementale: $\frac{f(2+h)-f(2)}{h}$
   
   Assegniamo poi ad h un valore sempre più piccolo, ad esempio 0,01, poi 0,001, poi 0,0001 e osserviamo come, più h è “piccolo” e più il valore del rapporto incrementale si avvicina a 7.
   
   Suggerimento: Non è necessario digitare ogni volta il rapporto incrementale o il comando di assegnazione del parametro h. Ci si può muovere con up e poi premere ok per riprendere la riga desiderata, modificarla a piacere e poi premere ok per dare conferma.

3. Calcoliamo nell’applicazione Funzioni la retta tangente nel punto di ascissa desiderato

   Nell’applicazione Funzioni tracciamo il grafico della funzione e ci posizioniamo sul punto di ascissa x=2.
   
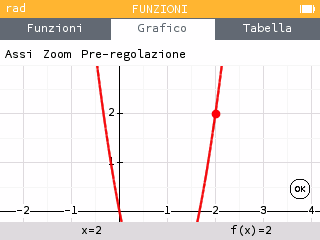
   Premiamo ok e selezioniamo Calcolare
   
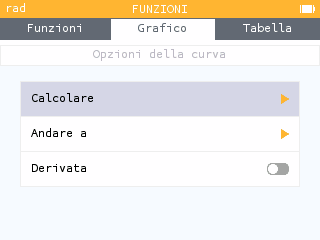
   e poi Tangente.
   
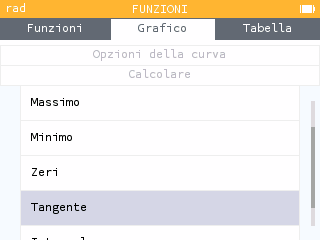
   Osserviamo che il coefficiente angolare della retta tangente è proprio 7
   
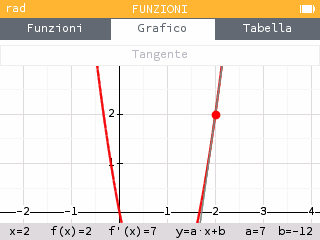
   (NB: L’esercizio A è con la stessa funzione di questo esercizio svolto, pertanto, per ottenere l’equazione e il grafico della retta tangente a $f(x)$ nel punto di ascissa $x_0=\frac{5}{6}$ è possibile muoversi con la freccia verso sinistra fino a raggiungere il punto desiderato, oppure digitare “5/6” sulla tastiera e premere ok).

4. Calcoliamo nell’applicazione Funzioni il valore della funzione derivata nel punto di ascissa desiderato

   Nell’applicazione Funzioni, nella scheda Funzioni aggiungiamo una funzione e premiamo il tasto toolbox,
   
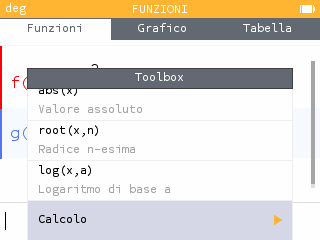
   selezioniamo Calcolo e poi selezioniamo il comando diff(f(x),x,a).
   
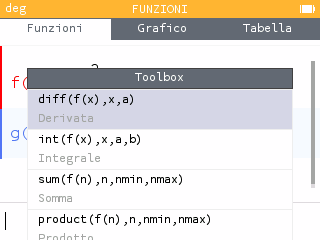
   Scriviamo diff(f(x),x,x) e tracciamo il grafico:
   
   
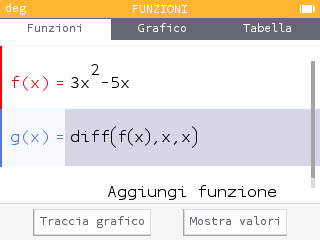
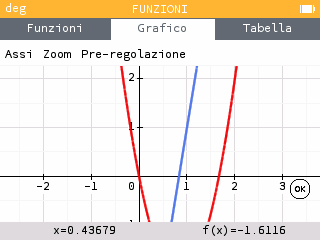
   Ci muoviamo con le frecce up e down per passare da una funzione all’altra.
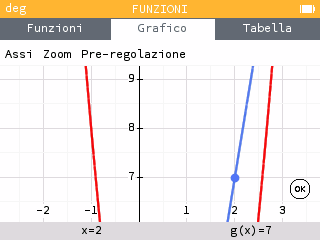
   Quando siamo sulla funzione g(x) possiamo muoverci con le frecce per andare al punto di ascissa 2, oppure > digitare 2 sulla tastiera e dare conferma con il tasto ok. Vediamo che g(2)=7, ovvero la derivata prima della funzione f(x) nel punto di ascissa x0=2 è proprio 7.
   
   (NB: Potremmo anche semplicemente inserire la funzione $f(x)$, tracciarne il grafico, premere il tasto ok, selezionare Derivata e confermmare con ok. Una volta giallo il simbolo a fianco alla dicitura Derivata, premere il tasto back e si potrà osservare che in basso, nella banda grigia, comparirà anche il valore della derivata prima nel punto. A questo punto, premendo il tasto 2il cursore ci porta nel punto di ascissa pari a 2, in cui la derivata prima è effettivamente pari a 7).

Esercizi aggiuntivi

Per ciascuna delle seguenti funzioni:

1. Calcola $f'(x0)$ “a mano” utilizzando il limite del rapporto incrementale, poi controlla il risultato sulla calcolatrice grafica
2. Calcola, nell’applicazione Calcolo, il rapporto incrementale per valori sempre più piccoli di h
3. Calcola, nell’applicazione Funzioni, la retta tangente nel punto di ascissa desiderato
4. Calcola, nell’applicazione Funzioni, il valore della funzione derivata nel punto di ascissa desiderato

A) $f(x)={3x}^2-5x \qquad x_0=\frac{5}{6}$

B) $g(x)={x}^2-3x+8 \qquad x_0=-2 \qquad x_1=3$

C) $h(x)=-{x}^3-5x \qquad x_0=0$

D) $p(x)=\frac{2}{x-2} \qquad x_0=4$

E) $f_0(x)=\sqrt{x-1} \qquad x_0=1 \qquad x_1=2$

ATTENZIONE è importante aver selezionato nelle Impostazioni Misura angolo : Radianti, altrimenti non si potranno stimare correttamente i limiti con funzioni goniometriche.

F) $f_1(x)=4\sin{x} \qquad x_0=\frac{\pi}{2}$

G) $f_2(x)=-2\cos{x} \qquad x_0=2\pi$

H) $f_3(x)=\sin{x}+\pi \qquad x_0=0$

I) $f_4(x)=\sin{x}-\cos{x} \qquad x_0=\frac{\pi}{4}$