Overall, this problem consists of selecting where to cut the wire, constructing a square from one piece and a circle from the other, and computing the area of each shape.
Let be the distance from the left end of the wire as shown below.

Cutting here will result in two pieces of wire, one with length and the other with length . Let the piece of wire with length be used to construct the circle and the piece of wire with length be used to construct the square.
For the circle, the length of the wire corresponds to the circumference of the circle. That is, . To determine the area of the circle, we must first solve for
Now we find the area of the circle using
For the square, the length of the wire corresponds to its perimeter. That is, . To calculate the area of the square, we must first determine the side length of the square. Since a square has 4 congruent sides, we have:
Now we find the area of the square using
The total combined area can be found by adding the two areas
Creating a Table
Using the area formula above, students may consider a guess-and-check method by trying out different values . A table of values for and its corresponding areas can be constructed.
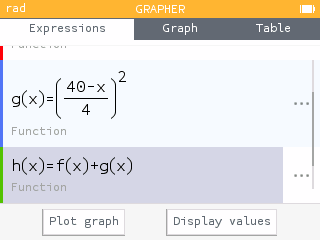
Using the Grapher app, input functions to compute the area of the circle, the area of the square, and the total area. Then view the Table tab and input possible values for .

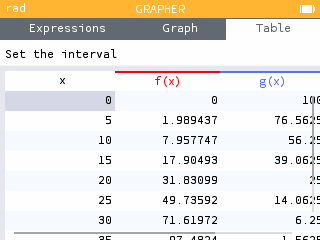
| x | Area of Circle | Area of Square | Total Area |
|---|---|---|---|
| 0 | 0 | 100 | 100 |
| 5 | 1.989 | 76.563 | 78.552 |
| 10 | 7.958 | 56.25 | 64.208 |
| 15 | 17.905 | 39.063 | 56.967 |
| 20 | 31.831 | 25 | 56.831 |
| 25 | 49.736 | 14.063 | 63.794 |
| 30 | 71.62 | 6.25 | 77.87 |
| 35 | 97.482 | 1.563 | 99.045 |
| 40 | 127.324 | 0 | 127.324 |
Using this approach, students will find the maximum at . That is, when the entire piece of wire is used to construct a circle, the area is maximized at .
Graphing
Using the area formula above, students may graph the function and look for maximums.
Using the Grapher app, enter the function .

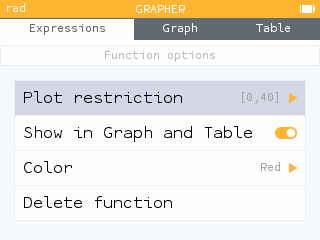
Before viewing the Graph, open the Function options by clicking on the three dots to the right of the expression. Adjust the plot restriction in the Function options to match the practical domain for this scenario.
Graphing the function, we see the maximum occurs at the right endpoint .
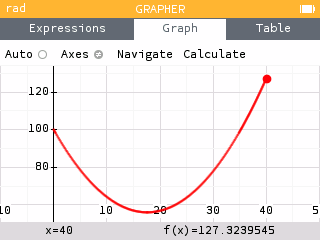
That is, when the entire piece of wire is used to construct a circle, the area is maximized at