Les mathématiques des anciens Égyptiens

Marianne Michel est titulaire d’un master de mathématiques et d’un doctorat en égyptologie. Elle donne aujourd’hui des conférences et des cours d’égyptien hiéroglyphique en parallèle de son travail d’informaticienne. Elle est l’auteur d’un ouvrage sur les mathématiques égyptiennes (Les mathématiques de l’Égypte ancienne. Numération, métrologie, arithmétique, géométrie et autres problèmes, Bruxelles, 2014) et partage avec nous des clés pour comprendre l’étendue des connaissances des anciens Égyptiens dans ce domaine.

Merci à elle d’avoir pris part à cet entretien et d’avoir partagé ses documents ainsi que ses propres illustrations !

Comment comptaient les anciens Égyptiens ?

Les anciens Égyptiens employaient le système décimal, tout comme nous, cependant il s’agit d’un système décimal non-positionnel, c’est-à-dire qu’ils employaient un symbole différent pour chaque base de 10, qu’ils répétaient, contrairement à nous qui employons seulement dix symboles en prenant en compte la position du chiffre pour distinguer les dizaines des centaines.

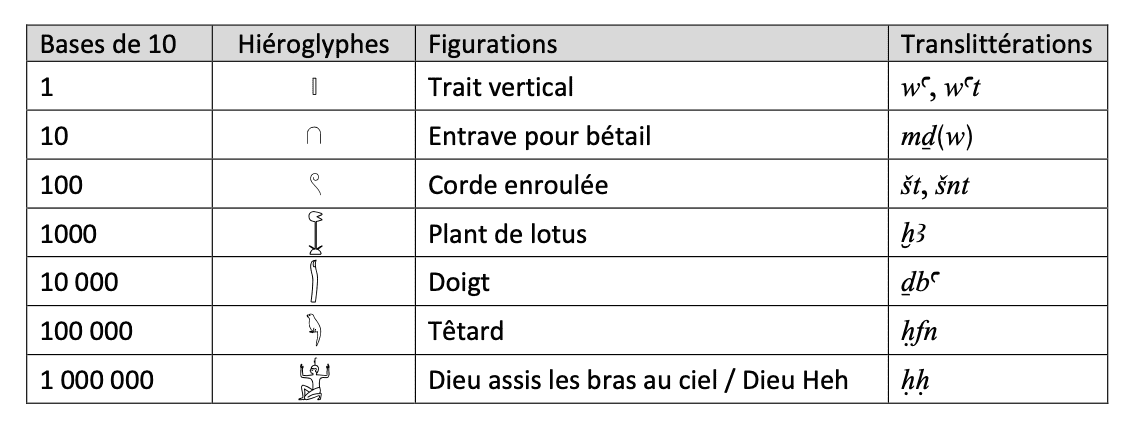
Les deux derniers signes du têtard et du dieu Heh peuvent également exprimer un “grand nombre” de manière indéterminée.

Ainsi, pour 7045 les Égyptiens écriront sept fois le symbole correspondant à mille, quatre fois dix et cinq fois un :

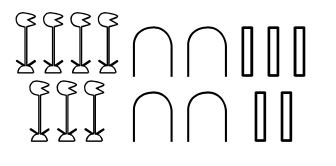
Ils n’utilisaient pas le zéro. On en a seulement quelques occurrences dans un décompte de marchandises où les quantités sont indiquées en lignes et en colonnes, comme on le ferait dans un tableur. C’est assez troublant ! On peut y lire le résultat d’un total qui est soustrait à un autre total. Il y est question de salaire en pain et en bière. Quand ces deux montants sont égaux, la différence est nulle : le résultat est alors marqué du symbole nfr qui veut dire “bon”, “bien”. Ce qui peut se comprendre comme : “Le compte est bon !”

Ils n’utilisaient pas non plus de chiffres négatifs. Les mathématiques de l’Égypte ancienne servaient principalement à distribuer du pain, calculer des surfaces de champs, des volumes de blocs de construction, … Les chiffres négatifs ne sont donc pas très utiles dans la vie quotidienne.

En revanche, ils utilisaient bien des nombres pouvant présenter une partie décimale. Pour exprimer ce qui se trouve en-dessous de l’unité, ils utilisaient des fractions, mais quasiment uniquement des fractions unitaires, c’est-à-dire dont le numérateur est égal à un. Ces fractions sont reconnaissables grâce au symbole de la bouche qui précède le nombre.

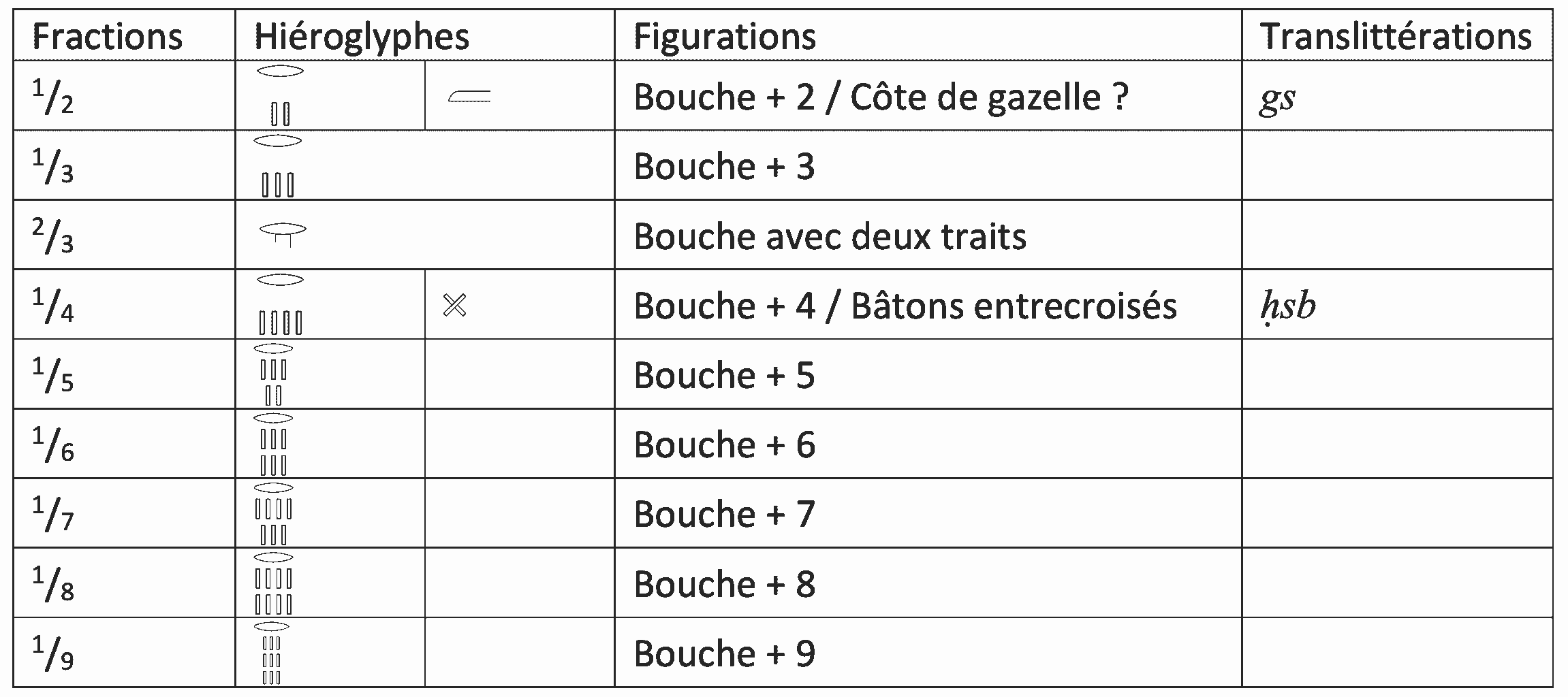
Et ces fractions ne peuvent pas être répétées : ¾ doit être écrit ½ (+) ¼. Toutes les fractions sont décomposées en fractions unitaire, écrites de la plus grande à la plus petite, les unes derrière les autres. On dispose d’une table qui donne la décomposition en somme de fractions unitaires de toutes les fractions doubles (c’est-à-dire de numérateur égal à 2) avec un dénominateur impair allant de 3 à 101. Et nous sommes bien dans l’impossibilité de trouver une méthode qui permettrait d’expliquer comment toutes ces décompositions ont été choisies !

Qu’est-ce qui caractérise les mathématiques égyptiennes ?

Les anciens Égyptiens maîtrisaient parfaitement le principe de proportionnalité, tant en arithmétique qu’en géométrie.

En arithmétique, pour résoudre des problèmes de recherches de quantités inconnues (l’équivalent des équations du premier degré ax = b), les anciens Égyptiens utilisaient entre autres la méthode de “fausse position”. Cette méthode consiste à “tester une valeur” (la fausse position) pour en déduire l’unique solution par proportionnalité.

Soit à résoudre l’équation ax = b, on pose une fausse position x’. à partir de cet x’, on évalue le résultat b’ donné par le calcul ax’ = b’. Ensuite, on tire parti du rapport entre le résultat voulu b et le résultat b’ pour déduire la valeur de l’unique et bonne solution x : (b/b’) multiplié par x’.

Les Égyptiens ne sont pas les seuls à avoir utilisé cette méthode, mais cela reste très malin !

En géométrie, pour assurer la régularité de construction d’une pyramide à base carrée, la manière la plus efficace est d’en contrôler l’angle des faces et ce, à chaque niveau d’élévation. C’est ici qu’intervient la mesure du seqed (sqd) qui exprime de combien la face latérale d’une pyramide “recule” pour une élévation donnée d’une coudée.

En pratique, une nouvelle assise de blocs d’une coudée de hauteur devait être “reculée” d’un seqed par rapport à la précédente, une nouvelle assise de blocs de deux coudées de hauteur devait être “reculée” de deux seqed par rapport à la précédente, etc.

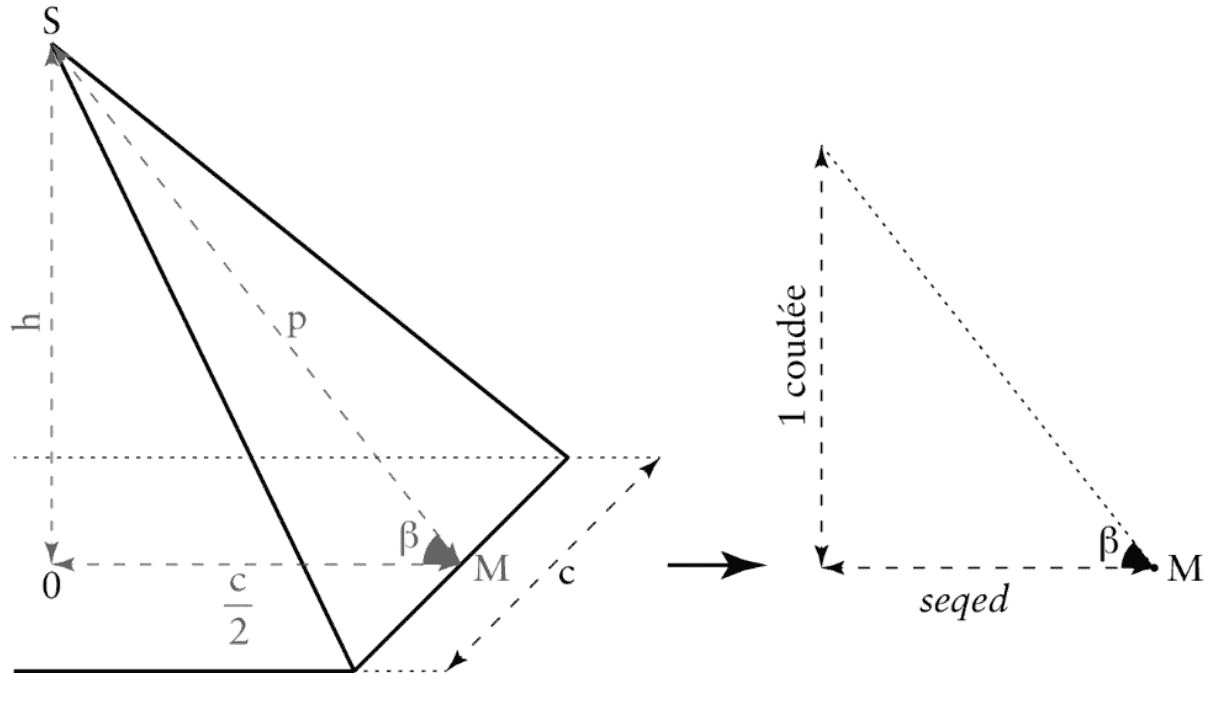
Quelles étaient leurs connaissances en arithmétique ?

Ils maîtrisaient bien sûr les opérations de base, qui sont décrites en toutes lettres dans les textes puisqu’il n’existe pas encore de symboles. La multiplication est traitée comme une addition. La division est traitée comme l’opération inverse de la multiplication.

Ainsi pour multiplier 12 par 12, l’ancien Égyptien écrivait :

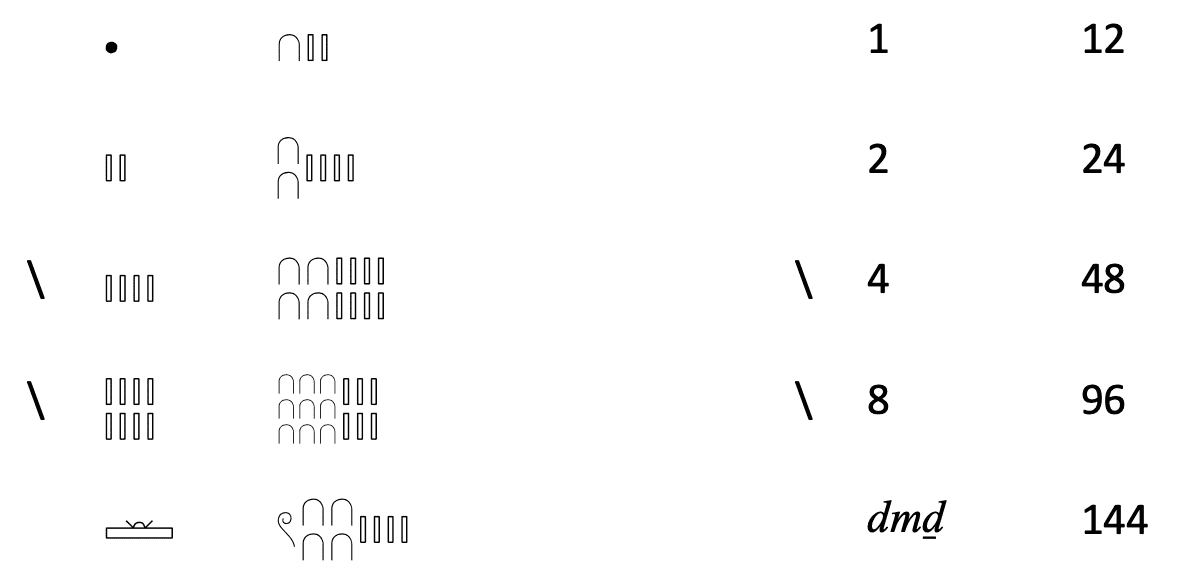
On rencontre dans les textes un certain nombre de problèmes pour lesquels le calcul de la racine carrée est nécessaire : pour calculer les dimensions d’un terrain, pour calculer le volume du tronc d’une pyramide, etc. “Prendre la racine carrée” est écrit qnb.t qui est représenté par un petit angle droit :

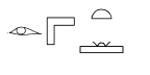
Au Moyen-Empire (NdA : environ -2100 à -1700), on connaît bien la racine carrée des carrés parfaits. On sait aussi que la racine carrée d’une fraction est égale à la fraction des racines carrées, ce qui n’est pas forcément évident !

Dans un papyrus démotique daté du 3e siècle avant J.-C., on trouve l’exemple du calcul de la racine carrée de 1500. Que fait le scribe ? D’abord, il simplifie son écriture, comme on le ferait aujourd’hui, en décomposant 1500 = 15 * 100. Il lui reste à déterminer la racine de 15. Le détail du calcul n’apparaît pas mais le scribe nous donne une solution approximative égale à 38+⅔+1/20. Soit une erreur relative de seulement 0,034% par rapport au résultat obtenu avec une calculatrice !

Dans un autre papyrus démotique un peu plus tardif, du début de la période romaine, on retrouve le calcul de la racine carrée de 10 avec la procédure de calcul, bien détaillée. Et quelle procédure : celle de Héron d’Alexandrie ! Rien de totalement surprenant jusqu’ici, puisque le texte est contemporain de Héron. Cependant, lorsque l’on applique cette méthode à la racine de 1500, on obtient exactement le résultat donné plus haut ! Donc au 3e siècle avant JC, la méthode d’extraction de la racine carrée était déjà connue des Égyptiens !

Et leurs connaissances en géométrie ?

Les anciens Égyptiens ont développé tout un vocabulaire pour parler de longueur, largeur, hauteur, … avec des termes parfois différents en fonction de la figure. Ils calculaient des surfaces de carrés, de rectangles, de disques etc… Ces calculs sont essentiels pour le cadastre, pour le relevé des récoltes.

On calculait également des volumes pour pouvoir résoudre des problèmes très pragmatiques. Par exemple, on a un grenier cylindrique dont on connaît la surface au sol : de combien doit-on l’élever pour qu’il puisse stocker une quantité donnée de grain ? D’ailleurs, dans leurs calculs, ils manipulent aussi les changements d’unités : les longueurs sont exprimées en coudées, les volumes de grain en coudées au cube mais aussi en unité de grain, qu’ils appellent le heqat.

En outre, on retrouve le calcul du volume d’une pyramide tronquée aussi, ce qui est remarquable ! Et dans des documents plus tardifs (du 3e siècle av. J.-C. au 1er siècle apr. J.-C.), on trouve même le calcul du volume d’une pyramide.

Et de toute l’Antiquité, bien avant Archimède, ce sont les anciens Égyptiens qui ont utilisé la meilleure approximation de pi : 3,1605.

Pour l’obtenir, ils ont approché l’aire d’un disque par l’aire d’un carré dont le côté vaut 8/9 du diamètre de ce disque. (Les Égyptiens ne décrivaient jamais un cercle par son rayon, mais uniquement par son diamètre.)

Imaginons que l’on souhaite calculer l’aire d’un disque de diamètre égal à 9 : le côté du carré associé vaut 8, et l’aire de ce carré est 64. Donc l’aire du disque vaut environ 64 (NdA : en réalité environ 63,62).

Quelles sont les sources dont nous disposons pour comprendre l’étendue des connaissances égyptiennes ?

Le corpus mathématique égyptien est extrêmement maigre. On pourra regretter que les problèmes offerts par les documents du Moyen Empire présente un niveau de difficulté moindre que celui du plus avancé des documents contemporains paléo-babyloniens. Mais la multitude de ces derniers (des centaines de fois plus nombreux) fait que la comparaison est d’emblée défavorable aux textes égyptiens.

La principale source dont on dispose en égyptologie pour les connaissances mathématiques est le papyrus Rhind, qui date du Moyen-Empire, et fait plus de 5 mètres de long. Sans lui, on ne saurait pas grand-chose sur les mathématiques égyptiennes ! C’est un véritable manuel de plus de 80 problèmes, bien classés, très didactique, avec des réponses détaillées. On y trouve des tables d’aide au calcul, des problèmes d’arithmétique, des calculs de surfaces, de volumes, d’inclinaisons et enfin des problèmes sur le pain et la bière. Ces problèmes relatifs au pain et à la bière, ce sont en réalité des problèmes de logistique : les ouvriers des chantiers étaient payés en pain et en bière, et ces produits dépendaient de la quantité de grain !

Tous les problèmes commencent par la même formule, que l’on traduit par “méthode pour…” calculer/procéder/vérifier. Il n’y a pas vraiment de généralisation, mais on nous décrit un protocole à suivre à partir de valeurs précises, d’exemples concrets.

Une autre grande source est le papyrus de Moscou.

L’écriture y est beaucoup plus grossière par rapport au papyrus Rhind et ses dimensions sont beaucoup plus réduites. Les problèmes n’y sont pas classés, les explications sont beaucoup plus courtes, moins développées. Malgré tout, ce modeste document se relève très intéressant ! Il contient par exemple le calcul du volume du tronc d’une pyramide … et selon la formule que l’on connaît aujourd’hui !

Ce qui est amusant c’est que les problèmes dans ce papyrus sont terminés par la formule gm.k nfr, que l’on peut traduire par “Tu as bien trouvé !” C’est en quelque sorte l’équivalent de notre “CQFD” !

Votre parcours est pour le moins atypique ! Pouvez-vous nous en parler rapidement ?

J’ai toujours été passionnée par l’histoire de l’Antiquité, et particulièrement par celle de l’Égypte, et ce depuis mes 10-12 ans.

Parallèlement à cela, au lycée (de 12 à 18 ans), j’étais dans la section latin-mathématiques. J’ai toujours adoré les mathématiques, c’est une matière qui m’a toujours fascinée : on commence par définir quelques objets, puis quelques lois sur ces objets, puis on construit des théorèmes, on met en évidence des résultats. C’est “propre”, rigoureux. En mathématiques, il n’y a pas de discussions, 1 + 1 sera toujours égal à 2 et jamais à 1,9 ou à 2,1. C’est net et cela me plaît.

A l’Université, j’ai voulu m’engager dans des études d’archéologie mais mon père a mis son veto : pas assez de débouchés ! J’ai donc choisi l’étude des mathématiques. J’ai enseigné en Belgique pendant un an, puis au Sénégal, mais je n’avais pas la sensation de pouvoir vraiment partager ma passion des mathématiques.

A mon retour du Sénégal, je me suis formée à l’informatique, ce qui m’a permis de travailler en divers endroits en France et en Belgique.

Et puis, en 2003, j’ai vécu mon premier voyage en Égypte et cela a été un véritable choc : toute ma passion pour l’Égypte ancienne s’est réveillée pour ne plus me lâcher. J’ai repris des études d’Orientalisme, en parallèle de mon travail d’informaticienne, à l’Université où je travaille. J’ai commencé par un master dit “complémentaire”, en travaillant les langues à écriture cunéiforme et l’égyptien hiéroglyphique, puis j’ai été admise à suivre un véritable master en orientalisme, option Égypte et Proche-Orient antiques. Sous l’impulsion d’un de mes professeurs pour qui il était évident que je devais utiliser mon bagage de mathématicienne, je me suis ensuite lancée dans un doctorat sur les mathématiques de l’Égypte ancienne. A l’heure actuelle, je continue mes activités de recherches et j’ai renoué avec l’enseignement en assurant de nombreux cours et conférences pour diverses associations égyptologiques.

Les mathématiques fonctionnent sur la base d’un ensemble d’axiomes et de postulats, tout comme une langue fonctionne suivant un ensemble de règles à suivre pour parler et écrire, une grammaire. Dans les deux cas, il s’agit de raisonner/d’interpréter en fonction de règles prédéfinies. On a l’habitude de séparer les enseignements dits “scientifiques”, des enseignements de type “littéraires” mais évitons de trop catégoriser ! Je pense que le grand intérêt que j’éprouve pour les textes mathématiques et les textes hiéroglyphiques s’explique par le fait que les uns et les autres sont, en quelque sorte, des textes “codés” !