Capture - Marquage - Recapture
Echantillonnage Programmation Python
Objectif
Approche de la notion de fluctuation d'échantillonnage puis mise en application de l'intervalle de confiance dans le cas d'un inventaire d'une espèce animale.
Savoir-faire
-
Quantifier l'effectif d'une population ou d'un taxon plus vaste à partir de résultats d'échantillonnage.
-
Estimer une abondance par la méthode de capture, marquage, recapture, fondée sur le calcul d'une quatrième proportionnelle.
-
Simuler des échantillons de même effectif pour visualiser la fluctuation d'échantillonnage.
-
En utilisant une formule donnée pour un intervalle de confiance au niveau de confiance de 95 %, estimer un paramètre inconnu dans une population de grande taille à partir des résultats observés sur un échantillon.
Partie 1 : Fluctuation d'échantillonnage
On s'intéresse à une très grande collection de billes. On décide d'en marquer 30% avec de la peinture avant de les mélanger avec les autres.
On souhaite maintenant effectuer des prélèvements de taille variable dans notre stock de billes et, dans chacun de ces échantillons, compter la part d'entre elles qui sont marquées avec de la peinture. Cette part sera t-elle proche des 30% effectivement marquées dans la population initiale ?
On peut réaliser cette expérience avec de vraies billes. On peut aussi réaliser l'expérience à l'échelle de la classe, avec des feuilles, des stylos, ou le matériel à disposition : essayez vous-mêmes ! Cependant, pour pouvoir réaliser nos expériences sur des échantillons en nombre et en taille variable (et surtout pour économiser du temps et des litres de peinture !), nous allons réaliser ici une simulation en Python.

Simulation d'un échantillon
On considère un échantillon de taille , c'est-à-dire composés de individus. Parmi eux, 30% sont marqués. La proportion d'individus marqués dans cette population est égale à 0,3.
Pour représenter cette expérience avec une simulation Python, on génère nombres aléatoires compris entre à l'aide de la commande random. Tous les nombres inférieurs à 0,3 symbolisent des individus marqués, les autres non. On compte ensuite dans l'échantillon le nombre d'individus marqués, c'est-à-dire le nombre de valeurs inférieures à 0,3.
-
Télécharger le script puis compléter la fonction
echantillon(t).from math import * from random import random from matplotlib.pyplot import scatter,show def echantillon(t): marque = ... for i in range(t): individu = random() if individu < ... : marque+=1 return ... -
Exécuter sur la calculatrice
echantillon(100)trois fois de suite. Quelles sont les valeurs obtenues ? Quelle interprétation peut-on en faire dans le contexte de notre énoncé ? -
Modifier le programme pour qu'il retourne non plus le nombre de valeurs inférieures à 0.3 mais leur fréquence par rapport à la taille de l'échantillon. Tester plusieurs fois la fonction avec
echantillon(50)puisechantillon(500). Qu'observe-t-on ?
from math import *
from random import random
from matplotlib.pyplot import scatter,show
def echantillon(t):
marque = 0
for i in range(t):
individu = random()
if individu < 0.30 :
marque+=1
return marque
Si le programme retourne par exemple 31, cela signifie que sur un échantillon de 100 billes, 31 d'entre elles étaient marquées avec de la peinture.
Il suffit de remplacer return marque par return marque/t sur la dernière ligne. Plus l'échantillon est grand, plus la fréquence obtenue est proche de 0,3.
Représentation graphique avec matplotlib
On souhaite maintenant procéder en même temps à l'étude de échantillons de taille . Pour cela, nous allons représenter graphiquement les différents résultats obtenus pour observer leur fluctuation avec la fonction graph(n,t) présente dans le même script.
-
Expliquer ce que fait le programme de la fonction
graph(n,t)sachant que la fonctionscatter(X,Y)du modulematplotlib.pyplotpermet de représenter un nuage de points utilisant la liste X en abscisses et la liste Y en ordonnées. On ne s'intéresse pas pour le moment aux lignes précédées du symbole # et qui ne sont pour le moment pas actives.def graph(n,t): x = [k for k in range(n)] y = [echantillon(t) for k in x] #compte = len([k for k in y if k>=0.3-1/sqrt(n) and k<=0.3+1/sqrt(n)]) #print(compte/n) scatter(x,y) show() -
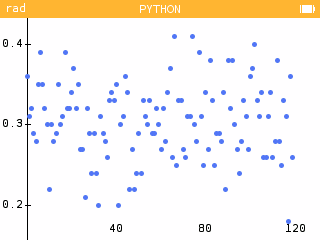
Lancer
graph(120,100)plusieurs fois. Autour de quelle valeur se répartissent les fréquences observées dans les échantillons ? Retrouve-t-on les résultats obtenus précédemment ? -
On supprime maintenant les symboles #, ce qui permet l'activation des deux lignes en fin de programme. Elles vont permettre de calculer la fréquence de résultats compris dans l'intervalle .
Lancer à nouveau
graph(120,100)plusieurs fois. Quelle valeur est retournée après l'affichage de la représentation graphique ? -
Quelle conclusion peut-on faire à partir de toutes nos observations ?
En est stockée une liste de entiers. En sont stockés les résultats successifs de la fonction echantillon(t) lancée fois (autant de fois qu'il y a de nombres dans la liste ). La fonction va donc permettre de représenter un nuage de points, chacun correspondant à une simulation de taille , répartis sur l'axe des abscisses, et dont l'ordonnée correspond à la fréquence obtenue pour chaque simulation.
Les valeurs se répartissent autour de 0.3, ce qui est effectivement la proportion théorique de billes marquées dans la population initiale. La large majorité des résultats se trouve entre 0,2 et 0,4.
On obtient généralement un résultat supérieur à 0.95.
Lorsque l'on prélève un échantillon dans une population pour y étudier la fréquence d'un caractère, la fréquence à laquelle on observe ce caractère varie : c'est la fluctuation d'échantillonnage. Lorsque la taille de l'échantillon augmente, les fluctuations diminuent et, dans au moins 95\% des cas, la fréquence observée est comprise entre et .
Partie 2 : Capture marquage recapture
On s'intéresse à une méthode de recensement de la population animale appelée couramment "capture marquage recapture" (CMR). Cette technique consiste à capturer une partie de la population étudiée et à en marquer tous les individus.
Par "marquage", on entend n'importe quelle technique permettant d'identifier un animal. On peut par exemple prendre en photographie ses marques naturelles. Il faut seulement s'assurer que ces marques sont uniques et ne peuvent pas être perdues, et s'il s'agit d'un marquage effectué par les chercheurs, elles ne doivent évidemment pas affecter la survie des individus. Les individus marqués sont ensuite relâchés dans leur environnement.
On procède par la suite à la capture d'un nouvel échantillon, dans lequel on recense les individus marqués. En faisant l'hypothèse que la fréquence d'individus marqués dans cet échantillon est proportionnelle au nombre d'individus marqués au sein de la population entière, on espère pouvoir établir un recensement relativement fiable de cette population.

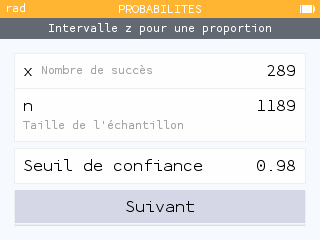
On procède ainsi à la capture et au marquage de 654 perruches dans une zone donnée. Lors de la recapture, on dénombre 289 individus marqués sur un échantillon de 1189 perruches.
-
En suivant le principe de la méthode CMR, à combien peut-on estimer la population totale de perruches dans cette zone ?
-
Pourquoi s'agit-il d'une estimation et non d'un chiffre exact ?
-
On appelle intervalle de confiance l'intervalle dans lequel se trouve une proportion avec une certitude de 95%. Cet intervalle se calcule avec la fréquence du caractère observée dans un échantillon de taille .
Dans notre exemple, quelle fréquence de perruches marquées observe-t-on lors de la recapture ? En déduire l'intervalle dans lequel se trouve la proportion (à 10-3 près).
-
En déduire un intervalle dans lequel se trouve la population totale de perruches.
-
L'intervalle obtenu par cette méthode doit cependant lui aussi être envisagé avec beaucoup de précautions. Selon vous, quelles sont les limites de la méthode CMR ?
On dénombre 289 individus marqués sur un échantillon de 1189 perruches. En faisant l'hypothèse que cette fréquence observée est proportionnelle au nombre d'individus marqués sur la population totale, on en déduit que avec N le nombre de perruches total présent dans la zone.
D'où une estimation de perruches au total dans cette zone.
Il est impossible de recenser tous les individus d'une population. La méthode CMR permet de faire un calcul sur la base d'un échantillon, or on a vu dans la première partie que lorsque l'on observe la fréquence d'un caractère dans un échantillon, les résultats sont fluctuants.
Le nombre de perruches dans le milieu a été calculée à partir d'une fréquence, fluctuante, il s'agit donc d'une estimation.
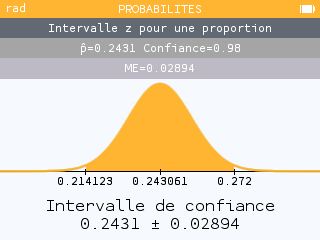
Lors de la recapture, la fréquence de perruches marquées est égale à 0,243 dans un échantillon de taille 1189. On obtient un intervalle de confiance égal à .
D'après notre intervalle de confiance, la proportion minimale d'individus marqués est égale à 0,214. Cette proportion représente le nombre d'individus marqués sur la taille totale de la poulation, soit . On en déduit qu'au maximum, la population compte individus.
A l'inverse, la proportion maximale d'individus marqués est à égale à 0,272 ce qui équivaut à une population de 2404 individus.
Donc, la population totale dans cette zone compte entre 2404 et 3056 perruches.
Il faut choisir soigneusement le temps écoulé entre les deux captures afin d'éviter de gros écarts dans la population (migration, fort taux de mortalité, ...) et à l'inverse, laisser le temps aux individus marqués de se mélanger à la population totale sans pour autant quitter la zone étudiée. Cette méthode fonctionne donc plutôt bien dans des milieux fermés. On peut aussi s'interroger sur les méthodes de marquage qui, lorsqu'elles ne sont pas naturelles, peuvent induire un stress sur les populations étudiées.
Astuce
Il est possible de calculer un intervalle de confiance avec la calculatrice. Attention toutefois, car la formule utilisée pour ce calcul n'est pas au programme du lycée et aboutit à un résultat beaucoup plus précis ! Cela permet toutefois de vérifier la cohérence des calculs.
Il suffit, dans l'application Probabilités, de sélectionner le menu Intervalles > Une proportion.
Dans notre exemple, le nombre de succès correspond au nombre de perruches marquées, soit 289, pour un échantillon de taille 1189. Par défaut, on peut laisser le seuil de confiance à 95% mais il est possible d'augmenter ce seuil de confiance pour obtenir un résultat moins précis. Ici, un seuil de confiance de 98% nous donne un résultat proche de celui que nous avons calculé.