Diagnostiquer une maladie par IA

Probabilités

Objectif

Construire un arbre de décision pertinent pour diagnostiquer une maladie puis réaliser un tableau de contingence pour évaluer l'efficacité de l'algorithme.

Savoir-faire

Corriger un algorithme ou un programme bogué simple.
À partir de données, par exemple issues d'un diagnostic médical fondé sur un test, produire un tableau de contingence afin de calculer des fréquences de faux positifs, faux négatifs, vrais positifs, vrais négatifs. En déduire le nombre de personnes malades suivant leur résultat au test.

On s'intéresse à un outil informatique permettant de diagnostiquer les différents problèmes d'entretien que peut rencontrer un propriétaire de plantes vertes.

Dans un premier temps, on s'intéresse à l'arbre de décision sur lequel est construit l'algorithme.

Arbre de décision

On propose un arbre de décision permettant de diagnostiquer le problème de soin que rencontre une plante verte.

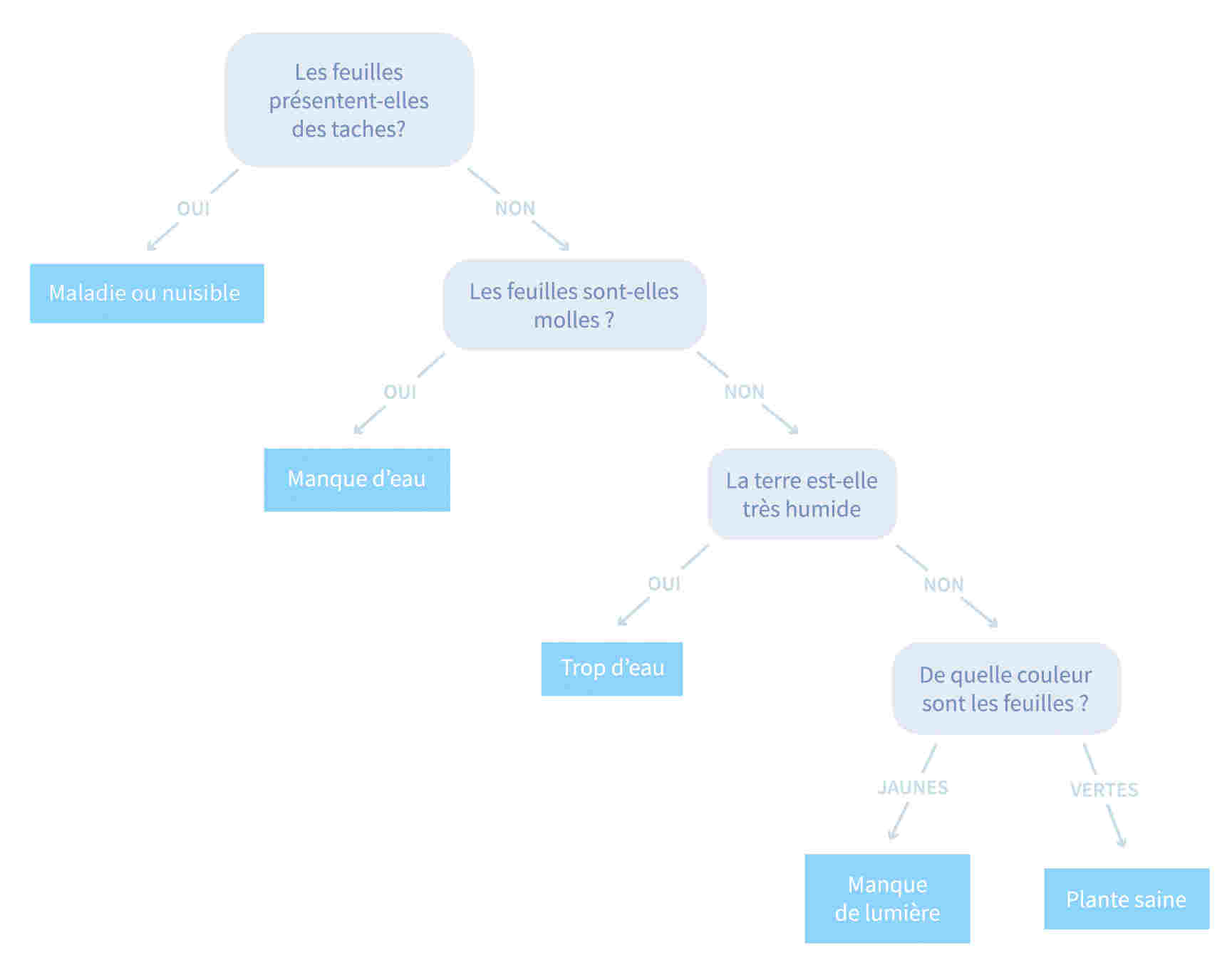
On considère un programme informatique suivant cet arbre de décision. A combien de questions faut-il répondre, au plus, pour diagnostiquer le problème ?

Au maximum, on peut identifier le problème en 4 questions.

Existe-t-il une situation où le problème sera diagnostiqué en une seule question ?

Si la plante est victime d'une maladie, il sera possible de poser un diagostic en une seule question.

Corriger les erreurs dans l'extrait de programme ci-dessous pour qu'il suive l'arbre de décision proposé.

if taches==True:
  return "Maladie ou nuisible"
else:
  if terreau_humide==True:
    return "Trop d'eau"
  else:
    if feuilles_molles==True:
      return "Manque d'eau"
    else:
      if couleur_feuilles=="vertes":
        return "Manque de lumière"
      elif couleur_feuilles=="jaunes":
        return "Plante saine"

if taches==True:
  return("Maladie ou nuisible")
else:
  if feuilles_molles==True:
    return("Manque d'eau")
  else:
    if terreau_humide==True:
      return("Trop d'eau")
    else:
      if couleur_feuilles=="jaunes":
        return("Manque de lumière")
      elif couleur_feuilles=="vertes":
        return("Plante saine")

On donne dans un tableau les caractéristiques relatives aux différents diagnostics réalisés par l'algorithme.

	Couleur des feuilles	Terre humide	Feuilles molles	Tâches sur les feuilles
Trop d'eau	jaune	oui	non	non
Manque d'eau	verte	non	oui	non
Manque de lumière	jaune	non	non	non
Maladie	verte	non	non	oui
Plante saine	verte	non	non	non

Proposer un arbre de décision différent qui permet de diagnostiquer le problème en trois questions, maximum.

Plusieurs arbres sont possibles, mais il suffit de commencer par la couleur des feuilles pour supprimer un noeud.

Tableau de contingence

On veut mettre à l'épreuve un autre programme permettant de détecter la présence de mildiou sur les plantes, une maladie causée par différents types d'organismes tels que les champignons.

On teste le programme sur 1 000 plantes. 60% des plantes souffrantes et 95% des plantes saines sont correctement diagnostiquées par le programme. Parmi les 1000 plantes étudiées, 800 sont effectivement malades.

On appelle sensibilité la probabilité qu'une plante malade soit diagnostiquée comme telle par l'algorithme. D'après l'énoncé, quelle est la sensibilité de notre test diagnostique ?

La sensibilité du test est égale à 0,6.

On appelle spécificité la probabilité qu'une plante saine ne soit pas diagnostiquée comme malade par l'algorithme. D'après l'énoncé, quelle est la spécificité de notre programme ?

La spécificité du test est égale à 0,95.

Quelle est la probabilité qu'une plante soit malade dans notre échantillon de test ?

La probabilité qu'une plante soit malade est égale à 0,8.

On appelle test positif un test concluant qu'une plante est malade. A l'inverse, un test négatif indique qu'une plante est saine (selon ce test).

Remplir le tableau de contingence ci-dessous à l'aide des données de l'énoncé.

	Test positif	Test négatif	Total
Malade
Saine
Total			1 000

	Test positif	Test négatif	Total
Malade	480	320	800
Saine	10	190	200
Total	490	510	1 000

On appelle valeur prédictive positive (VPP) la probabilité qu'une plante ayant été diagnostiquée comme malade soit effectivement malade.

On appelle valeur prédictive négative (VPN) la probabilité qu'une plante ayant été diagnostiquée comme saine soit effectivement saine.

Calculer les VPP et VPN. En conclure sur l'efficacité de notre algorithme.

Parmi les 490 plantes diagnostiquées comme malades, 480 le sont réellement d'où VPP = 0,98.

Parmi les 510 plantes diagnostiquées comme saines, 190 le sont réellement d'où VPN = 0,37.

Cela signifie qu'avec un test négatif, un plante a tout de même plus d'une chance sur deux d'être malade ! Le test n'est vraiment pas fiable lorsqu'il est négatif, on trouve beaucoup de "faux négatifs" dans nos résultats.

On appelle inférence bayésienne une méthode statistique destinée à calculer le degré de confiance à accorder à une hypothèse. Elle permet ici de répondre à la question suivante : "Sachant que le test est positif, quelle est la probabilité d'être effectivement malade ?"

On peut montrer facilement par le calcul que la réponse à cette question, même lorsque la sensibilité et la spécificité d'un test sont bonnes, dépend beaucoup de la proportion de la population touchée par la maladie !

L'inférence bayésienne est très utilisée dans la recherche. En effet, la question à laquelle nous venons de répondre dans le cadre de notre test diagnostique pourraît être posée très légèrement différemment : "Sachant que mes observations sont concluantes, quelle est la probabilité que mon hypothèse soit correcte ?" Question pertinente, non ?