Modèle de Hardy-Weinberg

On s'intéresse à une population de guppys, un petit poisson tropical, dans un grand bassin. On considère que la couleur du guppy dépend d'un gène particulier, pour lequel il n'existe que deux allèles appelés A et B.

On trouve dans le bassin des guppys jaunes, de génotype A//A, des guppys oranges de génotype A//B et des guppys rouges de génotype B//B.

Nous allons nous intéresser au processus de transmission à la génération suivante du gène responsable de la couleur.

Equilibre de Hardy Weinberg

On note $p$ la fréquence de l'allèle A et $q$ celle de l'allèle B. On rappelle qu'il s'agit des seuls allèles existant pour le gène étudié.

1. Quelle relation mathématique existe-t-il entre les fréquences alléliques $p$ et $q$?

Il s'agit des seuls allèles existant pour ce gène, d'où $p+q=1$.

2. Compléter ce tableau à double entrée qui répertorie les différentes combinaisons alléliques possibles en fonction des allèles transmis par la génération précédente.

   	A	B
   A	A//A	…
   B	…	…

3. On fait maintenant l'hypothèse d'une situation idéale dans laquelle notre population de guppys est très grande, isolée puisque dans un bassin particulier, à l'abri de toute prédation, et dans laquelle les reproductions se font au hasard sans mélange des générations. Cette population ne subit aucune mutation génétique, aucune dérive génétique.

   Le guppy jaune, de génotype A//A, est issu du croisement d'un gamète porteur de l'allèle A avec un autre gamète porteur de ce même allèle, de fréquence $p$. La probabilité d'obtenir un tel génotype à la génération suivante est donc $p^2$.

   Quelle est la probabilité d'obtenir à la génération suivante un guppy orange ? Et rouge ?

Le génotype B//B est obtenu avec une fréquence $q^2$ et le génotype A//B avec une fréquence $2pq$.

4. Quelle relation mathématique existe-t-il entre ces fréquences génotypiques ?

On a alors : $p^2+2pq+q^2 = 1$.

5. On cherche à montrer que les fréquence des allèles A et B, respectivement $f\left(A\right)$ et $f\left(B\right)$, dans la génération suivante sont respectivement égales à $p$ et $q$.

   1. Exprimer la fréquence allélique $f\left(A\right)$ en fonction des fréquences génotypiques $f\left(A//A\right)$ et $f\left(A//B\right)$.

   2. Substituer les fréquences génotypiques par leurs expressions telle que déterminées en question 3.

   3. Factoriser puis conclure.

   4. Même raisonnement pour déterminer $f\left(B\right)$.

Dans la génération suivante, on retrouve l'allèle A dans les génotypes A//A et A//B. On a donc : $\displaystyle f\left(A\right)=f\left(A//A\right)+\frac{1}{2}f\left(A//B\right)=p^2+\frac{2pq}{2}=p\left(p+q\right)=p$.

De la même manière, on peut montrer que $f\left(B\right)=q$.

Dans un cas idéal, les fréquences alléliques et génotypiques sont constantes d'une génération à l'autre. C'est l'équilibre de Hardy-Weinberg.

Par cas idéal, on entend que la population est de grande taille, n'a subi aucune mutation ni sélection naturelle, qu'il n'y a pas eu de migration et que les couples se font au hasard sans mélange des générations. Ces conditions sont rarement réunies dans la réalité mais le modèle de Hardy-Weinberg permet tout de même d'obtenir des éléments importants pour prédire l'évolution d'une population.

Application

On étudie une population de 700 guppys : 361 sont jaunes, 167 sont oranges et 172 sont rouges.

On souhaite savoir si cette population se trouve à l'équilibre de Hardy-Weinberg, c'est-à-dire si les fréquences alléliques et génotypiques sont constantes d'une génération à l'autre.

Tous les résultats seront arrondis à 0,001 près.

1. Déterminer la fréquence de chaque génotype dans cette population de guppy.

On a $\displaystyle f\left(A//A\right)=\frac{361}{700}=0,516$, $\displaystyle f\left(A//B\right)=\frac{167}{700}=0,239$ et $\displaystyle f\left(B//B\right)=\frac{172}{700}=0,246$.

2. On note $p$ la fréquence de l'allèle A et $q$ celle de l'allèle B. On rappelle qu'il s'agit des seuls allèles existant pour le gène étudié.

   Calculer, à partir des résultats précédents, les fréquences alléliques $p$ et $q$.

$\displaystyle p=\frac{361}{700} + \frac{1}{2}\times\frac{167}{700}=0,635$

$\displaystyle q=\frac{172}{700}+\frac{1}{2}\times\frac{167}{700}=0,365$

3. On fait maintenant l'hypothèse que notre population se trouve à l'équilibre de Hardy-Weinberg. Dans ce cas, calculer les fréquences génotypiques attendues pour la génération suivante.

Si notre population est à l'équilibre de Hardy-Weinberg, alors on aura pour la génération suivante :

$f\left(A//A\right)=p^2=0,635^2=0,403.$

$f\left(A//B\right)=2pq=2\times 0,635\times 0,365=0,464$

$f\left(B//B\right)=q^2=0,365^2=0,133$

4. Comparer les fréquences attendues à la génération suivante à celles de la génération actuelle. Ces fréquences sont-elles stables ? La population se trouve-t-elle à l'équilibre de Hardy-Weinberg ? Commenter le résultat.

Les fréquences attendues à la génération suivante sont très différentes des fréquences génotypiques observées dans la population. Par exemple, d'après notre raisonnement, c'est le génotype A//B qui sera le plus répandu à la prochaine génération et non plus le génotype A//A. La population ne se trouve donc pas à l'équilibre de Hardy-Weinberg.

Dans le cas étudié ci-dessus, la différence de résultat est très marquée et la conclusion ne pose pas de problème. Cependant il existe un test statistique qui permet de conclure si les différences observées entre les fréquences observées et les fréquences calculées sont significatives : le test du khi-deux d'adéquation.

Sur la calculatrice NumWorks, il suffit de se rendre dans l'application Statistiques > Tests statistiques > Khi-deux > Adéquation et de remplir les données dans le premier tableau. L'écran suivant fournit des données pré-calculées que l'on peut valider, et le dernier écran établit une conclusion : l'hypothèse d'adéquation entre les résultats observés et les résultats calculés est rejetée.







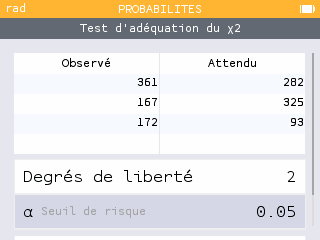
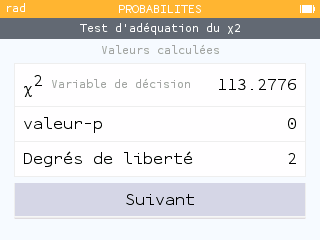
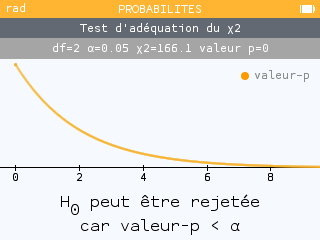
Si la population ne se trouve pas à l'équilibre de Hardy-Weinberg pour ce gène, cela signifie que l'une des conditions du modèle n'est pas respectée. Si la population se trouve dans un bassin, on peut éliminer l'hypothèse d'une migration. On peut en revanche poser l'hypothèse que la reproduction ne se fait pas complètement au hasard : la couleur du mâle ou de la femelle peut jouer un rôle dans le choix du partenaire.

En Python

On peut réaliser un programme Python relativement simple pour calculer automatiquement les fréquences génotypiques dans une population ainsi que celles de la génération suivante en supposant que celle-ci est à l'équilibre de Hardy-Weinberg. Au début du programme, l'utilisateur est invité à entrer les effectifs E1, E2 et E3 correspondant respectivement aux individus de génotype A//A, A//B et B//B. Pour cela, on utilisera la commande E1=int(input("E1=")) qui permet d'afficher "E1=" à l'écran et d'affecter l'entier entré par l'utilisateur à la variable E1.

On utilisera aussi la commande round(valeur,n) qui permet d'arrondir une valeur à n décimales.

On propose de télécharger puis compléter le programme suivant :

E1=int(input("E1="))
E2=int(input("E2="))
E3=int(input("E3="))
pop= .....
print("On a :")
print("f1=",round( ... /pop,3))
print("f2=",round( ... /pop,3))
print("f3=",round( ... /pop,3))
p=(E1+0.5*E2)/pop
q=(E3+0.5*E2)/pop
print("Et à la génération suivante :")
print("f1=",round( ... ,3))
print("f2=",round( ... ,3))
print("f3=",round( ... ,3))
    

Astuce : pour compléter le script sur la calculatrice, il est conseillé d'utiliser la touche var qui permet de retrouver plus rapidement toutes les variables déclarées dans le script. Il suffit de sélectionner la variable souhaitée et de valider avec la touche OK pour qu'elle s'inscrive à l'écran !

E1=int(input("E1="))
E2=int(input("E2="))
E3=int(input("E3="))
pop=E1+E2+E3
print("On a :")
print("f1=",round(E1/pop,3))
print("f2=",round(E2/pop,3))
print("f3=",round(E3/pop,3))
p=(E1+0.5*E2)/pop
q=(E3+0.5*E2)/pop
print("Et à la génération suivante :")
print("f1=",round(p**2,3))
print("f2=",round(2*p*q,3))
print("f3=",round(q**2,3))