Evaluation de la population de loups en France

Cette activité est proposée par Guillaume Lorimier, professeur de mathématiques au lycée Madame de Staël à Saint-Julien-en-Genevois.

On s'intéresse à des documents relatifs à l'évaluation de la population de loups en France. Ces effectifs font l'objet de deux approches :

• l'EMR (effectif minimum retenu), établi sur la base d'indices relevés sur le terrain (traces au sol, observation directe, …) ;

• la CMR (capture-marquage-recapture), reposant sur l'analyse génétique d'échantillons, et a-priori corrélée à l'EMR par une fonction mathématique. La méthode CMR permet aussi, par le calcul, de prendre en compte le risque de non-détection d'un individu sur le terrain.

Document 1 : Estimation des effectifs

L'estimation des effectifs de la population de loups s'appuie sur des méthodes dites de « Capture-Marquage-Recapture » (CMR) qui tiennent compte de la détection imparfaite des animaux. En pratique, il s'agit de détections des profils génétiques établis sur les indices biologiques dont le traitement engendre un délai incompatible avec une mise à jour annuelle en temps réel. Les bilans annuels de population font ainsi appel à une projection de l'indicateur de tendance démographique, l'EMR (« Effectif Minimal Retenu »), résultat de la somme des tailles de groupe minimum de loups détectés durant l'hiver par le Réseau Loup-Lynx, corrigé par une fonction mathématique le reliant à la CMR.

Source : Note technique de l'Office Français de la Biodiversité (OFB) et du CNRS, novembre 2020.

Document 2 : Relation mathématique entre CMR et EMR

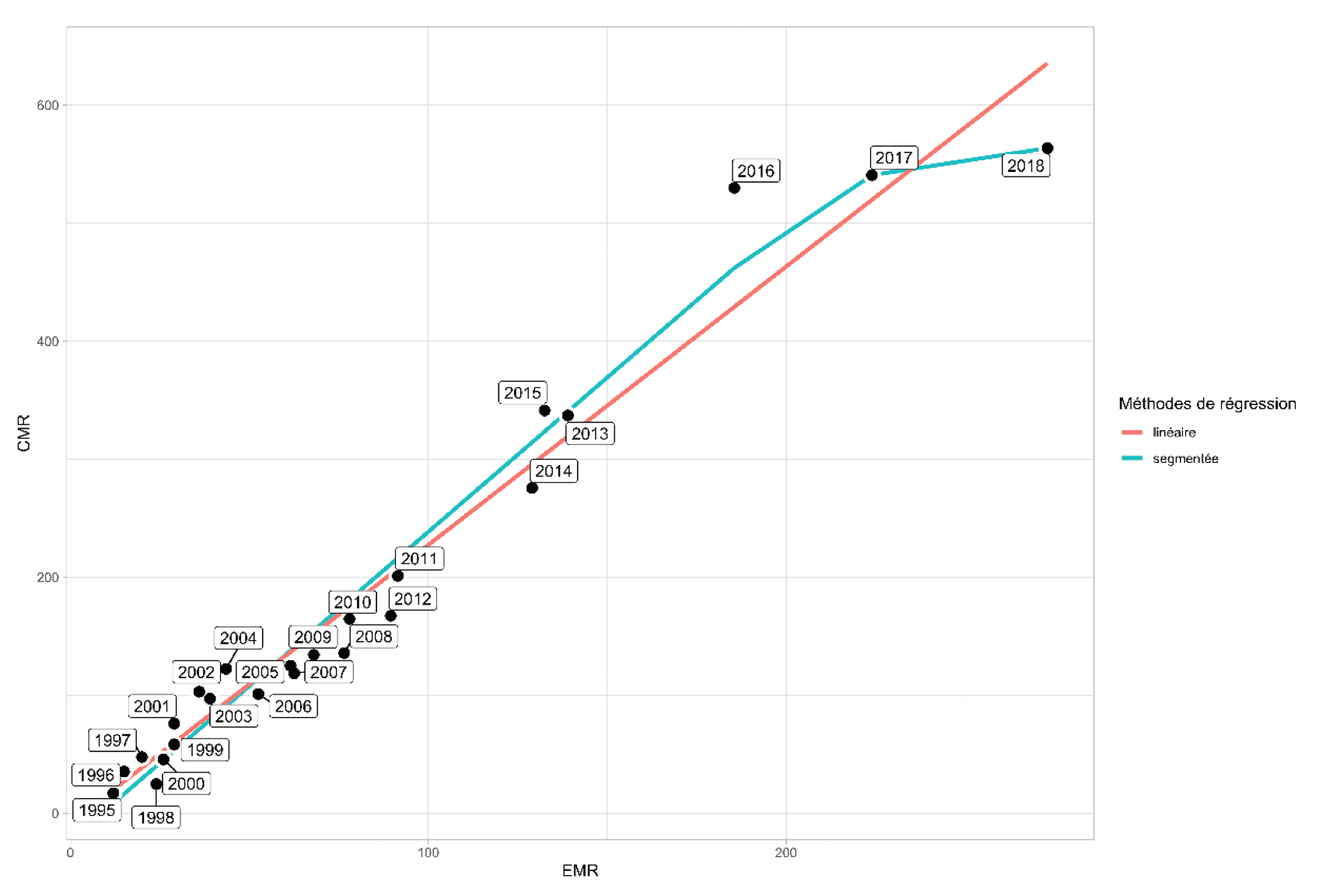
Ajustement par régression linéaire simple (courbe rouge) et avec une régression segmentée dite "par morceaux" (courbe bleue). La régression segmentée est statistiquement la meilleure pour décrire la relation entre données CMR et données EMR.

Note technique de l'Office Français de la Biodiversité (OFB) et du CNRS, novembre 2020.

1. Pourquoi les bilans annuels de la population ne sont-ils que des projections et ne sont pas le résultat direct des conclusions de la méthode CMR ?

La méthode CMR repose sur des analyses génétiques qui nécessitent du temps, ce qui "engendre un délai incompatible avec une mise à jour annuelle en temps réel". Ainsi, les données récentes établies par CMR sont en réalité des projections basées sur un autre paramètre, l'EMR, qui repose sur l'exploitation d'indices directs.

2. On constate une corrélation mathématique entre EMR et CMR, ce qui permet de réaliser des projections des effectifs CMR de l'année en cours. Justifier l'utilisation d'un modèle de régression linéaire pour exprimer la relation entre EMR et CMR pour les données antérieures à 2015.

Lorsque les données anciennes des EMR sont mises en relation avec les résultats de CMR dans un graphique, celles-ci semblent alignées selon une droite qui passe par l'origine. Il semblerait donc qu'il existe une relation de proportionnalité entre ces données, d'où l'utilisation d'une droite de régression linéaire pour estimer les résultats de CMR à partir de l'EMR.

3. Évaluer le coefficient de proportionnalité de la droite de régression linéaire.

On trouve un coefficient de proportionnalité aux alentours de 2,3.

4. On évalue un EMR pour l'année 2019 égal à 301. Proposer une estimation de l'effectif selon la méthode CMR en 2019 en suivant le modèle de régression linéaire.

En utilisant un coefficient de proportionnalité égal à 2,3, on obtient une estimation de 692 pour les données CMR.

5. Pourquoi les résultats à partir de l'année 2016 laissent-ils à penser qu'il est nécessaire de procéder à un changement de modèle ?

Si les données anciennes semblent alignées selon une droite correspondant à un modèle de régression linéaire (en rouge), les trois dernières valeurs (et plus particulièrement celles de 2016 et 2018) ne sont plus alignées sur cette droite. Il semblerait que le modèle ne soit donc plus tout à fait valable, d'où l'utilisation dans le document 2 d'un autre type de régression, dite segmentée, qui semble statistiquement plus fiable pour décrire la relation entre les données.

Document 3 : Recueil des données CMR

L'estimation des effectifs de la population de loups en France s'appuie sur un modèle d'estimation des paramètres démographiques dit de Capture-Marquage-Recapture ou CMR (Cubaynes et al, 2010). Le travail du Réseau Loup/Lynx sur le terrain permet d'échantillonner les animaux présents in situ à l'échelle de toute la France au travers des relevés d'indices de présence laissés par les animaux. La technique CMR pour le suivi du loup profite donc de ce suivi à grande échelle pour adopter une démarche non invasive de capture et marquage au travers des profils génétiques individuels des animaux présents au travers des excréments, poils, urines, sang ou tissus qu'ils ont laissés sur le terrain. Ce suivi biomoléculaire individuel permet alors de tenir compte de la détection imparfaite des individus que l'on suit dans la nature (voir Lebreton et al, 1992 pour la méthode).

Note technique de l'Office Français de la Biodiversité (OFB) et du CNRS, novembre 2020.

Document 4 : Estimation des effectifs

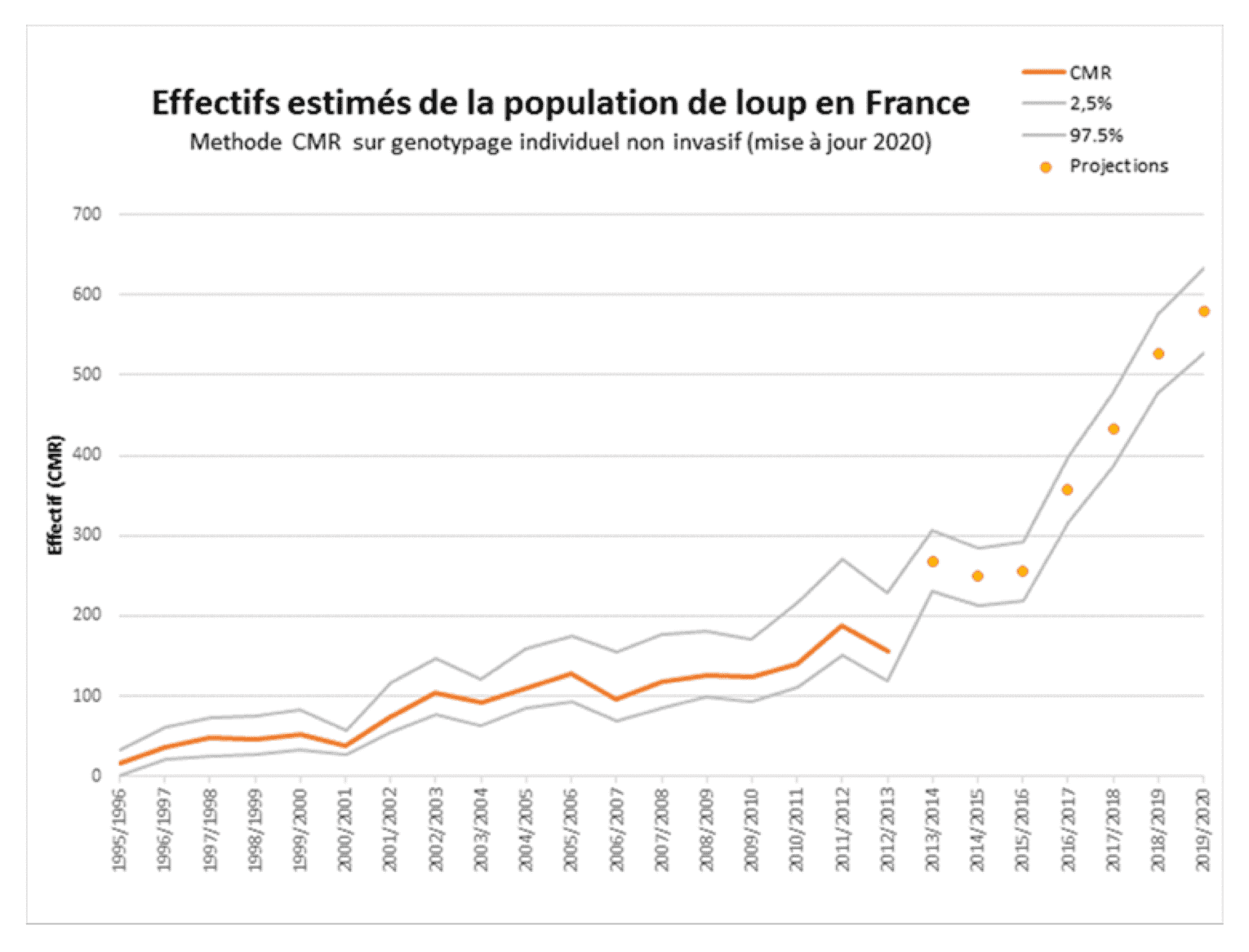
Effectifs estimés de la population de loups en France en sortie d'hiver 2019-2020. Le trait orange mesure la taille de la population par CMR, Les points de 2013-2014 à 2019-2020 (ronds oranges) sont déduits par projection sur la base de la relation CMR=f(EMR) calibrée en 2014, sous l'hypothèse d'un fonctionnement similaire de la population. L'effectif estimé en sortie d'hiver 2019-20 était de 577 individus.

Note technique de l'Office Français de la Biodiversité (OFB) et du CNRS, novembre 2020.

6. Pourquoi la méthode CMR de génotypage individuel est-elle décrite comme non-invasive ?

Le marquage employé dans cette étude repose en réalité sur un suivi génétique des individus à partir de résidus laissés sur leur passage. Les excréments et traces diverses laissées par les loups sont analysés, afin de permettre l'identification des individus. Ainsi, le marquage n'est pas invasif car il ne nécessite pas d'intervention sur l'animal.

7. L'estimation de la population à la sortie de l'hiver 2019-2020 était de 577 individus. Ce chiffre est en hausse de 9% par rapport à l'année précédente. Quelle était donc l'estimation à la sortie de l'hiver 2018-2019 ? On arrondira bien sûr le résultat à l'entier.

Le chiffre représente une hausse de 9% par rapport à l'année précédente, l'effectif a donc été multiplié par 1,09. La population à la sortie de l'hiver 2019-2020 était donc estimée à 529 individus.

8. Si l'évolution reste la même pendant l'année suivante, quel effectif peut-on prévoir pour la sortie de l'hiver 2020-2021 ?

Si la population augmente à nouveau de 9%, l'effectif sera de 629 individus à la sortie de l'hiver suivant.

9. Un document plus récent estime le nombre de loups à la sortie de l'hiver 2020-2021 à 624 individus. Que penser de notre prévision ? Quel a été le taux d'évolution par rapport à l'année précédente ?

Nos estimations étaient au-dessus de la réalité, mais de peu. Le taux d'évolution a en réalité été de 8%.

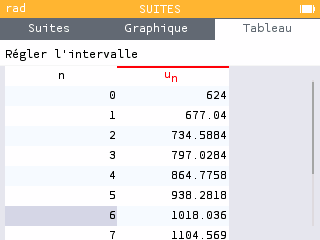
10. On fait l'hypothèse que le taux d'évolution reste de 8.5% à partir de l'hiver 2020-2021. On note $n$ le nombre d'hivers écoulés à partir de cette date et on note $u\left(n\right)$ l'effectif estimé. Par exemple, $u\left(1\right)$ correspond à l'estimation de l'effectif à la sortie de l'hiver 2021-2022.

    A l'aide d'une suite géométrique et de votre calculatrice, estimer combien d'années seront nécessaires pour que la population dépasse les 1000 individus.