Le jeu de croix ou pile

Présentation du jeu

Dans un article de son Enyclopédie, d'Alembert étudie le jeu de croix ou pile. Ce jeu consiste à lancer deux fois de suite une pièce sur laquelle figure une croix sur l'une de ses faces, et un pilier sur l'autre. Le jeu est gagné dès lors que l'on obtient une croix.

Il s'agit en réalité d'un jeu de pile ou face, mais les rois n'ont pas toujours figuré sur leurs propres pièces. A la place était représentée une croix et l'expression a perduré : "face" était donc "croix" !

Si lors du premier lancer, le joueur obtient "croix", le jeu s'arrête car le joueur a gagné. En revanche, s'il a obtenu "pile", il doit relancer la pièce. S'il obtient "croix", c'est gagné. Sinon, c'est bien sûr perdu.

Dans son article, d'Alembert s'intéresse à la mise qu'il convient de placer afin que le jeu soit équitable.

1. Représenter la situation à l'aide d'un arbre de probabilités.



2. Deux points de vue s'opposent. D'Alembert estime qu'il y a trois issues possibles car gagner au premier lancer met fin au jeu : "croix" au premier lancer, "croix" au second, et ne pas obtenir croix. Il y a donc 2 chances sur 3 de gagner. Pour d'autres mathématiciens, comme Bernoulli, cette probabilité est de 3/4. Que pensez-vous de ces deux affirmations ?

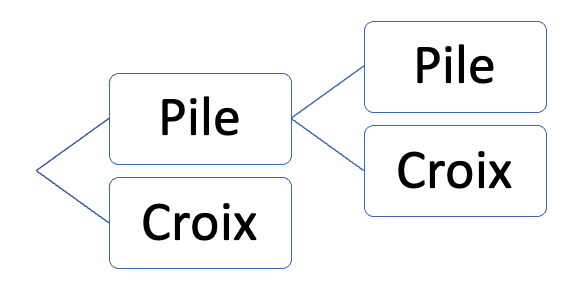
Modélisation avec Python

On propose de réaliser un court programme permettant de simuler un très grand nombre de lancers de pièces afin de déterminer par l'expérience laquelle de ces deux affirmations semble la plus correcte.

1. Ecrire une fonction piece() qui renvoie True si la pièce tombe sur "croix", et False si elle tombe sur "pile".

   Pour cela, on utilisera la fonction random() qui permet d'obtenir un nombre aléatoire compris dans l'intervalle [0;1[ : si le nombre est inférieur à 0,5 on considère avoir obtenu "croix", sinon "pile". Cette fonction se trouve dans le module random qu'il faut donc importer au début du script à l'aide de la commande from random import *.

   Tester le programme plusieurs fois pour vérifier l'algorithme.

from math import *
from random import *
def piece():
  if random()<0.5:
      return True
  else:
      return False
    

2. Ecrire dans le même script une fonction jeu() qui modélise le jeu de croix ou pile, c'est-à-dire que la fonction doit renvoyer True si la pièce tombe sur "croix" au premier ou au second lancer, False sinon.

   Tester le programme 10 fois. Combien de réussites avez-vous obtenues ?

def jeu():
  if piece()==True:
    return True
  else:
    if piece()==True:
      return True
    else:
      return False
    

3. Le résultat obtenu lors de la série précédente est-il représentatif ?

On a vu en classe de Seconde qu'un échantillon n'était pas toujours représentatif, particulièrement lorsque cet échantillon est restreint.

4. On propose de simuler l'expérience un très grand nombre de fois et de comptabiliser le nombre de réussites dans une variable X.

   Compléter la fonction simul(n) qui simule $n$ jeux et retourne la fréquence de réussites :

   def simul(n):
     X= ...
     for i in range( ... ):
       if jeu()== ... :
         X+=1
     return ...
   

def simul(n):
  X=0
  for i in range(n):
    if jeu()==True:
      X+=1
  return X/n
    

5. Lancer des simulations pour 100, 500 puis 1000 lancers. Lequel de nos mathématiciens semble avoir raison d'après notre expérience ? Comment l'expliquer ?

Plus on multiplie les tirages et plus le résultat tend vers 0,75. C'est donc Bernoulli qui avait raison et le raisonnement erroné de d'Alembert lui valut d'ailleurs quelques moqueries de la part de ses confrères.

On pourra proposer aux élèves de raisonner à l'inverse pour se convaincre de la réalité de ce résultat : quelle est la probabilité de perdre ? On en déduit ainsi la probabilité de gagner.

Un jeu équilibré

On imagine qu'en jouant à ce jeu, on gagne une somme $m$ ou on perd une somme $m'$. Quelle relation doit-il exister entre ces deux sommes pour que le jeu soit équitable ?