Autour du nombre d'or

On appelle nombre d'or un rapport de proportionnalité considéré comme harmonieux tant par certains mathématiciens que par certains artistes. On retrouve cette proportion dans les bâtiments du Corbusier, dans des oeuvres musicales contemporaines, voire même dans des tableaux.

On retrouve aussi des manifestations liées au nombre d'or dans la nature, dans les écailles de la pomme de pin ou les graines du tournesol.

Si la dimension "divine" de ce nombre ou son omniprésence restent encore à prouver, nous allons nous concentrer sur les origines et curiosités mathématiques qui entourent ce nombre si particulier.

Calculer le nombre d'or

Euclide définit dans son ouvrage Les Eléments ce qu'il appelle la proportion d'or :

"Une droite est dite coupée en extrême et moyenne raison quand, comme elle est tout entière relativement au plus grand segment, ainsi est le plus grand relativement au plus petit."

1. Pour évoquer un découpage harmonieux d'une longueur, Euclide dit qu'elle est "coupée en extrême et moyenne raison". On note $a$ et $b$ les deux longueurs résultantes de ce découpage, avec $a \lt b$.

   Exprimer mathématiquement le rapport traduisant "[la longueur] tout entière relativement au plus grand segment" et équivalent au "plus grand relativement au plus petit".

On cherche à exprimer le rapport $\displaystyle \frac{a+b}{b} = \frac{b}{a}$.

On peut aussi discuter avec les élèves du terme de "droite" utilisé dans cette citation !

2. On pose $\displaystyle \Phi = \frac{b}{a}$.

   Montrer que, d'après la relation précédente, $\Phi^2 - \Phi - 1 = 0$.

$\displaystyle \frac{b}{a}= \frac{a+b}{b} = \frac{a}{b} + 1$

En posant $\displaystyle \Phi = \frac{b}{a}$, on obtient :

$\displaystyle \Phi = \frac{1}{\Phi} + 1 \iff \Phi^2 = 1 + \Phi$

3. Résoudre l'équation et en déduire la valeur de $\Phi$. C'est ce qu'on appelle le nombre d'or.





On résout l'équation du second degré, dont on ne s'intéresse qu'à la racine positive, puisque $\Phi$ est un rapport entre deux longueurs.

Euclide n'avait pas d'outils mathématiques pour calculer la racine d'une équation du second degré comme nous venons de le faire. L'algèbre n'existait pas encore. En revanche, la définition qu'il donne de cette proportion lui permet d'aboutir à une résolution géométrique, en construisant un "rectangle d'or" dont longueur et largeur vérifient la condition énoncée plus haut.

Avant de revenir sur la construction géométrique de ces rectangles, intéressons-nous au célèbre Fibonacci.

Fibonacci et les lapins

En 1202, un mathématicien italien du nom de Leonardo Fibonacci s'intéresse au problème de la croissance d'une population de lapins. Le problème est le suivant : un couple de lapins donne naissance à un autre couple de lapin aux bout du 2e mois après leur naissance. On part du principe que les lapins se reproduisent chaque mois dès qu'ils le peuvent (donc tous les mois, sauf celui qui a suivi leur naissance), et qu'ils ne meurent jamais. On note $u_n$ le nombre de couples dans l'enclos au bout de $n$ mois (avec $n$ entier naturel).

1. A l'état initial, on considère la naissance d'un seul couple de lapins dans l'enclos, soit $u_0=1$. Au bout du premier mois, les lapins ne peuvent pas se reproduire, on compte toujours un couple : $u_1=1$. Au bout du second, ils se sont reproduits et l'enclos compte maintenant deux couples de lapins : $u_2=2$.

   Combien l'enclos compte-t-il de lapins au bout du troisième mois ? Et du quatrième ?

Le troisième mois, le couple initial de lapin s'est encore reproduit. Le second, en revanche, ne le peut pas. On compte un couple de plus que les deux déjà présents : $u_3=3$.

Le quatrième mois, on compte tous les lapins du mois précédent, auquel on ajoute les lapins du deuxième mois qui se sont reproduits : $u_4 = 3 + 2 = 5$.

2. En déduire une relation entre les termes $u_n$, $u_{n+1}$ et $u_{n+2}$.

$u_{n+2}=u_{n+1}+u_{n}$

3. On appelle la suite $\left(u_n\right)$ la suite de Fibonacci. On souhaite générer en Python une liste des $n$ premiers nombres de cette suite à l'aide d'une fonction liste(n). On placera les valeurs calculées par l'algorithme dans une variable de type liste que l'on appellera fibonacci.

   1. Combien de valeurs initiales sont nécessaires pour calculer les termes de la suite de Fibonacci ? En déduire le nombre de valeurs nécessaires dans la liste fibonacci à l'initialisation et écrire la ligne de code correspondante. On rappelle que les valeurs contenues dans une liste sont à indiquer entre crochets.

   Il faut deux valeurs initiales $u_0$ et $u_1$ afin de calculer les termes de la suite de Fibonacci. Ces deux valeurs doivent se trouver dans la liste lors de l'intialisation. On écrira : fibonacci=[1,1].

   2. On souhaite générer les $n$ premiers termes de la suite. Combien manque-t-il de valeurs dans fibonacci après initialisation ? En déduire le nombre de boucles de calculs à répéter dans le programme.

   A l'initialisation, on a deux valeurs dans la liste. Il en manque donc encore $n-2$. C'est le nombre que l'on indiquera en argument dans la boucle for.

   3. Le calcul à répéter dans la boucle consiste à faire la somme de deux valeurs consécutives de la liste et ajouter cette somme à la suite de cette liste à l'aide de la commande fibonacci.append().

      Pour désigner un terme de celle-ci, on écrira fibonacci[i] avec i le rang du terme dans la liste. Attention toutefois, car le premier terme est toujours désigné par le rang 0.

      Compléter l'extrait d'algorithme suivant :

      for i in range(...):
        u=fibonacci[...]+fibonacci[...]
        fibonacci.append(...)
                  

   4. A l'aide des questions précédentes, écrire la fonction liste(n) qui renvoie la liste des $n$ premiers termes de la suite de Fibonacci.

   def liste(n):
     fibonacci=[1,1]
     for i in range(n-2):
       u=fibonacci[i]+fibonacci[i+1]
       fibonacci.append(u)
     return fibonacci
               

4. On s'intéresse maintenant à la suite $\left(w_n\right)$ définie pour tout $n>0$ telle que $\displaystyle w_n = \frac{u_n}{u_{n-1}}$.

   On souhaite maintenant programmer une fonction quotient(n) qui permettra d'afficher les $n$ premières valeurs de la suite $\left(w_n\right)$. Compléter l'algorithme suivant :

   def quotient(n):
     fibonacci=[... , ...]
     for i in range(n):
       u=fibonacci[...]+fibonacci[...]
       fibonacci.append(...)
     for k in range(...):
       print(fibonacci[...]/fibonacci[...])
           

def quotient(n):
  fibonacci=[1,1]
  for i in range(n):
    u=fibonacci[i]+fibonacci[i+1]
    ibonacci.append(u)
  for k in range(n):
    print(fibonacci[k+1]/fibonacci[k])
        

5. Exécuter quotient(10). Que constate-t-on ?



Les valeurs semblent converger vers un nombre approchant 1,618.

6. On admet que la suite $\left(w_n\right)$ est convergente et on note $l$ sa limite, telle que $\displaystyle l = \lim_{n \to +\infty} w_n = \lim_{n \to +\infty} w_{n+1}$.

   En utilisant la définition de la suite de Fibonacci, montrer que $l$ est solution de l'équation $\displaystyle l = 1 + \frac{1}{l}$.

$\displaystyle l = \lim_{n \to +\infty} w_n = \lim_{n \to +\infty} w_{n+1} = \lim_{n \to +\infty} \frac{u_{n+2}}{u_{n+1}}$

Or, on sait que $u_{n+2}=u_{n+1}+u_{n}$ d'où $\displaystyle l = \lim_{n \to +\infty} \frac{u_{n+2}}{u_{n+1}} = \lim_{n \to +\infty} 1 + \frac{u_{n}}{u_{n+1}}$.

On a vu que $\displaystyle l = \lim_{n \to +\infty} \frac{u_{n+1}}{u_n}$ d'où $\displaystyle l = 1 + \frac{1}{l}$

7. Résoudre l'équation. Que peut-on dire sur la limite de $\left(w_n\right)$ ?

$\displaystyle l = 1 + \frac{1}{l} \iff l^2-l-1=0$

On a vu plus haut les solutions d'une telle équation. La suite $\left(w_n\right)$ tend vers le nombre d'or.

Construction avec le nombre d'or

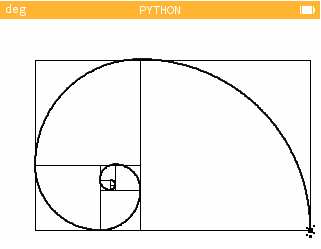
On appelle spirale d'or la construction géométrique d'une spirale logarithmique dont le facteur de croissance est égal au nombre d'or.

Soyons plus clairs : une spirale logarithmique se construit par quart de tour. Cependant, chaque quart de cercle tracé admet un rayon plus grand que le précédent selon un facteur de croissance donné. Ici, il s'agit de notre nombre d'or.

Nous allons tracer une spirale d'or en utilisant les nombres de la suite de Fibonacci comme rayon des cercles dont nous tracerons le quart. Simple, non ? Pas de panique ! Tout d'abord, nous allons créer un nouveau script et importer le module Turtle avec la commande from turtle import * à insérer en tête du programme.

1. Dans un premier temps, nous allons chercher à tracer des rectangles dont les côtés sont des nombres de la suite de Fibonacci. Les rectangles seront positionnés en spirale, comme dans l'exemple ci-dessous.

   

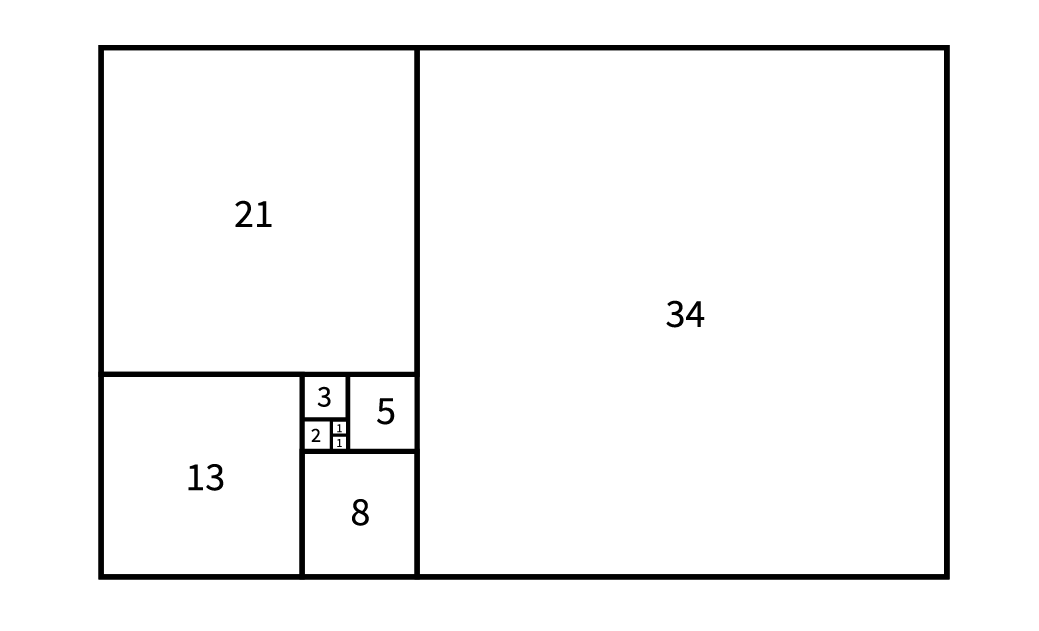
   Quelles sont les lignes de code à inscrire en début de programme afin de générer les sept premiers nombres de la suite de Fibonacci dans une liste fibonacci ?

2. Nous souhaitons maintenant piloter la tortue afin qu'elle trace des carrés de longueur proportionnelle à ces nombres.

   On rappelle que la tortue avance de $x$ pixels avec la commande forward(x) et tourne à droite de $a$ degrés avec la commande right(a)

   D'après le modèle donné ci-contre, quelles sont les instructions à utiliser pour que la tortue trace un premier carré de longueur $l$ et se retrouve en position pour tracer le second (depuis la croix bleue jusqu'à la fin de la 6e étape) ? On pourra optimiser cette série d'instructions avec une boucle.

   

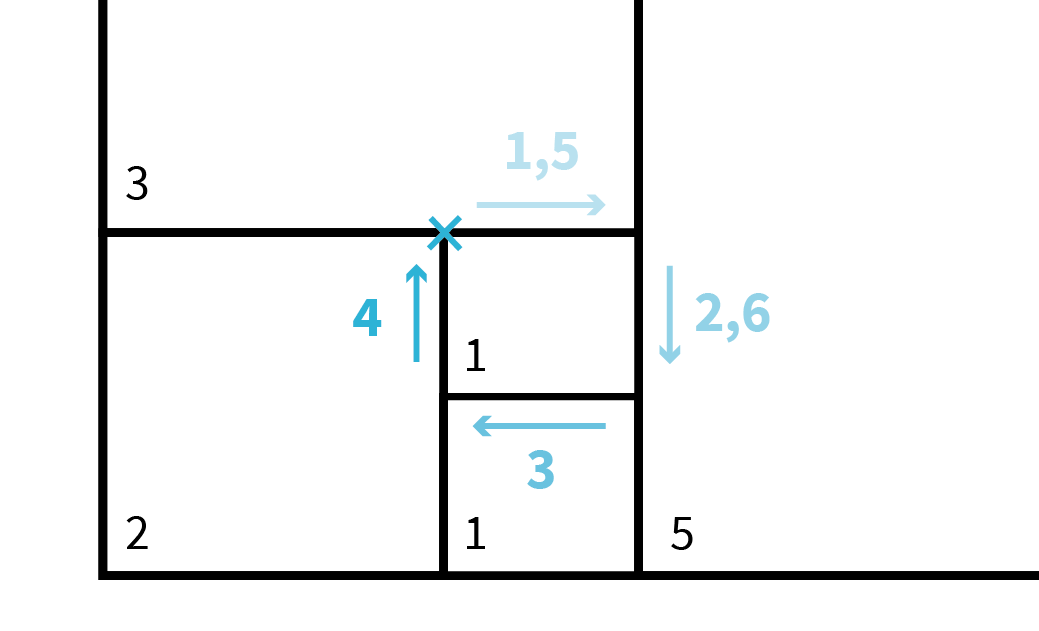
3. On peut parcourir chacun des éléments de la liste fibonacci à l'aide d'une boucle for avec ce type de commande : for number in fibonacci:. Cela signifie qu'à chaque boucle, la variable number équivaut tour à tour à chacun des termes de la liste.

   Comment insérer cette commande avec le bloc d'instructions précédent pour que la longueur de chaque carré dessiné soit proportionnelle (de coefficient 5) à chaque élément de la liste ?

4. Vous disposez maintenant de tous les éléments pour réaliser votre programme. Pour mieux centrer le dessin, on pourra positionner le curseur de départ avec l'instruction goto(x,y), en prenant soin de lever le crayon avec penup() avant le déplacement et en le repositionnant avec pendown().

Pour tracer la spirale, il suffit de retourner au point de départ et d'entrer les lignes de code suivantes :

setheading(0)
for number in fibonacci:
  circle(-number*5,90)
  left(180)
      

A vous de jouer !

from math import *
from turtle import *

penup()
goto(-50,-50)
speed(0)
pendown()
fibonacci=[1,1]
for u in range(7):
  fibonacci.append(fibonacci[u]+fibonacci[u+1])
for number in fibonacci:
  for i in range(5):
    forward(number*5)
    right(90)
  forward(number*5)

penup()
goto(-50,-50)
pendown()
pensize(2)
setheading(0)
for number in fibonacci:
  circle(-number*5,90)
  left(180)