Des histoires de salaire

De l'importance de la négociation

Ugo et Victoria travaillent dans la même entreprise ; cependant, leurs salaires ainsi que les critères d'augmentation de ce salaire diffèrent. En effet, Ugo a commencé à travailler dans l'entreprise avec un salaire de 1600€ brut et son contrat stipule que ce salaire augmentera de 5% tous les ans. Victoria est arrivée en même temps qu'Ugo, mais a démarré avec un salaire de 1800€ avec une promesse d'augmentation de 100€ par an.

1. On appelle $\left( u_n \right)$ la suite associée au salaire de Ugo année après année avec $n$ entier naturel correspondant au nombre d'années d'ancienneté dans l'entreprise.

   De la même façon, $\left( v_n \right)$ est la suite associée au salaire de Victoria au fil des années.

   A quoi correspondent les termes $u_0$ et $v_0$ ? Quelles sont leurs valeurs ?

Les termes $u_0$ et $v_0$ correspondent respectivement aux salaires d'Ugo et de Victoria à leur arrivée dans l'entreprise : $u_0=1600$ et $v_0=1800$.

2. Quels sont les salaires d'Ugo et de Victoria au bout d'un an ? Au bout de deux ans ?

Au bout d'un an, $u_1=1680$ et $v_1=1900$.

Au bout de deux ans, $u_2=1764$ et $v_2=2000$.

3. Exprimer $u_{n+1}$ en fonction de $u_n$ ainsi que $v_{n+1}$ en fonction de $v_n$.

Le salaire d'Ugo augmente de 5% chaque année, d'où $u_{n+1} = 1,05 \times u_n$.

Le salaire de Victoria augmente de 100 euro chaque année, d'où $v_{n+1} = v_n +100.$

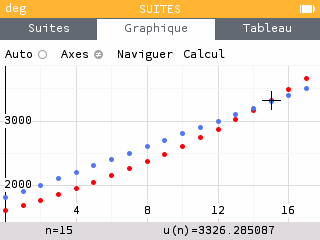
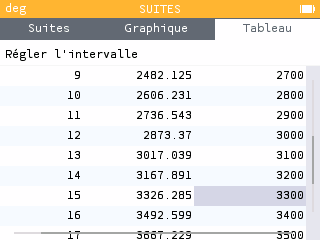
4. A l'aide de la calculatrice, déterminer le nombre d'années au bout duquel le salaire mensuel d'Ugo sera supérieur à celui de Victoria.

   

   

5. 1. A l'aide des questions précédentes, exprimer la formule explicite de chacune des suites.

   La suite $\left( u_n \right)$ est une suite géométrique de raison 1,05 d'où $u_n=1600\times 1,05^n$.

   La suite $\left( v_n \right)$ est une suite arithmétique de raison 100 d'où $v_n=1800+100n$.

   2. Quels seront les salaires cumulés d'Ugo et de Victoria pendant leurs dix premières années dans l'entreprise ? On arrondira le résultat à l'euro.

   Concernant Ugo, nous allons faire la somme des termes $12 \times u_0$ jusqu'à $12 \times u_9$, autrement dit $12 \left( u_0 + u_1 + ... + u_9 \right)$. On utilise la formule de la somme des termes d'une suite géométrique.

   $\displaystyle S = 12 \times 1600 \frac{1-1,05^{10}}{1-1,05} = 241 496$

   Concernant Victoria, nous allons faire la même chose en utilisant la formule de la somme des termes d'une suite arithmétique :

   $\displaystyle S' = 12 \times 10 \times \frac{1800 + 1800+100 \times 9}{2} = 270 000$

Choisir comment placer son argent

Victoria souhaite placer son argent dans une banque mais elle ne sait pas encore laquelle. Elle hésite entre trois banques et souhaite examiner le taux de satisfaction des clients pour chacune d'entre elles. Il lui manque cependant des données. Pouvez-vous l'aider ?

Le taux de satisfaction des clients de ces trois banques est de 95,43%. Ils se répartissent leurs clients comme ceci : 56% sont dans la banque A, 33% dans la banque B et 23% dans la banque C. 16% des clients de la banque A sont mécontents de leur choix tandis que 86% des clients de la banque B en sont ravis.

Quel est le taux de satisfaction des clients de la banque C ?

On notera S l'événement : "le client est satisfait".