Le module kandinsky

Boucle for Listes Module kandinsky

Objectif

Cette fiche présente le module graphique Kandinsky de la calculatrice NumWorks sur quelques exemples faciles à mettre en place.

Cet exercice ainsi que sa correction est proposé par Philippe Moutou. Il enseigne au lycée Henri IV à Paris.

Le module graphique Kandinsky est présent dans la calculatrice NumWorks, de même que les modules math (fonctions mathématiques usuelles), cmath (nombres complexes) et random (nombres aléatoires). La particularité de ce module est d'être une invention de NumWorks : ce module n'est pas proposé par les distributions habituelles de Python qui propose par exemple à sa place le module Tkinter. Dans ce module, il y a quatre fonctions : color, get_pixel, set_pixel et draw_string.

Changer la couleur d'un pixel

L'écran de la calculatrice est composé de 320 pixels sur sa longueur et de 222 pixels sur sa hauteur, ce qui fait 71040 pixels en tout. On peut fixer la couleur de chacun de ces pixels en exécutant l'instruction set_pixel(x,y,color). Pour cela, il suffit d'indiquer :

les coordonnées (x,y) du pixel ;
la couleur color(r,g,b).

La couleur est définie selon le système rouge, vert, bleu (rgb = red, green, blue) qui nécessite d'indiquer une valeur entière comprise entre 0 et 255 pour chacun des trois paramètres. Si on indique color(255,0,0) on obtient un rouge pur, pour un gris clair, ce sera par exemple color(150,150,150) et un pourpre color(158,14,64). Le noir est color(0,0,0) et le blanc, à l'opposé, est color(255,255,255).

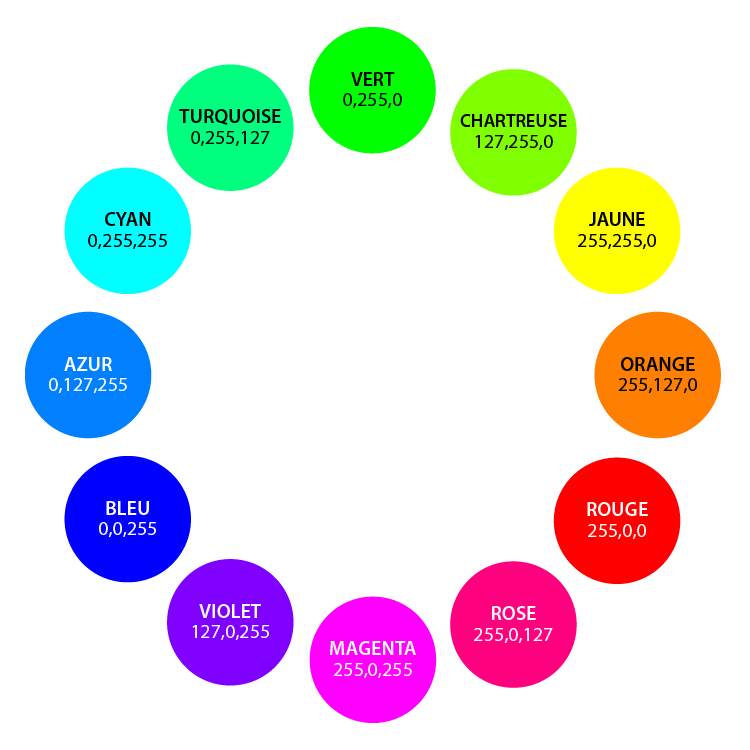
Le cercle chromatique ci-contre donne davantage d'exemples mais pour une nomenclature plus complète, consulter cette page ou bien une des innombrables applications donnant les codes couleur.

Avec ces deux premières instructions, il est donc possible de dessiner à peu près ce qu'on veut, de la couleur qu'on veut. Il suffit de dire quels pixels colorer et comment.

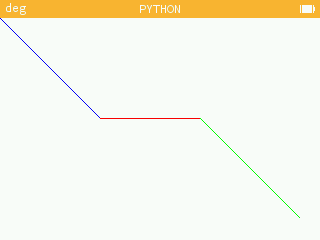
Pour tracer la ligne brisée de l'illustration, j'ai écrit le programme suivant :

from kandinsky import *
for i in range(100):
  set_pixel(i,i,color(0,0,255))
  set_pixel(i+100,100,color(255,0,0))
  set_pixel(i+200,i+100,color(0,255,0))

Écrire un texte

L'instruction draw_string(texte,x,y) permet d'écrire un texte dans l'image, toujours en noir sur fond blanc, la taille et la police des caractères étant immuables. C'est minimaliste, ce qui n'a pas que des inconvénients.

Le rectangle dans lequel est inscrit le texte est repéré par les coordonnées de son sommet supérieur gauche. Dans l'image ci-contre, j'ai tracé un + pour indiquer le point de coordonnées (100,100) mais j'ai dû écrire le texte des coordonnées en le décalant pour ne pas qu'il chevauche le dessin du + : son sommet supérieur gauche a, ici, les coordonnées (110,110).

Capturer la couleur d'un pixel

L'instruction get_pixel(x,y) renvoie la couleur du pixel situé aux coordonnées (x,y).J'essaie c=get_pixel(0,0) et écrit sur l'écran la conversion de c en chaîne de caractères (on ne dispose plus de la console dès lors qu'un pixel a été allumé). J'obtiens un nombre ! Si la couleur est (0,0,255) j'obtiens 31, avec (0,255,0) j'obtiens 2016 et avec (255,0,0) j'obtiens 63488. Le nombre varie entre 0 (noir) et 65535 (blanc). Je m'aperçois que get_pixel(x,y) renvoie un nombre. Je peux lui ajouter un autre nombre et employer le résultat comme couleur, je peux même déclarer une couleur avec un tel nombre. Par exemple, si c=63488, l'instruction set_pixel(0,0,c) est correcte. Pour faire du blanc, je peux partir d'un jaune 65504 qui correspond à (255,255,0) et lui ajouter le bleu intense 31, ce qui donne 65535. Retrouver les composantes rgb à partir du nombre n obtenu par get_pixel est assez technique, mais il faut noter que les 256 valeurs de l'intensité d'une couleur ne sont pas différentes : de 0 à 7 l'intensité vaut 0, de 8 à 15 elle vaut 1, ainsi de suite jusqu'aux valeurs de 248 à 255 où l'intensité vaut 31. Il n'y a donc que 32 intensités différentes pour chacune des trois composantes.

Exercice

Écrire un programme qui réalise un dégradé horizontal entre deux couleurs quelconques.

L'idée ici est de couvrir l'écran avec des pixels dont la couleur est identique sur une même colonne verticale ( $x$ constant) mais change sur les lignes horizontales ( $y$ constant), passant progressivement de c1 à gauche à c2 à droite. Pour obtenir le dégradé, on calcule les différences dr, dg et db entre les composantes rgb de c2 et c1 et on ajoute aux composantes de c1 la part de ces différences correspondant à l'avancement dans la ligne (donc au numéro de la colonne).

from kandinsky import *
def couleur():
  dr=c2[0]-c1[0]
  dg=c2[1]-c1[1]
  db=c2[2]-c1[2]
  return color(c1[0]+i*dr//320,c1[1]+i*dg//320,c1[2]+i*db//320)

c1=(255,255,0)
c2=(255,0,255)
for i in range(320):
  col=couleur()
  for j in range(222):
    set_pixel(i,j,col)

Voici le résultat pour un dégradé entre le jaune et le magenta :

Pour prolonger cette idée, puisque la hauteur de l'écran n'est pas utilisée ici (sauf pour étaler la couleur), je vais dégrader verticalement la couleur d'une colonne entre sa valeur actuelle qui sera appliquée sur la ligne du haut et une troisième couleur (pour compléter mon exemple, je prendrai du cyan) qui ne sera atteinte que sur la ligne du bas. J'applique exactement le même principe que précédemment, calculant dans un premier temps la couleur du haut (dégradé entre c1 et c2) dans les variables r, g et b et, dans un second temps, dégradant la couleur obtenue avec c3.

from kandinsky import *
def couleur():
  r=c1[0]+i*(c2[0]-c1[0])//320
  g=c1[1]+i*(c2[1]-c1[1])//320
  b=c1[2]+i*(c2[2]-c1[2])//320
  r+=j*(c3[0]-r)//320
  g+=j*(c3[1]-g)//320
  b+=j*(c3[2]-b)//320
  return color(r,g,b)

c1=(255,255,0)
c2=(255,0,255)
c3=(0,255,255)
for i in range(320):
  for j in range(222):
    col=couleur()
    set_pixel(i,j,col)

Autre exercice

Écrire un programme qui place des points aléatoirement dans l'écran, la couleur de ces points étant fonction de la distance au centre de l'écran, le point de coordonnées (160,111).

from kandinsky import *
from random import *
from math import *

def couleur(x,y):
  d=int(sqrt((x-160)**2+(y-111)**2)/16.25)
  return color(c[d][0],c[d][1],c[d][2])

def tirage(n):
  for i in range(n):
    x=randint(0,320)
    y=randint(0,222)
    c=couleur(x,y)
    set_pixel(x,y,c)
    set_pixel(x+1,y,c)
    set_pixel(x,y+1,c)
    set_pixel(x+1,y+1,c)

c=[[255,0,0],[255,127,0],[255,255,0],[127,255,0],[0,255,0],[0,255,127],[0,255,255],[0,127,255],[0,0,255],[127,0,255],[255,0,255],[255,0,127]]

Le programme détermine si la couleur du point appartient à l'une des douze couleurs de notre cercle chromatique. La distance maximum au centre de l'écran étant 195 environ, la division par 16.25 permet de ramener les coordonnées aléatoires à l'une de ces douze couleurs. J'ai dessiné des points plus gros, formés de quatre pixels, pour qu'ils soient plus visibles.

Essai pour tirage(5000) :

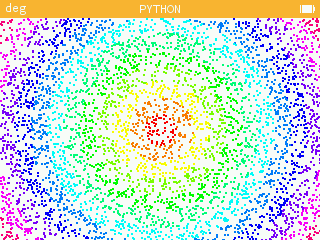
Essai pour tirage(50000) :

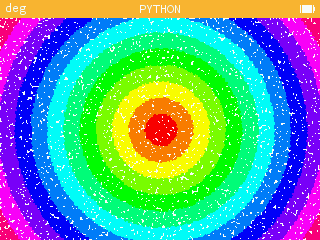
Tirage pseudo-aléatoire de 50000 points.

Pour prolonger ce travail, on peut obtenir un passage progressif d'une couleur à l'autre, un dégradé sans frontière : éliminons les six couleurs intermédiaires qui sont seulement les milieux des dégradés successifs et adaptons le module qui permettait d'obtenir un dégradé dans l'exercice précédent. Le résultat est alors un peu différent.

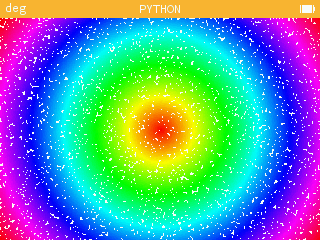
from kandinsky import *
from random import *
from math import *

def degrade(c1,c2,k):
  dr=c2[0]-c1[0]
  dg=c2[1]-c1[1]
  db=c2[2]-c1[2]
  return color(c1[0]+int(k*dr),c1[1]+int(k*dg),c1[2]+int(k*db))

def tirage(n):
  for i in range(n):
    x=randint(0,320)
    y=randint(0,222)
    c=couleur(x,y)
    set_pixel(x,y,c)
    set_pixel(x+1,y,c)
    set_pixel(x,y+1,c)
    set_pixel(x+1,y+1,c)

def couleur(x,y):
  d=sqrt((x-160)**2+(y-111)**2)/32.5
  return degrade(c[int(d)],c[(int(d)+1)%6],d-int(d))

c=[[255,0,0],[255,255,0],[0,255,0],[0,255,255],[0,0,255],[255,0,255]]