Dessin d'une rosace

Instruction conditionnelle Boucle for Module kandinsky

Objectif

Dessin de trois rosaces grâce au module kandinsky. Le résultat de l'exercice Dessin d'un cercle sera utilisé.

Cet exercice ainsi que sa correction est proposé par Philippe Moutou. Il enseigne au lycée Henri IV à Paris.

Exercice

Écrire un programme qui trace une de ces rosaces qui ne sont constituées que de cercles (les deux premières sont classiques et la troisième, trouvée sur internet, est appelée spirale de Georgia).

Corrigé

La première de ces rosaces est la plus simple des trois avec son rayon et sa couleur constants. Je vais mettre le nombre de cercles tracés en paramètres: l'idée est de tracer $n$ cercles de rayon $r$ , les centres de ces cercles étant régulièrement disposés sur un cercle de centre $O(160,111)$ – le centre de l'écran – et de rayon $r$ . On va réutiliser une nouvelle fois notre fonction cercle (voir la fiche "Dessin d'un cercle") et calculer les coordonnées de chaque centre en appliquant une rotation de centre $O$ et d'angle $\displaystyle\frac{2\pi}{n}$ . Le résultat est tout de suite satisfaisant.

from kandinsky import *
from math import *
def cercle1(x0,y0,r,c,e):
  for i in range(2*e):
    xd=x0-int((r-i*0.5)/sqrt(2))
    xf=x0+int((r-i*0.5)/sqrt(2))
    for x in range(xd,xf+1):
      x1=x
      y1=y0+int(sqrt((r-i*0.5)**2-(x-x0)**2))
      set_pixel(x,y1,c)
      for j in range(3):
        x2=x0+y1-y0
        y2=y0+x0-x1
        set_pixel(x2,y2,c)
        x1,y1=x2,y2

def rosace(n,r,c,e):
  x,y=160+r,111
  for i in range(n):
    x1=int(160+r*cos(i*2*pi/n))
    y1=int(111+r*sin(i*2*pi/n))
    cercle(x1,y1,r,c,e)

cint=color(205,50,123)
cbor=color(0,0,0)
rosace(12,50,cint,1)

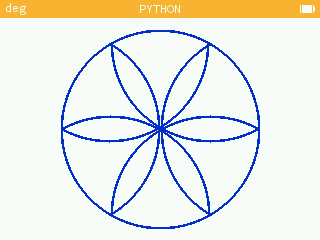
Pour obtenir la deuxième rosace, on peut se contenter de glisser dans la fonction rosace un test qui examine si le point à tracer est à l'intérieur du cercle de centre $O$ et de rayon $r$ (le cercle sur lequel sont placés les centres des arcs que l'on souhaite garder). En implémentant cette méthode rosace1, je m'aperçois que la rosace obtenue a des pétales entiers pour $n=3, 6, 9, 12, ..., 18, 24, 30$ , soit les multiples de 3, et les pétales sont tronqués pour les autres valeurs de $n$ .

Rosace intermédiaire avec test d'inclusion.

from kandinsky import *
from math import *

def cercle1(x0,y0,r,c,e):
  for i in range(2*e):
    xd=x0-int((r-i*0.5)/sqrt(2))
    xf=x0+int((r-i*0.5)/sqrt(2))
    for x in range(xd,xf+1):
      x1=x
      y1=y0+int(sqrt((r-i*0.5)**2-(x-x0)**2))
      if sqrt((160-x1)**2+(111-y1)**2)<r:
        set_pixel(x1,y1,c)
      for j in range(3):
        x2=x0+y1-y0
        y2=y0+x0-x1
        if sqrt((160-x2)**2+(111-y2)**2)<r:
          set_pixel(x2,y2,c)
        x1,y1=x2,y2

def rosace1(n,r,c,e):
  x,y=160+r,111
  for i in range(n):
    x1=int(160+r*cos(i*2*pi/n))
    y1=int(111+r*sin(i*2*pi/n))
    cercle1(x1,y1,r,c,e)
  cercle1(160,111,r,c,e)

cint=color(5,50,200)
cbor=color(0,0,0)
rosace1(6,100,cint,2)

La dernière rosace est plus complexe que les autres avec ses changements de couleur et de rayon.

from kandinsky import *
from math import *

def cercle2(x0,y0,r,c,e):
  for i in range(2*e):
    xd=x0-int((r-i*0.5)/sqrt(2))
    xf=x0+int((r-i*0.5)/sqrt(2))
    for x in range(xd,xf+1):
      x1=x
      y1=y0+int(sqrt((r-i*0.5)**2-(x-x0)**2))
      set_pixel(x,y1,c)
      for j in range(3):
        x2=x0+y1-y0
        y2=y0+x0-x1
        set_pixel(x2,y2,c)
        x1,y1=x2,y2

def rosace3(n,r,c1,c2,e):
  rj=r
  for j in range(n-2):
    rj=int(rj-rj/n)
    for i in range(n):
      x1=int(160+rj*cos(i*2*pi/n))
      y1=int(111+rj*sin(i*2*pi/n))
      if j==0 or j>n-4:
        col=c2
      else:
        col=c1
      cercle2(x1,y1,rj,col,e)

col1=color(5,50,120)
col2=color(255,25,25)
rosace3(10,55,col1,col2,1)