Cryptographie
Division euclidienne Nombres premiers Pourcentages Programmation Python
Objectif
L'objectif de cette activité est d'amener quelques notions d'arithmétique autour de la cryptographie. Un prolongement en programmation Python est possible.
Chiffre de César
On dit que César cryptait ses messages afin de les rendre incompréhensibles si quelqu'un venait à les intercepter. Sa méthode était simple : il décalait les lettres de trois rangs. Ainsi, la lettre A était associée à un D, la lettre B au E et ainsi de suite. Bien sûr, pour crypter les trois dernières lettres, il suffisait de recommencer l'alphabet.
-
On note le rang de la lettre à crypter (on propose d'associer la lettre A au nombre 0 pour plus de simplicité) et le rang de la lettre chiffrée. Proposer une formulation afin d'exprimer la relation entre et .
-
Le code de César est un mode de chiffrement affine. A chaque lettre est associée une autre selon une relation mathématique de type , et étant les rangs associés à ces lettres (ou plus précisément, le rang de la lettre après cryptage correspond au reste de dans la division euclidienne par 26).
On considère dans un premier temps que .
-
On propose d'utiliser . Qu'en pensez-vous ?
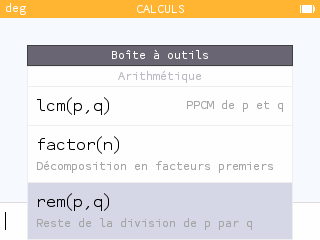
On pourra utiliser une fonction de la calculatrice pour calculer plus rapidement le reste d'une division euclidienne : Boîte à outils > Arithmétique.

-
Quelle condition faut-il respecter pour que et ne soient pas associés au même rang, c'est-à-dire qu'une lettre ne puisse pas être codée par elle-même ?
-
On considère maintenant que est un réel non-nul.
-
On propose de crypter un message à l'aide de la relation . Que constate-t-on ?
-
On veut que chaque lettre soit codée de manière différente. C'est-à-dire que pour chaque lettre de l'alphabet de l'ensemble de départ, on veut associer une lettre de l'alphabet dans l'ensemble d'arrivée de sorte à ce qu'elles soient toutes utilisées. Chaque lettre codée n'aura pour antécédent qu'une seule autre lettre. C'est ce que l'on appelle une bijection.
Pour respecter cette condition, il faut que le coefficient soit premier avec le nombre de lettres utilisées. Proposer un type de chiffrement affine qui vérifie cette condition.
-
On propose de crypter le mot MATH en utilisant une fonction définie telle que pour tout compris entre 0 et 25, correspondant au rang de la lettre de départ, on associe . Le reste de la division euclidienne de par 26 donne le rang de la lettre chiffrée. Comment est crypté le mot MATH ?
Les élèves vont bien sûr proposer mais la relation n'est pas satisfaisante pour les lettres X, Y et Z.
et sont liés par une fonction telle que pour tout compris entre 0 et 25, est le reste de la division euclidienne de par 26.
On peut pourquoi pas aborder la notion de congruence et de modulo avec les élèves : .
On peut aussi proposer aux élèves de réaliser un petit programme en Python pour coder facilement un texte. Il nécessite toutefois des fonctions avancées et la manipulation des chaînes de caractères. Un script est disponible ici.
Avec ce mode de chiffrement, les lettres sont codées par elles-mêmes. Par exemple, la lettre de rang 4 sera codée par , dont le reste dans la division euclidienne par 26 est 4. Ce chiffre n'est pas satisfaisant car il ne code rien !
Si et sont associés à la même lettre, alors et ont le même reste dans la division par 26.
D'où avec entier naturel.
Or, , donc 26 doit diviser et 26 doit diviser .Il faut donc choisir le nombre tel que 26 ne divise pas .
Dans la question précédente, : 26 divise donc et la lettre est codée par elle-même.
Avec ce type de cryptage, on remarque que deux lettres distinctes peuvent être codées par une même lettre. Par exemple, le A et le N sont codés tout deux par la lettre B.
On peut utiliser l'application Statistiques pour calculer plus rapidement les valeurs des rangs après chiffrage. En V1, on entre manuellement les nombres de 0 à 25. En N1 on entre avec une formule (après avoir sélectionné le titre de la colonne) les résultats de l'équation en utilisant x = V1. Dans une troisième colonne, on entre avec une formule le reste de la division euclidienne de la colonne N1 par 26.
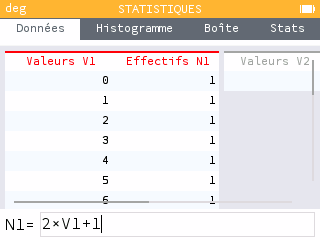
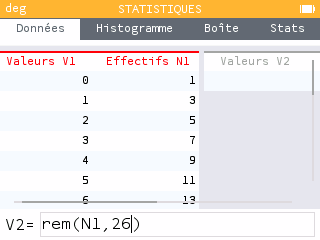
Ce type de chiffre risque de créer beaucoup de confusions pour le destinataire qui souhaiterait le décoder !
Il y a 26 lettres dans l'alphabet. Pour choisir , il faut donc éliminer tous les nombres pairs, ainsi que 13, 26 et leurs multiples.
La lettre M est associée à dont l'image par la fonction est 96. Le reste de la division euclidienne de 96 par 26 est 18, ce qui correspond à la lettre S.
La lettre A est associée à dont l'image par la fonction est 12, ce qui correspond à la lettre M.
La lettre T est associée à dont l'image par la fonction f est 145. Le reste de la division euclidienne de 145 par 26 est 15, ce qui correspond à la lettre P.
La lettre H est associée à dont l'image par la fonction est 61. Le reste de la division euclidienne de 61 par 26 est 9, ce qui correspond à la lettre J.
Le mot MATH se code SMPJ.
Pour aller plus loin !
Pour augmenter d'un cran la sécurité de notre cryptage, il est possible de procéder à un cryptage en utilisant une clé, sous forme d'un mot. C'est la clé qui va déterminer la substitution nécessaire. Prenons un exemple.
On souhaite toujours crypter le mot MATH mais cette fois-ci, nous allons utiliser une clé : CHAT. Le cryptage de la lettre M se fait à l'aide de la lettre C, de rang 2, ce qui détermine le nombre de décalage à effectuer : la lettre M devient O. De la même façon, la lettre A est cryptée par un H, de rang 7 : elle devient elle-même un H. La lettre T est cryptée par la lettre A, de rang 0 : il n'y a pas de décalage, le T reste un T. Enfin, la lettre H est cryptée par un T, de rang 19 : elle devient un A.
Le mot MATH se code OHTA.
Ce type de chiffrement est appelé chiffre de Vigenère, du nom de son génial inventeur. Pour coder ou décoder plus rapidement un message en suivant ce principe, on peut se référer à la table de Vigenère, qui se trouve facilement sur Internet.
Décrypter par analyse fréquentielle
Dans la langue française, certaines lettres sont beaucoup plus courantes que d'autres. Par exemple, la lettre "E" est de loin l'une des plus utilisées.
Il est possible de calculer approximativement la fréquence d'apparition de chacune des lettres dans notre langue à partir d'une grande quantité de texte. Cette fréquence peut ensuite être utilisée pour déchiffrer un texte chiffré par substitution.
Wikipédia nous donne le tableau suivant (les valeurs sont données en pourcentage) pour la langue française :
| A | B | C | D | E | F | G | H | I | J | K | L | M |
| 8,20 | 0,90 | 3,35 | 3,67 | 16,72 | 1,07 | 0,87 | 0,74 | 7,58 | 0,61 | 0,07 | 5,46 | 2,97 |
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 7,10 | 5,84 | 2,52 | 1,36 | 6,69 | 7,95 | 7,24 | 6,43 | 1,84 | 0,05 | 0,43 | 0,13 | 0,33 |
-
Combien de fois, en moyenne, apparaît la lettre E, dans une page de 2500 caractères ?
-
On souhaite décrypter un texte codé. Calculer la fréquence d'apparition de chacune des lettres dans ce texte codé puis décoder le texte en proposant des pistes d'amélioration de la méthode par analyse fréquentielle.
La machine est quelquefois plus fiable que l'humain ! Aussi pour calculer les fréquences, on propose de programmer un script en Python. On pourra notamment utiliser l'instruction count() qui permet de compter le nombre d'occurence dans une chaîne de caractères. Par exemple, si 'message' contient une chaîne de caractères, l'instruction message.count(ma) comptera le nombre d'occurences de "ma" dans cette chaîne.
Voici le texte à décoder :
LOI SMPJOSMPQUWOI IGZP WZ OZIOSTLO HO AGZZMQIIMZAOI MTIPBMQPOI BOIWLPMZP HO BMQIGZZOSOZPI LGCQUWOI MNNLQUWOI M HOI GTXOPI HQDOBI OLI UWO LOI OZIOSTLOI SMPJOSMPQUWOI, LOI ZGSTBOI, LOI VGBSOI… SOBAQ KQEQNOHQM !
D'après le tableau précédent, la lettre E apparaît en moyenne avec une fréquence de 16,72% dans la langue française. Dans un texte de 2500 caractères, cela représente environ apparitions de la lettre E dans la page.
Un script est disponible à cette adresse.
Décrypter ce texte paraît impossible avec l'aide seulement de l'analyse fréquentielle. Le texte est trop court. On peut cependant formuler des hypothèses en étudiant l'ordre et les groupes de lettres.
Les lettres O et I sont largement les plus présentes dans ce texte. On peut raisonnablement penser que l'une d'elles est initialement la lettre E. De plus, elles se suivent souvent dans cet ordre. On les retrouve notamment dans le groupe de trois lettres "LOI" qui revient régulièrement. On aboutit à la conclusion que le E est sans doute codé par le O et que le I code donc un S (qui est la troisième lettre la plus présente dans la langue française d'après le tableau initial).
La lettre A est la seconde lettre la plus fréquente dans la langue française. Dans notre texte crypté, les lettres M et P et Q sont les lettres suivantes les plus fréquentes. On peut poser l'hypothèse que la lettre A est codée par l'une ou l'autre. Or, la lettre P est souvent en fin de mot, il ne peut donc pas s'agir de la lettre A.
Et ainsi de suite pour décoder la totalité du texte.
La ponctuation et les apostrophes peuvent aussi être de bonnes pistes pour identifier certaines lettres ! L'analyse fréquentielle est intéressante, mais ne suffit pas toujours. L'utilisation de certains anglicismes peut par exemple faire augmenter rapidement la fréquence de certains caractères plutôt rares en français, comme c'est le cas ici.
Voici le texte original :
"Les mathématiques sont un ensemble de connaissances abstraites résultant de raisonnements logiques appliqués à des objets divers tels que les ensembles mathématiques, les nombres, les formes… Merci Wikipédia !"