Jouer au franc-carreau

Le principe de ce jeu datant du Moyen-Âge est extrêmement simple : on lance une pièce sur un carrelage. Si la pièce ne touche aucun des bords, elle est à franc-carreau et l'on considère que c'est gagné. Une pièce qui atterrit en dehors du carrelage doit être relancée tandis qu'une pièce qui touche les lignes du carrelage est bien sûr perdue.

On propose de dessiner une grille régulière sur une feuille de papier et de lancer dix fois la même pièce sur la grille. Aucune valeur n'est imposée concernant la dimension des carreaux ou de la pièce.

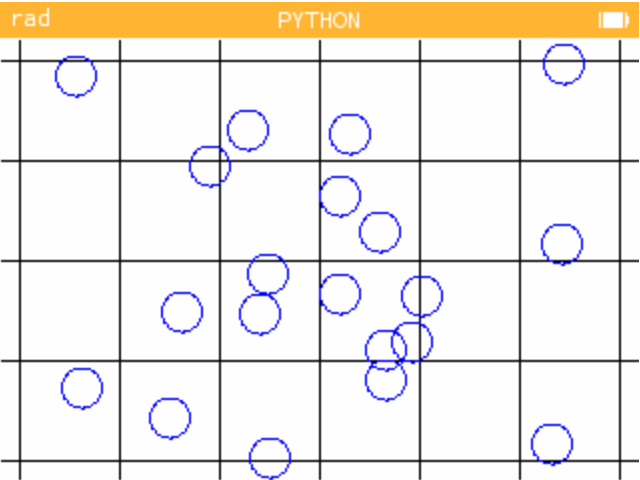
Quelle est la fréquence de francs-carreaux que vous avez réalisés ?

Quelles sont vos premières réactions par rapport à ce jeu ?

On propose de procéder à dix nouveaux essais, avec la même grille et la même pièce. La fréquence de pièces franc-carreaux est-elle différente ? Pourquoi ?

Modéliser le jeu du franc-carreau en Python

Afin de pouvoir réaliser l'expérience à grande échelle et avoir la possibilité de faire varier les différentes variables de notre jeu, comme la dimension des carreaux ou de la pièce, on propose de le programmer en Python.

On utilisera dans un premier temps le module Turtle de la calculatrice afin d'obtenir un visuel du jeu. Dans un nouveau script, on importe le module Turtle à l'aide de la commande from turtle import *, que l'on peut trouver dans la boîte à outils toolbox.

Le module Turtle permet de déplacer une tortue à l'écran. Imaginons qu'un crayon soit attaché à notre tortue : elle laisse une trace derrière elle au fil de ses déplacements. On peut demander à notre tortue de relever son crayon avec penup() et de l'abaisser avec pendown() afin de contrôler les traces qu'elle laisse derrière elle.

1. Dans un premier temps, on cherche à dessiner la grille sur l'écran de la calculatrice au moyen d'une fonction grille().

   Dessiner une ligne verticale et une ligne horizontale en utilisant les commandes : goto(x;y) qui permet de se rendre au point de coordonnées (x;y), forward(l) qui fait avancer la tortue de $l$ pixels, setheading(a) qui oriente la tortue de $a$ degrés en suivant l'orientation du cercle trigonométrique. Toutes ces commandes peuvent être écrites en toutes lettres, ou bien se trouvent dans la boîte à outils, dans le menu du module Turtle.

   Pour information, l'écran de la calculatrice fait 320 pixels de largeur et 222 pixels de hauteur, le centre de l'écran admettant des coordonnées (0;0).

   


2. On propose maintenant d'utiliser des boucles et des fonctions pour réduire le nombre de lignes à écrire pour notre programme.

   1. Compléter le programme pour qu'il dessine une grille avec des carreaux carrés de côté $l$ :

   from math import *
   from turtle import *
   
   def ligne(l):
     pendown()
     forward(l)
     penup()
   
   def grille(l):
     penup()
     for i in range(-150,160,l):
       goto(i,111)
       setheading(-90)
       ligne(l)
     for j in range(-100,110,l):
       goto(-160,j)
       setheading(0)
       ligne(l)
           

   2. D'après ce programme, comment sont positionnées les lignes horizontales et verticales ?

   A l'horizontale comme à la verticale, la première ligne est située à environ 10 px du bord de l'écran, et les suivantes sont positionnées $l$ pixels plus loin.

   On trace d'abord les lignes à la verticale, de haut en bas en commençant par la gauche, puis les lignes horizontales, de gauche à droite en commençant par le bas.

   3. Quelle commande faut-il entrer dans la console pour obtenir une grille avec des carreaux de côté 50 px ?

   On lancera grille(50).

3. On souhaite réaliser une fonction piece(r) permettant de dessiner un cercle de rayon $r$ à des coordonnées déterminées au hasard.

   On propose donc de rajouter en tête du script la commande from random import *, afin de pouvoir utiliser la fonction randint(a,b) permettant de générer aléatoirement un entier compris entre a et b. On pourra ainsi envoyer la tortue sur des coordonnées déterminées au hasard. On rappelle que l'écran de la calculatrice fait 320 pixels de largeur et 222 pixels de hauteur, le centre de l'écran admettant des coordonnées (0;0).

   Pour dessiner la pièce, on utilisera simplement la fonction circle(r) du module Turtle.

   Ecrire la fonction piece(r). On pourra vérifier la validité du script en testant dans la console.

On propose le script suivant :

def piece(r):
  penup()
  goto(randint(-130,130),randint(-110,90))
  pendown()
  circle(r)
    

On a réduit volontairement le range des coordonnées afin de s'assurer que la pièce soit bien dessinée à l'intérieur de notre écran. Les coordonnées définies par la fonction aléatoire correspondent au point le plus bas du cercle, d'où l'utilisation d'un range sur l'axe des ordonnées qui ne va pas jusqu'en haut de l'écran.

4. Il ne nous reste plus qu'à lancer notre jeu. On propose de garder le contrôle sur la taille de l'échantillon, la dimension des carreaux et la dimension de la pièce, à l'aide de la fonction suivante :

   def jeu(n,l,r):
     grille(l)
     for i in range(n):
       piece(r)
     hideturtle()
       

   Il est possible de modifier les couleurs ou les vitesses de tracé relatives à chacun des éléments de notre modélisation. Un script se trouve en ligne à cette adresse.

   Quelle est la signification de chacune des variables de cette fonction ?

n est le nombre de pièces lancées, l est la dimension d'un carreau et r est le rayon d'une pièce.

5. Lancer jeu(10,50,10). Quelle est la fréquence de pièces en franc-carreau ? Lancer dix fois la simulation. Quelle est la moyenne des résultats obtenus ? Comparer votre résultat à celui de vos camarades.

On peut à nouveau discuter de la fluctuation des résultats avec les élèves et poser des hypothèses sur la probabilité que la pièce soit franc-carreau. Les élèves proposeront sans doute d'enlever les valeurs extrêmes, ou de réaliser une moyenne sur les résultats de chacun. On peut aborder la notion d'intervalle de confiance si ce n'est pas déjà fait.

Calculer la probabilité d'une pièce franc-carreau

On s'intéresse maintenant à notre jeu sous l'angle mathématique.

1. Quels sont les paramètres susceptibles de faire augmenter la probabilité qu'une pièce soit franc-carreau ? Quelle est alors la grandeur mathématique mise en cause dans ces paramètres ?

La probabilité sera plus élevée si on augmente les dimensions du carreau, ou si l'on diminue celle de la pièce. C'est donc l'aire qui est impliquée dans le calcul de cette probabilité.

2. On reste dans la situation où l'on lance une pièce de 10 px (ou 1 cm) de rayon, sur des carreaux de 50 px (ou 5 cm).

   Prenons l'exemple d'un seul carreau. On s'intéresse au centre O de la pièce qui est lancée dans celui-ci. Pour quelles positions de O, la pièce touche-t-elle un bord du carreau ?

Si le centre O de la pièce est situé à moins de 10 px (ou 1 cm) du bord, alors celle-ci touchera forcément l'une des lignes du carreau.

3. En déduire les positions de O pour lesquelles la pièce est franc carreau.

La pièce est donc franc-carreau si son centre se situe à plus 10 px (ou 1 cm) d'un bord. Il faut donc enlever une bordure de 10 px de largeur tout autour du carreau.

4. On admet que la probabilité d'atteindre une zone est proportionnelle à l'aire de cette zone. Quelle est la probabilité pour que la pièce soit franc-carreau ? Comparer ce résultat à la fréquence observée dans la partie 2.

Les positions favorables pour O se situent dans une surface de 30 px de côté (la longueur d'un carreau à laquelle on soustrait, de part et d'autre, le rayon d'une pièce), tandis que l'ensemble des positions possibles correspond à la surface du carreau.

On en conclut que $\displaystyle p=\frac{30 \times 30}{50 \times 50} = \frac{9}{25}$.

On peut comparer ce résultat à la fréquence obtenue dans la partie 2, et même à l'intervalle de confiance s'il a été calculé dans cette partie.

Essayez d'appliquer vos calculs à d'autres dimensions de carreau ou de pièce, et confrontez-les à l'expérience grâce à votre script !