Le théorème de Pythagore par Garfield

Géométrie

Objectif

Courte activité géométrique pour la semaine des mathématiques !

On connaît plusieurs dizaines de démonstrations du théorème de Pythagore. On propose de s'intéresser à l'une de ces démonstrations, simple et efficace, dont l'auteur est un mathématicien devenu par la suite président des Etats-Unis d'Amérique en 1881 : James A. Garfield !

Tous les triangles de la figure sont rectangles.

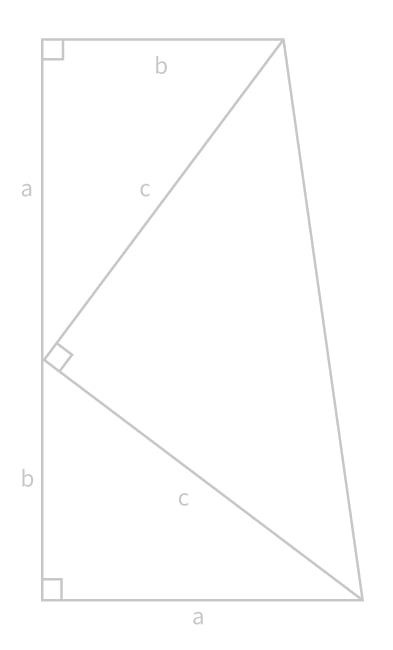
Le principe est ici très simple : il suffit de calculer l'aire du trapèze de deux façons différentes, puis d'en conclure une égalité entre les côtés $a$ , $b$ et $c$ .

On redonne la formule de l'aire d'un trapèze : $\displaystyle \mathscr{A}=\frac{1}{2}\left(b+\mathscr{B}\right) h$

A vous de jouer !

D'une part, on utilise la formule de l'aire du trapèze afin de calculer la surface : $\displaystyle \mathscr{A}=\frac{1}{2}\left(a+b\right)^2$ .

D'autre part, on fait la somme des trois triangles rectangles : $\displaystyle \mathscr{A}=\frac{ab}{2}+\frac{ab}{2}+\frac{c^2}{2}=\frac{1}{2}\left(2ab+c^2\right)$ .

Les deux expressions sont égales, on a donc :

$\left(a+b\right)^2=2ab+c^2 \iff a^2+2ab+b^2=2ab+c^2 \iff a^2+b^2=c^2$