1. Activités pédagogiques
  2. Seconde
  3. Le théorème de Pythagore par Leonard de Vinci

Le théorème de Pythagore par Leonard de Vinci

Géométrie

Objectif

Courte activité géométrique pour la semaine des mathématiques !

On connaît plusieurs dizaines de démonstrations du théorème de Pythagore. On propose de s'intéresser à l'une de ces démonstrations, communément attribuée à Léonard de Vinci !

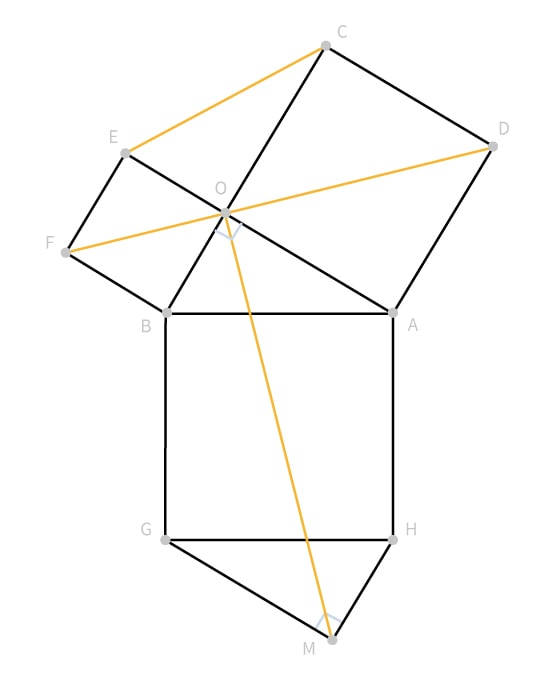
Figure géométrique.

Sur la figure ci-dessus, le triangle OAB est un triangle rectangle en O. Les quadrilatères OADC, BOEF et BAHG sont des carrés construits à partir des côtés de ce triangle rectangle.

On retrouve ici le début d'une démonstration bien connue, cependant Léonard de Vinci propose de construire un triangle MGH égal au triangle OAB, et donc rectangle en M.

  1. Il existe un autre triangle égal aux triangles OAB et GHM. Lequel est-il ? En déduire la relation entre les longueurs CE et BG.

    2. Le quadrilatère BOEF étant un carré, les côtés OB et EO sont de même longueur. De la même façon, les longueurs OA et OC sont de même longueur. De plus, l'angle OEC^\widehat{OEC} est un angle droit. On en déduit que les triangles OEC et OAB sont égaux.

    On a CE = BA = BG. Les longueurs CE et BG sont donc égales.

  2. Justifier que les aires des trapèzes DABF, OAHM, FECD et OBGM sont identiques.

    3. On peut démontrer les égalités :

    - des longueurs BF, HM, FE et OB ;

    - des longueurs AB, AH, EC et BG ;

    - des longueurs AD, OA, CD et GH ;

    - des angles FBA^,AHM^FEC^\widehat{FBA}, \widehat{AHM} \widehat{FEC} et GBO^;\widehat{GBO} ;

    - des angles BAD^,OAH^,ECD^\widehat{BAD}, \widehat{OAH}, \widehat{ECD} et MGB^.\widehat{MGB}.

    On pourra détailler les différentes symétries et transformations autour de ces trapèzes.

  3. En déduire que les hexagones ABFECD et OAHMGB ont des aires identiques.

    4. Les deux hexagones sont constitués des mêmes figures, c'est-à-dire de deux trapèzes, leurs aires sont donc identiques.

  4. En déduire que l'aire du carré BAHG est égal à la somme des aires de OBFE et OADC.

    5. On sait que les aires des deux hexagones ABFECD et OAHMGB sont identiques. Si l'on soustrait à chacune de ces aires l'aire des triangles qui la composent, c'est-à-dire OEC et OAB pour l'un, OAB et GHM pour l'autre, alors, étant donné que tous ces triangles sont égaux, les surfaces restantes restent égales. On a bien OA2+OB2=AC2OA^2+OB^2=AC^2.