Saison touristique
Pourcentages Taux d'évolution Indicateurs statistiques Outils de régression
Objectif
L'objectif de cette activité est de manipuler les pourcentages et les statistiques à travers l'exemple de la fréquentation hôtelière en Vendée, en séparant une série de données en deux (haute et basse saison) et en effectuant des comparaisons entre celles-ci. On pourra aussi aborder l'outil de régression linéaire en reliant la fréquentation à la température moyenne mensuelle.
On s'intéresse à la fréquentation des hôtels en Vendée durant l'année 2018. Le compte s'effectue en milliers de nuitées par mois :
| Janvier | Février | Mars | Avril | Mai | Juin |
|---|---|---|---|---|---|
| 51,91 | 58,83 | 71,50 | 128,19 | 152,79 | 166,58 |
| Juillet | Août | Septembre | Octobre | Novembre | Décembre |
| 220,45 | 274,63 | 157,22 | 121,52 | 76,57 | 60,24 |
Source: www.insee.fr
-
Quel est le mois le plus fréquenté ?
Le mois d'août est le mois le plus fréquenté.
-
-
Quelle est la moyenne de fréquentation sur l'année 2018 ?
-
Donner les indicateurs statistiques courants pour cette série statistique (médiane, quartiles, etc…)
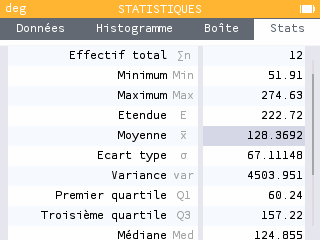
-
-
Exprimer, en pourcentage sur l'année, le nombre de mois pendant lesquels la fréquentation est inférieure à la moyenne.
Les mois d'octobre à avril connaissent une fréquentation inférieure à la moyenne. Cela représente 7 mois sur 12 soit 58% de l'année.
-
On appelle "basse saison" les mois pendant lesquels la fréquentation est inférieure à la moyenne.
Quelle est la fréquentation moyenne durant la "basse saison" ?
Quelle est la fréquentation moyenne durant la "haute saison" ?
Quel est le taux d'évolution de la fréquentation entre ces deux saisons ?
On pourra copier la colonne V1 en V2 en sélectionnant la cellule
V2 > Remplir avec une formule > Vide. Puis, après avoir appuyé sur la touche var, on cherche le sous-menuListespour retrouver les données entrées en V1.On pourra ensuite supprimer les cellules superflues dans les deux colonnes afin de ne conserver que les données relatives à la basse saison dans l'une, et celles relatives à la haute saison dans l'autre.
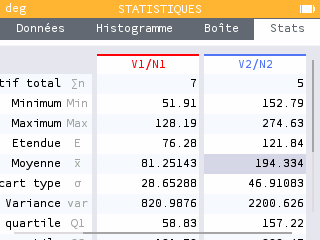
La moyenne de fréquentation en basse saison est de 81,25. La moyenne de fréquentation en haute saison est de 194,33. Cela représente un taux d'évolution égal à : soit 139%.
-
En janvier 2019, la fréquentation a augmenté de 16,4% par rapport au mois de janvier de l'année précédente. Quel était le nombre de nuitées en janvier 2019 ?
Il s'agit d'une augmentation de 16,4%. Le coefficient multiplicateur associé à cette évolution est donc de 1,164. La fréquentation en janvier 2019 était donc égale à :
On a recensé environ 60,42 milliers de nuitées en janvier 2019.
-
On s'interroge sur le lien de causalité qui pourrait exister entre la température moyenne et la fréquentation des hôtels. A l'aide du relevé des températures moyennes (en degrés) à la mi-journée en Vendée en 2018, proposer un hypothèse puis une méthode de vérification.
Janvier Février Mars Avril Mai Juin 11 7 11 16 19 23 Juillet Août Septembre Octobre Novembre Décembre 26 26 23 18 13 11 Source: www.historique-meteo.net
On propose de laisser les élèves utiliser l'application Régressions de la calculatrice.
On pourra réutiliser les données déjà entrées dans l'application Statistiques en sélectionnant la cellule
X1 > Remplir avec une formule > Vide. Puis, après avoir appuyé sur la touche var, on cherche le sous-menuListespour retrouver les données entrées en V1, N1, etc.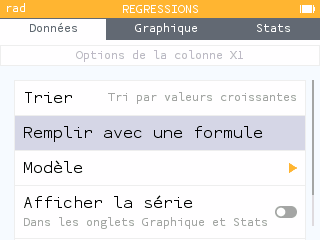
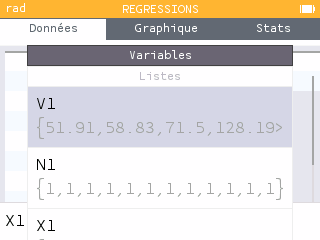
Après avoir entré les données dans la calculatrice, il suffit d'appuyer sur la touche OK pour choisir le modèle de régression. Le modèle linéaire est le plus connu des élèves. En explorant les différents modèles, ils pourront sans doute aussi se montrer convaincus par le modèle quadratique.
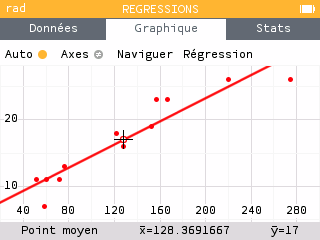
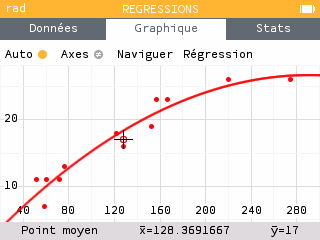
On appelle coefficient de détermination. On y accède en appuyant sur la touche OK une fois le modèle affiché. Compris entre 0 et 1, il donne un indication sur la fiabilité du modèle. Sa valeur est établie en utilisant l'écart entre les valeurs réelles et les valeurs établies par le modèle. Plus ce coefficient est proche de 1 et plus le pouvoir de prédiction est important.
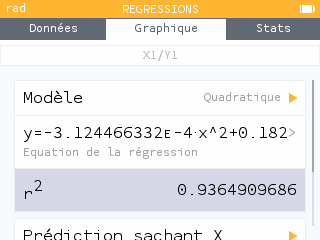
En comparant les , il semblerait que le modèle quadratique soit plus satisfaisant que le modèle linéaire. Cependant, les deux modèles ont leurs limites : on peut proposer aux élèves de "prédire" (toujours dans le menu accessible grâce à la courbe accessible via la touche OK) quelle serait la fréquentation si la température moyenne s'élevait à, par exemple, 40 degrés, selon chacun des deux modèles pour s'en convaincre !