Le PageRank de Google

Cette activité s’inscrit dans la thématique Le Web du programme de SNT. Elle est proposée par Christophe Mieszczak, actuellement professeur de mathématiques et d’ISN au lycée Léonard de Vinci à Calais.

• Contenu : Moteurs de recherche : principes et usages
• Capacités attendues : Mener une analyse critique des résultats fournis par un moteur de recherche.

Introduction

Le PageRank est l’algorithme d’analyse des liens hypertextes utilisé pour le classement des pages Web par le moteur de recherche Google. Le PageRank n’est qu’un indicateur parmi d’autres dans l’algorithme qui permet de classer les pages du Web dans les résultats de recherche. Ce système a été inventé par Larry Page, cofondateur de Google. Ce mot est une marque déposée.

Le principe de base est d’attribuer à chaque page une valeur proportionnelle au nombre de fois que passerait par cette page un utilisateur parcourant le Web en cliquant aléatoirement, sur un des liens apparaissant sur chaque page.

A chaque instant, des “robots”, appelés “spiders”, parcourent la toile, de lien en lien, et mettent ainsi sans cesse à jour le PageRank des pages du web.

Avec une pièce de monnaie

On schématise une page web par un cercle et les liens entre les pages par des flèches. Trois pages A, B et C sont donc représentées de la façon suivante.

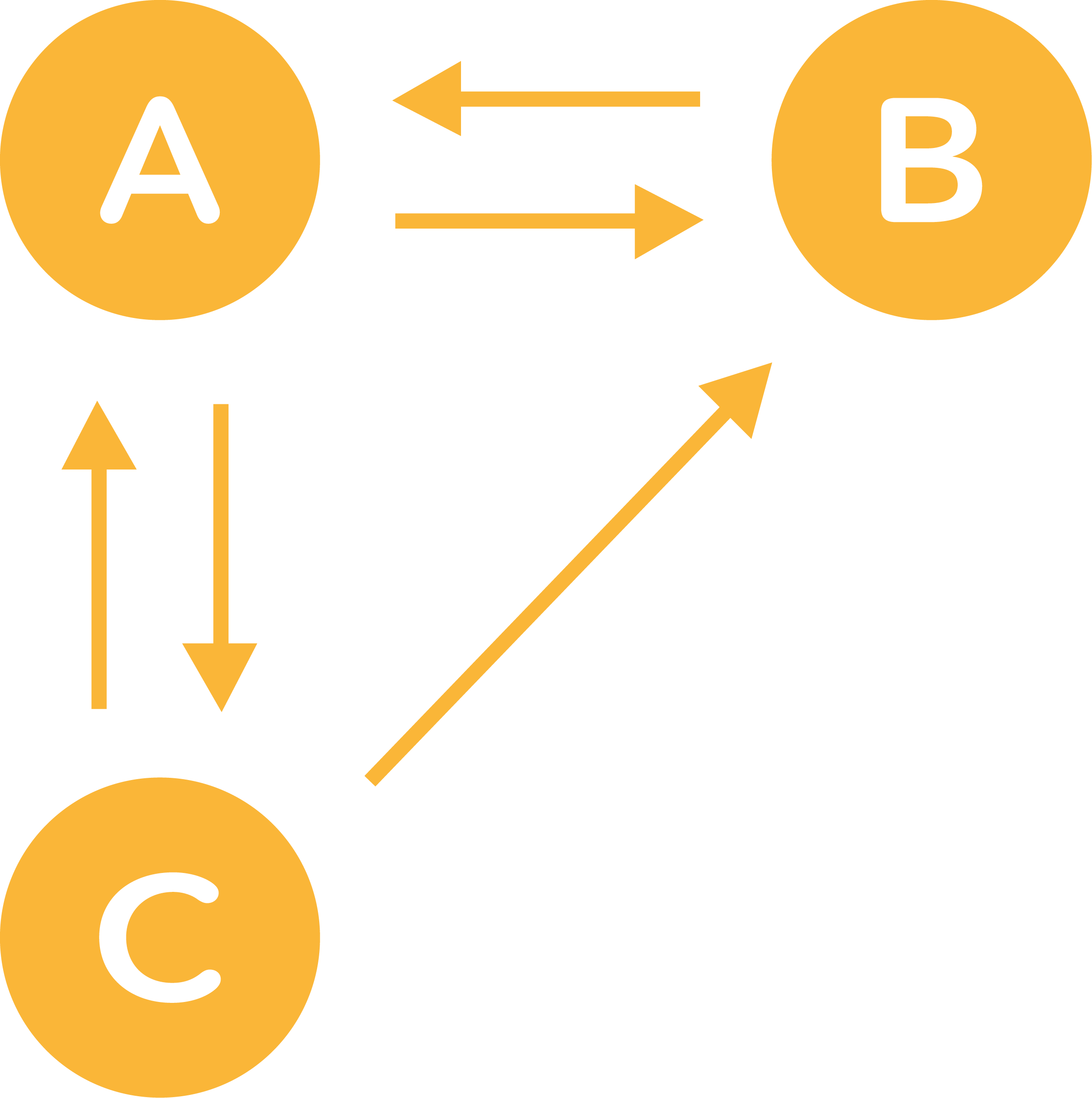
L’objectif est de déterminer la fréquence avec laquelle on visite chaque page lorsqu’on parcourt le graphe de façon aléatoire.

Au départ le nombre de visite de chaque page est nul.

On choisit une page de départ au hasard et on incrémente de 1 son nombre de visite (il passe donc à 1).

A l’aide d’une pièce de monaie équilibrée, nous allons nous promener sur ce graphe en respectant les règles ci-dessous:

• Si d’une page ne part qu’un seul lien alors on le suit.
• Si d’une page partent deux liens, on décide que l’un d’eux correspondra à face, l’autre à pile et on lance la pièce. Selon le résultat, on emprunte le lien correspondant.

A chaque nouvelle page atteinte, on augmente son nombre de visite(s) et on se déplace à nouveau.

Question 1

Réalisez cette expérience 30 fois puis donnez un PageRank à nos trois pages, c’est à dire leurs fréquences de visite.

On réalise l’expérience en partant de la page C. Voici la liste des résultats obtenus : C, A, B, A, B, A, C, B, A, B, A, B, A, C, A, B, A, C, B, A, B, A, C, B, A, C, A, C, A, B. On compte le nombre d’apparitions de A, B et C : $n_A=13$, $n_B=10$ et $n_C=7$.
Et donc les PageRank associés sont : $f_A=\frac{13}{30}=0.43$, $f_B=\frac{10}{30}=0.33$ et $f_C=\frac{7}{30}=0.23$.

Simulation Python

Question 2

Créez un nouveau programme Python et appelez le pagerank.py. Importez le module random qui sera nécessaire pour cette activité en tapant from random import * dans le script. Définissez ensuite une fonction nommée PR(n) dont l’objectif sera de réaliser n déplacements aléatoires sur le graphe précédent puis de renvoyer les résultats attendus.

On note nA, nB et nC les variables entières égales au nombre de visites des pages A, B et C.

Question 3

Commencez, dans notre fonction, par les définir en les initialisant à 0.

On définit les 3 variables.

La page en cours de visite sera modélisée par la variable page qui pourra prendre les valeurs "A" ou "B" ou "C". Pour démarrer il nous faut donc choisir au hasard entre A, B et C. Pour cela on va utiliser la fonction randint(a,b) du module random. Cette fonction génère un nombre aléatoire entre a et b.

Question 4

Définir la variable start=randint(0,2) qui choisit de façon équiprobable un nombre aléatoire entier dans {0,1,2} puis distinguer les cas suivants à l’aide d’un test “if” :

• Si start vaut 0 alors page sera égal à "A" et nA à 1.
• Sinon si start vaut 1 alors page sera égal à "B" et nB à 1.
• Sinon page sera égal à "C" et nC à 1.

On distingue les trois cas avec if, elif et else.

Il faut maintenant définir une boucle qui visitera n pages aléatoirement. A chaque “tour” de cette boucle :

• Si page est égal à "A" d’où partent deux liens, on définit alea=randint(0,1) :
  • si alea vaut 0 alors on passe à la page “B” et nB augmente de 1
  • sinon on passe à la page “C” et nC augmente de 1
• Sinon si page est égal à "B" d’où part un seul lien alors on passe à la page “A” et nA augmente de 1
• Sinon (on est forcément sur la page C d’où partent deux liens), on procède de la même façon que pour la page “A” afin de choisir entre A et B.

Question 5

Ecrire cette boucle.

Il faut faire bien attention à l’indentation dans la disjonction des cas et des sous-cas.

for i in range(n):
	if page=="A":
		alea=randint(0,1)
		if alea==0:
			page="B"
			nB=nB+1
		else:
			page="C"
			nC=nC+1
	elif page=="B":
		page="A"
		nA=nA+1
	else:
		alea=randint(0,1)
		if alea==0:
			page="A"
			nA=nA+1
		else:
			page="B"
			nB=nB+1

Une fois la boucle terminée, il faut renvoyer les résultats attendus, c’est-à-dire les fréquences de visite de “A”, “B” et “C” après n+1 parcours (en comptant le choix de départ).

Question 6

Définir ainsi les variables fA, fB et fC qui désignent les fréquences de visite des trois pages et terminer la fonction par return fA, fB, fC.

Les fréquences sont définies de la manière suivante :
$f=\frac{\text{nombre d'apparition de la page}}{\text{nombre d'expériences réalisées}}$

Question 7

Testez votre algorithme avec 100 puis 1000 puis 10000 déplacements. Classez A, B et C par popularité.

Rendez-vous dans la console Python en sélectionnant les trois points à gauche du nom du script et en choisissant Exécuter le script. Tapez ensuite PR(100), PR(1000) et PR(10000) et observez les résultats. On a ici ajouté les instructions round(fA,2), round(fB,2) et round(fC,2) dans le script pour arrondir les fréquences à deux chiffres après la virgule.

Les résultats de la question 1 étaient finalement assez proches de ce que l’on obtient ici !

Un premier cas particulier

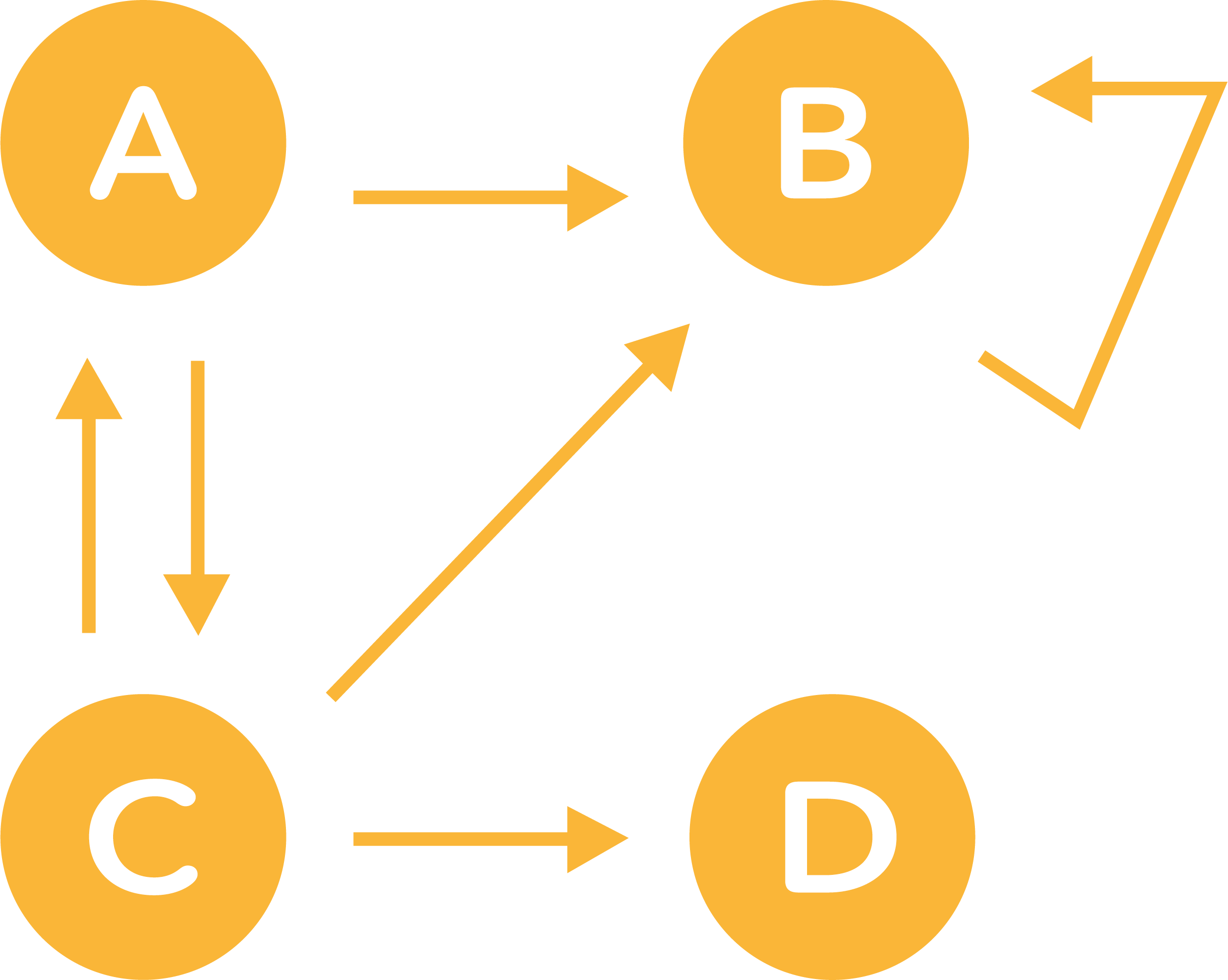
Voici un nouveau graphe qui contient cette fois quatre pages : A, B, C et D.

Question 7

Observez le nouveau graphe représentant les liens entre les pages A, B, C et D et identifiez quel est le problème.

Si l’on se retrouve sur la page B, il n’y a aucun moyen de revenir sur les pages A, C ou D. De même, la page D ne mène à aucune autre page.

Pour pallier à ce problème, on décide que si la page visitée ne redirige pas vers une autre page, alors on choisit au hasard la page suivante parmi les autres.

Question 8

Adapter la fonction PR(n) pour calculer le PageRank des pages A, B, C et D. Testez ensuite votre algorithme avec 100 puis 1000 puis 10000 déplacements. Classez A, B, C et D par popularité.

Voici les résultats obtenus après avoir modifié la fonction :

Un deuxième cas particulier

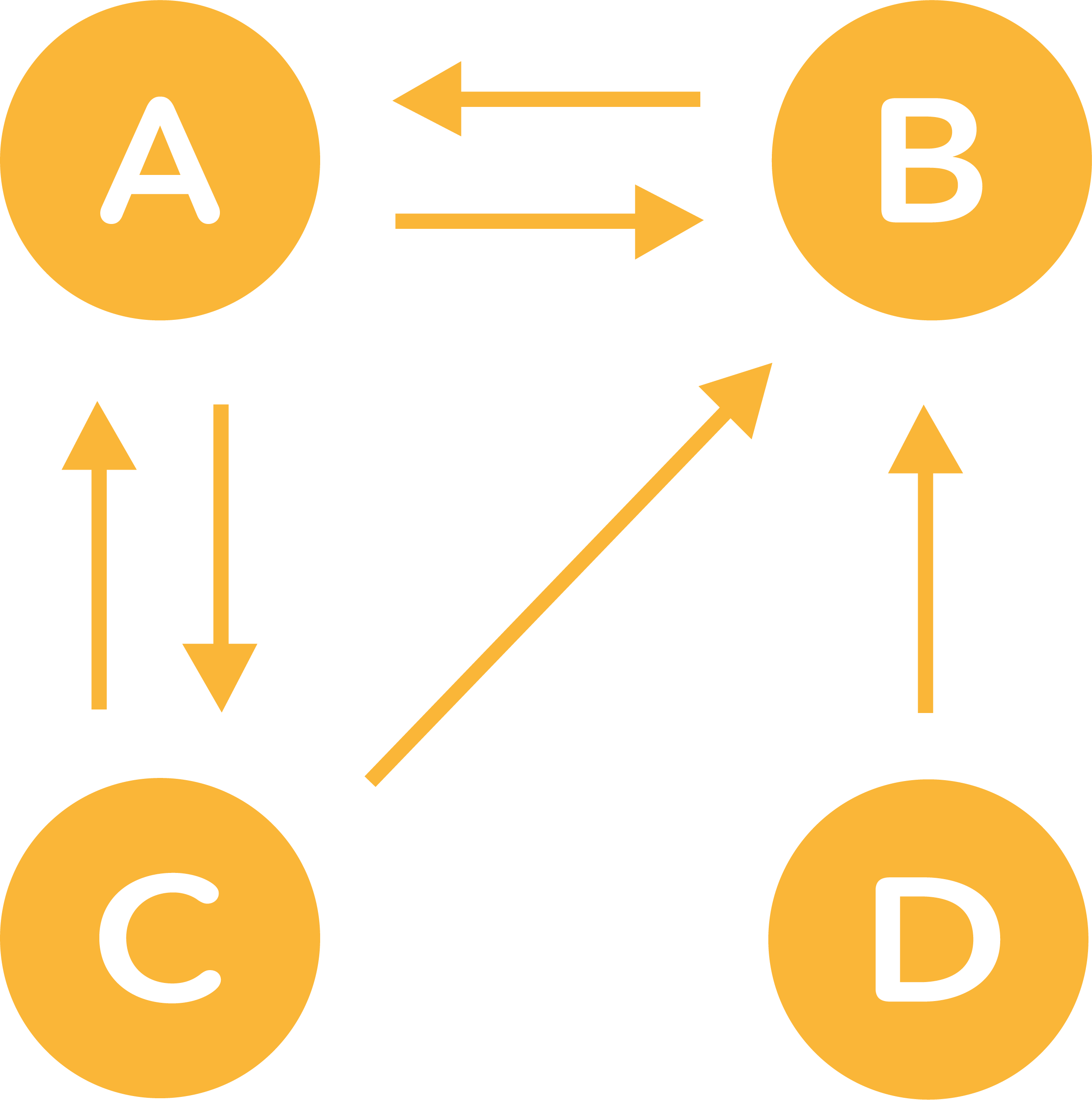
Voici un nouveau graphe.

Question 9

Observez le graphe et trouvez quel est le problème.

Aucune page ne mène vers la page D.

Pour pallier à ce problème on décide que, à chaque page visitée quelle qu’elle soit, on choisit une fois sur vingt la page suivante au hasard parmi toutes les pages.

Question 10

Adapter la fonction PR(n) pour calculer le PageRank des pages A, B, C et D. Testez ensuite votre algorithme avec 100 puis 1000 puis 10000 déplacements. Classez A, B, C et D par popularité.

Voici les résultats obtenus après avoir modifié la fonction :

On a ajouté une disjonction de cas en début de boucle pour tester si nA, nB, nC ou nD n’est pas multiple de 20 :

if nA%20==0 or nB%20==0 or nC%20==0 or nD%20==0:
	alea=randint(0,3)
	if alea==0:
		page="A"
		nA=nA+1
	elif alea==1:
		page="B"
		nB=nB+1
	elif alea==2:
		page="C"
		nC=nC+1
	else:
		page="D"
		nD=nD+1