Esta ficha foi redigida por Claire Savinas, professora da Escola Jean Vilar em Villeneuve-Lès-Avignon, França. A Claire é formadora em Python.

Objetivos da ficha

• descobrir o loop for
• utilizar uma função
• criar uma função com dois argumentos

Ficha de atividades para os alunos

Problema a resolver

No dia do nascimento do seu neto, a avó do João depositou na sua conta bancária bloqueada a quantia de 1 000 euros. Os juros, de 1,75 % ao ano, entram na conta todos os anos. No dia de aniversário da criação da conta, os juros são calculados a partir do montante na conta e depositados na mesma. Supondo que o João não fez nenhum novo depósito, qual o montante disponível na conta:

(a) no dia do seu primeiro aniversário

(b) no dia do seu segundo aniversário

(c) no dia em que fez 18 anos

Dica: Preencher uma tabela para calcular o montante disponível em cada ano.

Descobrir a utilidade do laço for

(a) Vamos começar por criar um novo script chamado atividade3.py.

Vamos inserir a função no script atividade3.py e de seguida selecionar a opção Executar o script no menu de três pontos à direita do nome. A função criada passa a estar disponível no menu da tecla var. Experimente usar diferentes valores nesta função, por exemplo conta(1), conta(2), conta(5), …

(b) Com a ajuda desta função, verifique as respostas para as questões anteriores.

Melhorar a função

(a) Modifique o guião anterior de modo a que este tome também como entrada a quantia que estava na conta quando o João nasceu.

(b) Usando esta função, calcule o montante que estará disponível na conta quando o João fizer 18 anos, se o depósito inicial for de 3 000 euros.

Correção da ficha

Problema para resolver

(a) $1 000 \times 1,0175 = 1 017,5$
No dia do seu primeiro aniversário, o João terá na sua conta 1 017,5 euros.

(b) $1 017,5 \times 1,0175 \approx 1 035,31$
No dia do seu segundo aniversário, o João terá na sua conta 1 035,31 euros.

(c) $1 000 \times 1,0175^{18} \approx 1 366,53$
No dia em que fizer 18 anos, o João terá na sua conta 1 366,53 euros.

Descobrir a utilidade do laço for for

(a) Escrevendo conta(1) obtém-se 1 017,5.

Escrevendo conta(2) obtém-se 1 035,31.

Escrevendo conta(18) obtém-se 1 366,53.

(b) Para verificar as respostas obtidas na função anterior, utilizamos na função os valores 1, 2 e 18 : conta(1), conta(2) e conta(18).

Melhorar a função

(a)

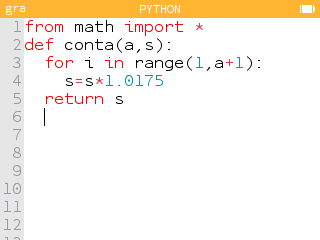
(b) Adicionando conta(18,3000), obtemos 4 099,59 euros.