Road Trip
Average rate of change Instantaneous rate of change
Objective
The objective of this activity is to explore how to calculate average rates of change in the context of a road trip. Students create graphs given specific scenarios and estimate the average speed between two points. This activity also leads into a discussion about how average rate of change compares to the instantaneous rate of change.
A road trip to Charlotte
Rashmi is taking a trip from Durham, NC to Charlotte, NC this weekend. It takes Rashmi 3 hours to drive the 150 mile trip. What is Rashmi's average speed for her trip?
To determine Rashmi's average speed, we can calculate the change in distance over the change in time.

Rashmi's average speed is 50 miles per hour.
Choose your own adventure
Choose one of the scenarios below. Sketch a possible graph that would represent Rashmi's Distance from Durham over Time for that scenario. Then describe the rate of change throughout Rashmi's trip in your chosen scenario.
- Rashmi sets her car's cruise control to 50mph for the entire trip.
- Rashmi's foot pushes steadily further down on the accelerator as she gets closer to Charlotte.
- Rashmi gets tired and lets up on the pedal throughout the trip.
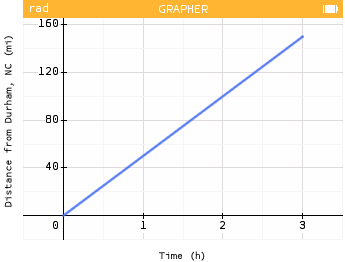
The rate of change is constant throughout the trip.
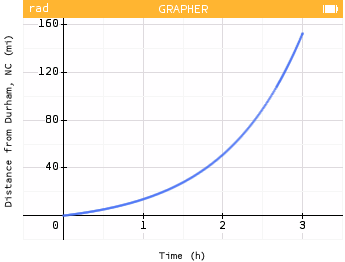
The rate of change is increasing throughout the trip.
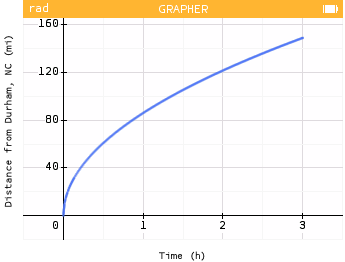
The rate of change is decreasing throughout the trip.
A graphical representation
The figure below shows the graph of the function f(t) which represents Rashmi's distance from Durham as a function of elapsed time t.
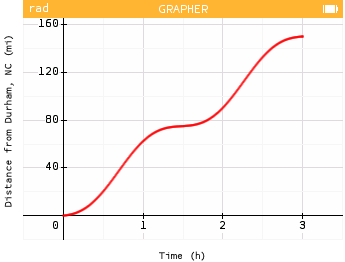
Think about what is happening during Rashmi's trip. Pick 2 or 3 key features of the graph and explain what they might mean in context.
Answers may vary. Students may notice that the graph is not completely linear, illustrating that Rashmi's speed is changing during the trip. Students may notice that there are times where Rashmi is traveling less distance over a certain time period compared to others which means she is driving at a lower speed.
Calculate an average rate
Two points on Rashmi's trip have been marked, A(1, 62) and B(2, 90), as shown below.
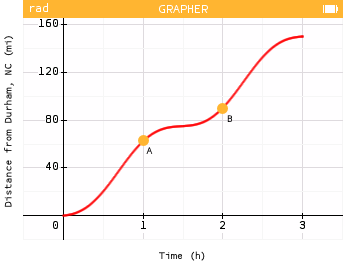
- What do the values of these coordinates represent?
- Describe how you could use these points to approximate Rashmi's average speed between hour 1 and hour 2 of her trip? Use your method to determine her average speed between these times.
Point A represents Rashmi's location after 1 hour. She has driven 62 miles from Durham. Point B represents Rashmi's location after 2 hours. She has driven 90 miles from Durham.
We can approximate Rashmi's average speed between hour 1 and hour 2 by computing the change in distance over the change in time for this interval.

Rashmi's average rate of change was 28 miles per hour.
How fast was she going?
Rashmi wants to know how fast she was going at exactly the 2 hour mark. Do you think her average speed from the previous question is an overestimate or an underestimate of her speed at the 2 hour mark? Explain your answer.
The average speed between the first and second hour mark found in the previous answer is an underestimate of the exact speed at hour 2. Between the two hour marks, Rashmi's rate of change is almost zero as indicated by the flatness of the curve. This will bring the average rate of change down compared to the her speed at hour mark 2.