Terminal
Riemann Sum Accumulation Average Rate of Change Instantaneous Rate of Change
Objective
The objective of this activity is to interpret the meaning of derivatives and integrals in the context of the tasks performed by an airline crew.
Have you ever been to an airport and flown on an airplane? If so, you have probably seen a lot of planes landing and taking off. Have you ever watched all the activity that takes place once the plane reaches the terminal? A lot more than just unloading and loading passengers goes on during the time between landing and take off!

Fill 'er up!
Jet fuel is pumped into a plane at a rate modeled by liters per minute for , where t is measured in minutes.
- How many liters of fuel are pumped into the plane during the first 5 minutes?
- Determine . Using correct units, explain the meaning of in the context of the problem.
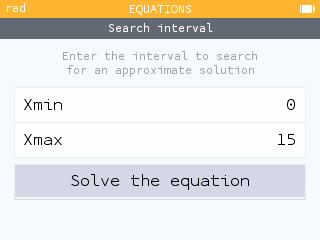
- How long does it take to pump 10,000 liters of fuel?
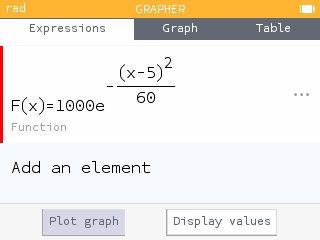
Using the Grapher app, enter . Because is the rate function, the area under represents the change in fuel. That is, the area represents the amount of fuel pumped into the plane. On the Graph tab, we can calculate the integral.
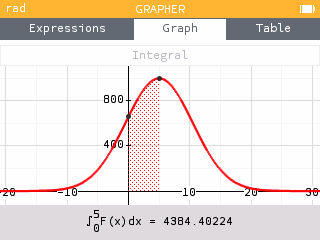
4,384.4 liters of fuel are pumped into the plane during the first 5 minutes.
The derivative of at can be found by turning on the derivative values within the Options of the function.
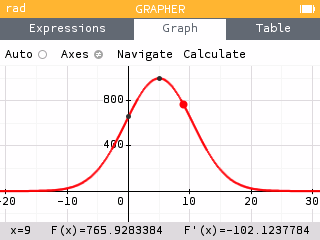
We see that . The rate that fuel is being pumped into the plane is decreasing by 102.124 l/min per minute at time .
To determine how long it will take to pump 10,000 liters, we need to solve the equation
where . This equation can be solved using the Equations app.

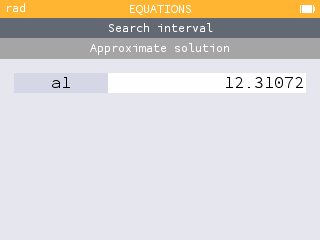
It will take 12.311 minutes to pump 10,000 liters of fuel.
H2O on the Go!
Potable water is used in the sinks and toilets of the bathroom and sometimes for making tea and coffee. A water truck pumps potable water into a plane's water tanks at a rate modeled by liters per minute for , where t is measured in minutes. At the same time, waste water is removed from the plane at a rate modeled by liters per minute, where is differentiable and decreasing on 0 ≤ t ≤ 10. Selected values of W(t) are shown in the table below. At , there are 250 liters of combined water (potable and waste) on the plane.
| t (minutes) | 0 | 2 | 4 | 7 | 10 |
|---|---|---|---|---|---|
| (liters/min) | 27 | 23 | 17 | 9 | 5 |
- Estimate . Show the work that leads to your answer. Indicate units of measure.
- Use a left Riemann sum with the four subintervals indicated by the table to estimate the total amount of waste water removed from the plane during the 10 minutes. Is this an overestimate or an underestimate of the total amount of water removed? Give a reason for your answer.
- Estimate the total amount of combined water (potable and waste) in the plane after 10 minutes.
We can estimate by evaluating the average rate of change over the interval to .

liters/min2.
liters
A left Riemann sum will be an overestimate since is a decreasing function.
Total combined water

Total combined water
There are 176.167 liters of combined water on the plane after 10 minutes.
Cargo, Cargo, Cargo!
Airlines require you to check your larger bags. Checked bags are stored in the bottom of the plane. When a plane arrives at its terminal, the luggage for passengers arriving has to be removed and the luggage for passengers departing has to be stored. The number of bags on the plane during this process can be modeled by bags, for , where t is measured in minutes.
- At what time , , is the number of bags on the plane at a minimum? Justify your answer.
- Find the average rate of change for over the interval 0 to 20. Indicate units of measure.
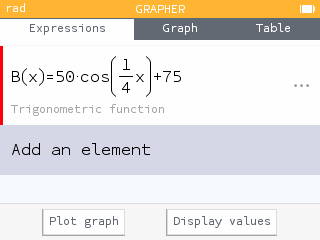
Using the Grapher app, enter the function .
Before viewing the Graph, adjust the Plot restriction in the options to match the practical domain for this scenario.
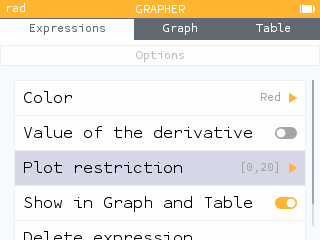
Graphing the function, we see the minimum occurs at .
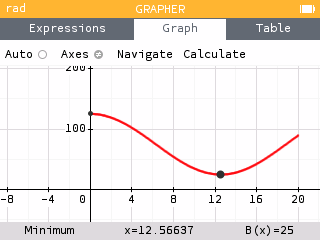
That is, the number of bags on the plane is at a minimum of 25 bags at time minutes.
The average rate of change for B(t) over the interval 0 to 20 can be determined by evaluating

The average rate of change for B(t) is -1.791 bags per minute.