Acetaminophen
Recursive Functions Half-life Equilibrium Modeling
Objective
The objective of this activity is to use algebraic representations to build recursive equations that represent the levels of acetaminophen in the body.
Headaches are common concerns for many individuals. There are numerous over-the-counter medications that are available to relieve headaches, including acetaminophen.
It is theorized that acetaminophen blocks an enzyme that sends out chemicals that make our bodies feel pain. Once entering your body, like many other medications, acetaminophen is processed in the liver into harmless substances and removed from your body.
Half-Life
The half-life of acetaminophen in healthy young adults is approximately 2.5 hours. This means that it takes about 2.5 hours for the concentrations of acetaminophen to decrease by 50%.
- What percent of acetaminophen is removed from the body after 4 hours?
- What percent of acetaminophen is removed from the body after 6 hours?
- How long will it take for 99% of the acetaminophen to be removed from the body?
To determine the percent of a substance with a half-life of hours remaining after hours, we use the formula .
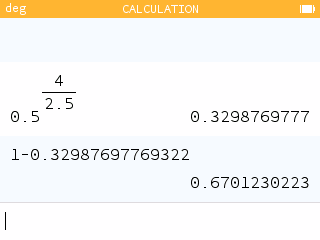
67% of acetaminophen is removed from the body after 4 hours.
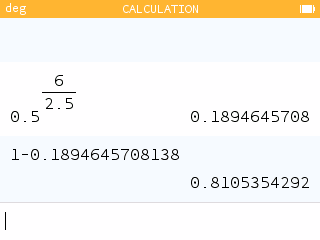
81% of acetaminophen is removed from the body after 6 hours.
If 99% of the acetaminophen is removed, only 1% remains. To find the time , use the Equations app to solve .


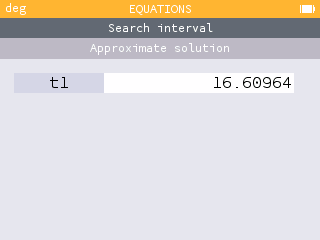
It will take 16.6 hours for 99% of acetaminophen to be removed from the body.
Regular and Extra Strength
For a common brand of acetaminophen, one "Regular Strength" capsule contains 100mg of acetaminophen and the "Extra Strength" capsules each contain 500mg of acetaminophen.
- To relieve her headache, Ranya decides to take two "Regular Strength" capsules. Write a set of recursive equations that represent the amount of acetaminophen in Ranya's body at the end of each four-hour period.
- How much acetaminophen will remain in her system 24 hours after taking the 200mg dose?
- Ehab prefers to take two "Extra Strength" capsules. Write a set of recursive equations that represent the amount of acetaminophen in Ehab's body at the end of each four-hour period.
- How much acetaminophen will remain in his system 24 hours after taking the 1000mg dose?

where n is measured in 4-hour periods.
To determine the amount of acetaminophen in her body after 24 hours, we look at .
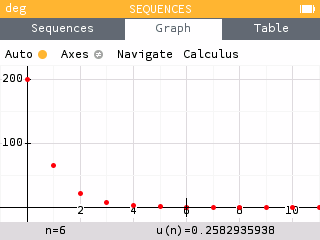
Since , she will only have 0.258 mg of acetaminophen left in her body.

where n is measured in 4-hour periods.
To determine the amount of acetaminophen in his body after 24 hours, we look at .
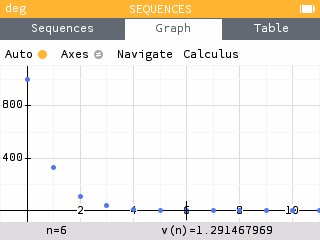
Since , he will only have 1.291 mg of acetaminophen left in his body.
Therapeutic Level
The therapeutic level of a drug in the bloodstream is the range within which that drug is expected to be effective. Acetaminophen has a therapeutic level of 10-20g/mL.
- The adult human body has appoximately 5L of blood. Determine the amount of acetaminophen needed in the body to feel the effects.
- Approximately how long will Ranya's "Regular Strength" medication be effective? How much longer will Ehab's "Extra Strength" medication be effective?
To determine the amount of acetaminophen needed, we multiply the amount of blood in the body by the lower and upper values of the therapeutic level range.

The acetaminophen is effective when 50-100mg are in the body.
Once the amount of acetaminophen drops below 50mg, the medication is no longer effective. For Ranya's "Regular Strength" medication, this occurs between n = 2 and n = 3. Therefore the medication is no longer effective sometime between 8 and 12 hours. Ehab's "Extra Strength" medication drops below 50mg between n = 3 and n = 4. Therefore his medication is effective for approxmiately 4 hours longer than Ranya's.
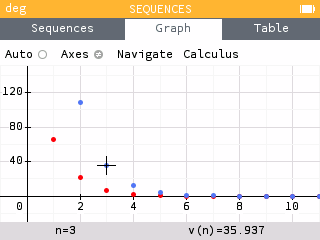
Continued Use
Both medications recommend taking two capsules every 6 hours.
- If Ranya takes an additional 200mg every six hours after her initial dose, write a set of recursive equations that represent the amount of acetaminophen in her body at the end of each six-hour period.
- How much acetaminophen will remain in her system 24 hours after taking the initial 200mg dose? 48 hours? 72 hours?
- If Ehab takes an additional 1000mg every six hours after his initial dose, write a set of recursive equations that represent the amount of acetaminophen in his body at the end of each six-hour period.
- How much acetaminophen will remain in his system 24 hours after taking the initial 1000mg dose? 48 hours? 72 hours?

where n is measured in 6-hour periods.
To determine the amount of acetaminophen in her body after 24 hours, we look at .
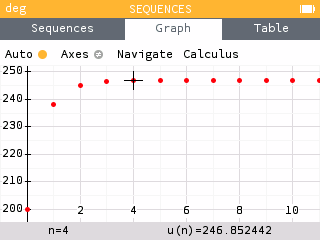
Since , she will only have 246.85 mg of acetaminophen left in her body.
Similarly, to determine the amount of acetaminophen in her body after 48 and 72 hours, we look at and
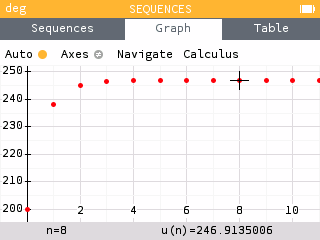
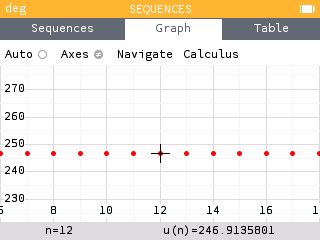
We see that we have reached an equilibrium value of approximately 246.91 mg.

where n is measured in 6-hour periods.
To determine the amount of acetaminophen in his body after 24 hours, we look at .
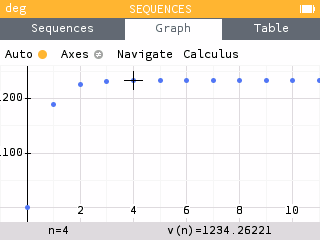
Since , he will only have 1234.26 mg of acetaminophen left in his body.
Similarly, to determine the amount of acetaminophen in his body after 48 and 72 hours, we look at and
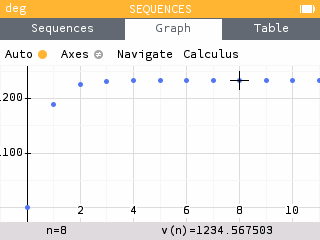
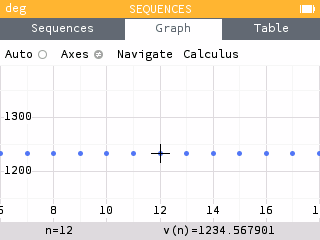
We see that we have reached an equilibrium value of approximately 1234.57 mg.
For more information on acetaminophen safety: