Daylight

Create a function

Below is a table containing the number of minutes of daylight on the 1st and 15th of each month in Paris, France during 2021.

1. Make a scatterplot of the relationship between the day of the year and the amount of daylight.



2. Describe what the scatterplot reveals about the relationship between the day of the year and the amount of daylight.

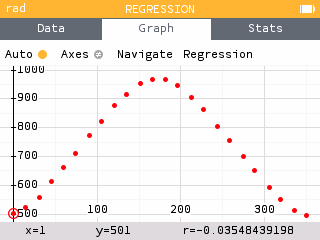
As the day of the year increases, the amount of daylight also increases at first, but then decreases. This corresponds to how there is more daylight in the summer (the middle of the year) but less during the winter.

3. Based on the scatterplot, what type of function do you think would best model the data?

A trigonometric function would best model the data.

4. Plot a regression model on your scatterplot. What is its equation?

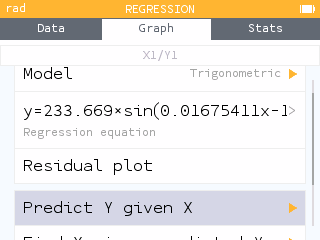
Using the Regression menu, we can add a trigonometric model.





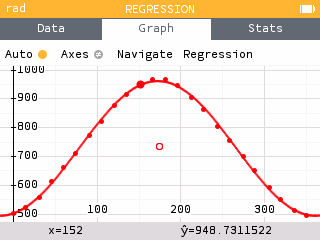
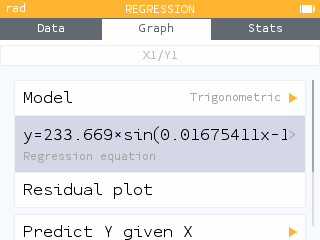
The equation of the model is $f\left(x\right)=233.669\sin\left(0.0168x-1.315\right)+728.3703$.

Analyze the function

In the previous section, you may have selected a sinusoidal function to model your data. If you chose another type of function, go back and apply a trigonometric regression and compare the models.

Use a trigonometric regression model to answer the following questions. To connect dates with their corresponding day of the year, here is a helpful resource.

1. Identify the amplitude of the regression model. Interpret its value in context.

The amplitude is $a=233.669$. This represents the difference between the maximum or minimum and the midline. Doubling this value tells us the difference in the maximum and minimum minutes of daylight throughout 2021. That is, the longest day has about 467 more minutes of daylight than the shortest day. That's almost 8 hours!

2. Identify the period of the regression model. Explain what it means in the context of this problem.

The period is $p = \frac{2\pi}{0.0168}=374$.



This should represent the number of days in one year. However, we know the real period is approximately 365 days.

3. Determine the maximum value of the function. Explain what this means in the context of the problem.

The maximum value can be found in two ways:

Option 1: Using the equation

The maximum can be found by adding the amplitude to the midline.

$233.669 + 728.3703$

$= 962.039$

Option 2: Using the graph

The maximum value can be found using the Maximum tool within the Calculate menu of the Grapher application.







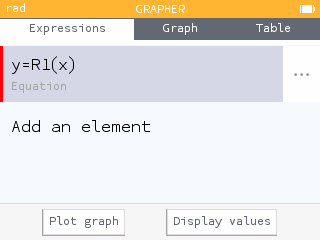
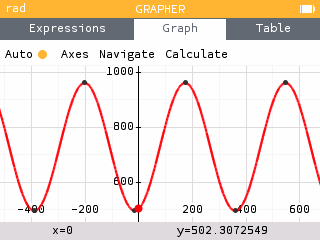
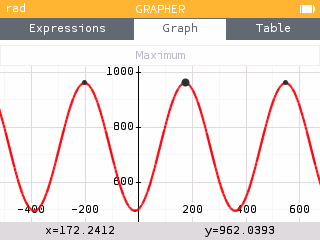
The maximum value is $y=962.039$ and occurs at $x=172.2$.

In context, this means that the 172nd day of the year (June 21) has the most daylight of around 962 minutes, or 16 hours!

4. September 10, 2021 (Day 253) is not a data point in the table. Use the regression model to predict the amount of daylight on this day.

The predicted amount of daylight can be found using the Predict Y given X tool within the Regression menu of the Regression application.







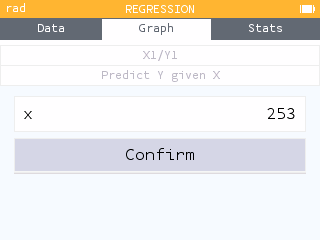
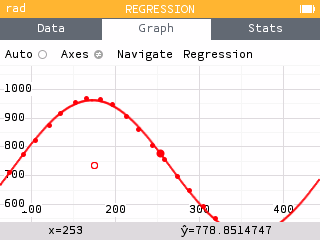
The predicted number of minutes of daylight on the 253rd day is 778.85 minutes, or approximately 13 hours of daylight.

5. On which date(s) in 2021 is it predicted that there will be 700 minutes of daylight?

The first day on which it is predicted to have 700 minutes of daylight can be found using the Find X given predicted Y tool within the Regression menu of the Regression application.







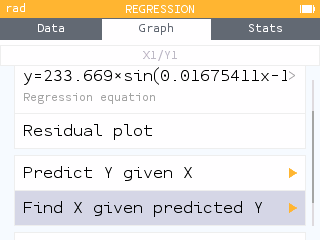
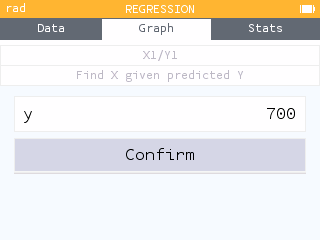
The first day of the year on which it is predicted to have 700 minutes of daylight is March 12.

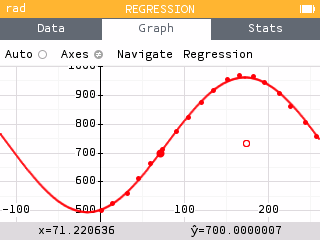
Because the Regression application only outputs the first positive x-value for a predicted y-value, it may be more useful to use the X given Y tool within the Calculate menu of the Grapher application.







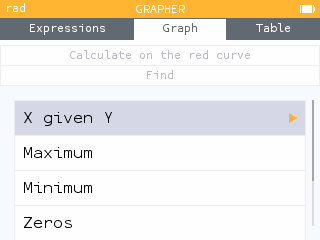
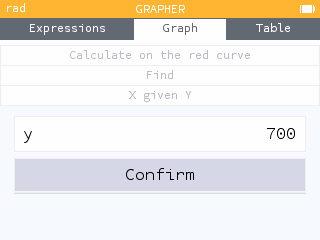
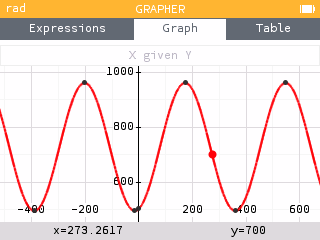
The two days within the year 2021 that are predicted to have 700 minutes of daylight are day 71 and day 273. That is, March 12 and Septemeber 30.

Extension

Navigate to www.timeanddate.com/sun. Search for a different city around the world and view its "Sunrise and Sunset" times. Scroll down on the page to see the amount of daylight each day in a given month.

The amount of daylight will be given in hours, minutes, and seconds. You can convert to minutes using the NumWorks calculator.

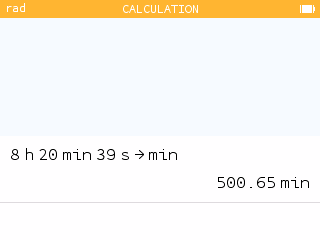
Record the number of minutes of daylight on the 1st and 15th of each month for 2021.

1. Create a scatterplot for your data and apply a trigonometric regression. What is the equation of your model?
2. Determine the amplitude and period.
3. Determine the minimum value of the function. Explain what this means in the context of the problem.
4. Use your model to predict the amount of daylight for September 10, 2021 (Day 253).
5. On which date(s) in 2021 is it predicted that there will be 700 minutes of daylight?
6. How do the values found above compare to those found from Paris, France? Why might these values be different?