During the 2021 Summer Olympics in Tokyo, competition climbing became an Olympic sport for the first time ever. Athletes competed in three separate disciplines: speed climbing, bouldering, and lead climbing. There were 20 men and 20 women who competed in the 2021 Olympic Sports Climbing Qualification Rounds.

In speed climbing, two climbers race side-by-side to scale identical routes on a 15m high wall set at an angle of 95 degrees.

The walls used for bouldering present a range of challenges, with overhangs and some holds so small that they can only be held by the fingertips. Climbers must plan each move carefully while constantly being aware of the 4 minute time limit. The goal is to complete as many routes as possible.

When lead climbing, athletes wearing harnesses attached to a climbing rope attempt to climb as high as they can on a taller wall measuring 15-20 meter within six minutes. The wall features 40-60 handholds. Climbers are scored on how far they progress, with each handhold earning 1 point.

Displaying Data with Graphs

The table below shows the number of holds attained by the 20 women during the Lead Climbing Qualification Rounds.

Source: Olympics.com

1. Determine the 5-number summary statistics for the data.

The 5-number summary statistics can be computed using the Statistics application. Input the number of holds attained in V1.





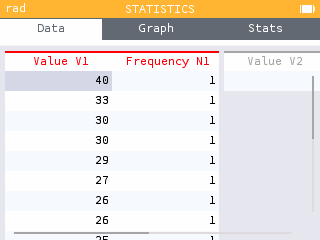
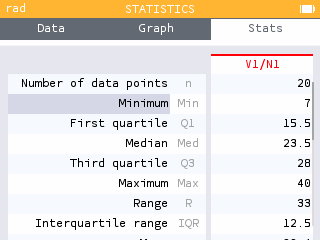
Use the Stats tab to obtain the necessary values

Min	Q1	Med	Q3	Max
7	15.5	23.5	28	40

2. Construct two different graphs of the data.

Use the Graph tab to construct a Histogram and Boxplot of the data.




3. Describe the distribution of the data in context, citing plots and the numerical summary statistics.

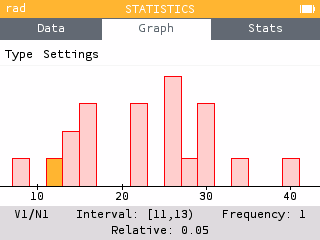
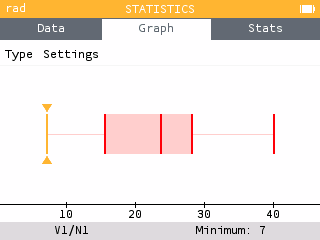
The distribution of holds attained by female Olympic climbers is fairly symmetric with one peak. The distribution is centered around the median of 23.5 holds with a range of 40-28 = 12 holds. There are no obvious outliers.

4. What are the advantages of each data display?

The boxplot provides a quick summary of the distribution but the histogram shows the shape of the distribution.

Identifying Outliers

The table below shows the number of holds attained by the 20 men during the Lead Climbing Qualification Round.

Source: Olympics.com

1. Construct a boxplot of the data.

A boxplot can be constructed using the Statistics application. Input the number of holds attained in V1. Select the boxplot from the Graph tab.



2. French athlete, Bassa Mawem, was injured on the seventh hold. Mathematically show that Mawem's value is considered an outlier.

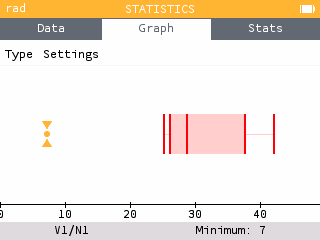
The data point 7 is an outlier if it falls below Q1 - 1.5(IQR). For this dataset, Q1 = 26 and IQR = 11.5. Therefore, the cutoff value is 26 - 1.5(11.5) = 8.75. Since 7 < 8.75, Mawem's value is an outlier.

3. Which measure of center and spread best describes the distribution of the number of holds attained by Olympic male climbers?

The mean and standard deviation are not resistant to outliers. Therefore, the median and IQR should be used to describe the distribution.

Comparing Distributions

The table below shows the times (in seconds) of the 20 men and 20 women during the Speed Climbing Qualification Round.

Source: Olympics.com

1. Construct an appropriate graph to compare the times of the two genders.

Use the Histogram or Box options from the Graph tab to construct graphs to compare the data.




2. Compare the distribution of the data in context.

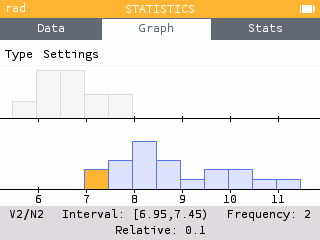
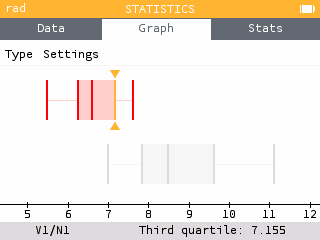
Answers may vary. The average climbing time was less for men than women (around 6.5 seconds for men compared to around 8.5 seconds for women). The climbing time for women varied more than it did for men as both the standard deviation and IQR were 2-3 times larger for women than men. The distribution of for women's climbing time appears to be slightly skewed right whereas the distribution for men may be slightly skewed left. Neither distribution of climbing times appears to have outliers.

---

For more information on Olympic Sport Climbing:

• Olympics Website