Démographie de l'Afrique du Sud
Outils de régression Taux de variation
Objectif
L'objectif de cette activité est d'utiliser les données démographiques de l'Afrique du Sud afin de réaliser quelques prédictions à l'aide des régressions ainsi que des calculs sur les taux d'évolution.
Savoir-faire
-
Produire et interpréter des graphiques statistiques traduisant l'évolution d'effectif d'une population ou de ressources, notamment sous forme de nuages de points. À l'aide d'une calculatrice ou d'un tableur, ajuster un nuage de points par une droite et utiliser ce modèle linéaire pour effectuer des prévisions.
-
À partir de données démographiques, calculer le taux de variation d'une population entre deux dates.
-
À l'aide d'un tableur, d'une calculatrice ou d'une représentation graphique, calculer le temps de doublement d'une population sous l'hypothèse de croissance exponentielle.
-
Comparer les valeurs fournies par un modèle à des données réelles afin de tester sa validité.
On s'intéresse aux données relatives au nombre d'habitants (en millions) en Afrique du Sud entre 1960 et 1995.
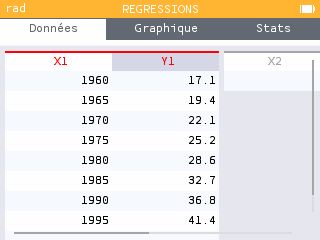
| Année | 1960 | 1965 | 1970 | 1975 | 1980 | 1985 | 1990 | 1995 |
|---|---|---|---|---|---|---|---|---|
| Population | 17,1 | 19,4 | 22,1 | 25,2 | 28,6 | 32,7 | 36,8 | 41,4 |
Source : La Banque mondiale
Nous allons utiliser l'application Régressions afin de mettre en évidence un modèle fiable capable de décrire l'évolution de la population entre 1960 et 1995, ce qui nous permettra par la suite de réaliser des prévisions.
-
On s'intéresse tout d'abord au taux de variation de la population.
-
Calculer le taux de variation entre 1960 et 1965 puis entre 1990 et 1995. On donnera le résultat sous la forme d'un pourcentage arrondi à 10-1 près.
-
On considère que le taux de variation est relativement stable entre 1960 et 1995 et que la population augmente en moyenne de 13,5% tous les cinq ans. Quel est donc le taux de variation annuel ?
On pourra utiliser la racine n-ième qui se trouve dans la boîte à outils Toolbox.
On calcule un taux de variation égal à 13,4% entre 1960 et 1965, et égal à 12,6% entre 1990 et 1995.
On sait que tous les cinq ans, la population est multipliée par 1,135. Par conséquent, le taux de variation annuel est égal à .
Chaque année, la population croit en moyenne d'environ 2,6%.
-
-
Entrer les données du tableau précédent dans l'application Régressions. On entrera en Y1 les données relatives à la population en millions de personnes.
-
On a vu que le taux de variation restait relativement stable entre 1960 et 1995. Quel modèle semble donc le plus approprié pour décrire nos données ? On pourra vérifier en testant les différentes régressions à l'aide de la touche OK ou le menu Régression dans l'onglet Graphique.
-
Toujours à l'aide du menu "Régression" de l'onglet Graphique, il est possible d'avoir accès à des prévisions, c'est-à-dire des lectures de courbe en fonction de l'une ou l'autre de nos variables.

En 1960, la population en Afrique du Sud était environ de 17 millions. D'après le modèle exponentiel, en quelle année la population a-t-elle doublé ? On donnera si possible le mois durant lequel cela s'est produit.
-
D'après le modèle exponentiel, quelle sera la population en 2020 ? Et en 2050 ? On arrondira les résultats au million.
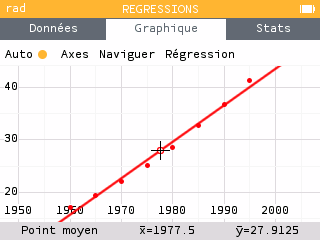
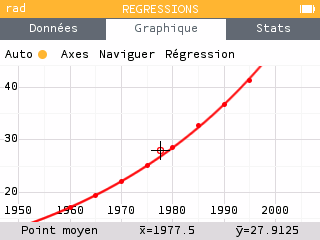
Lorsque le taux de variation semble constant, c'est le modèle exponentiel qui est le plus approprié. On peut le vérifier en comparant les deux modèles de régression : avec une régression linéaire, les points ne semblent pas alignés avec le modèle. Avec un modèle exponentiel, les points semblent tous se trouver sur la courbe.
On réalise une prédiction connaissant la valeur de Y avec . C'est à la fin de l'année 1986 que la population a doublé, d'après notre modèle.
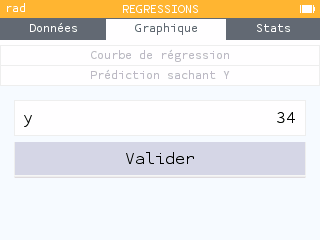
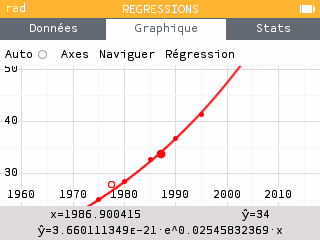
Pour connaître plus précisément le moment de l'année où cela s'est produit, il faut répartir 0,926335 sur une année, soit 12 mois ou 365 jours. Cela correspond au 338e jour de l'année, soit au mois de décembre !
On réalise maintenant une prédiction sachant X.
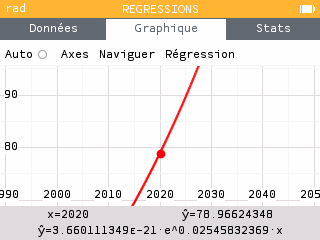
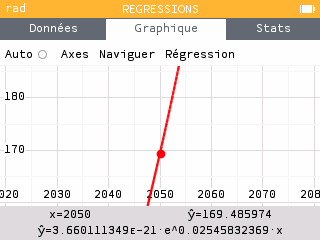
La population sera donc égale à 79 millions en 2020 et 169 millions en 2050 d'après ce modèle.
-
-
En 2020, on comptait 59 308 690 habitants en Afrique du Sud. Que penser de notre modèle ?
-
On propose à nouveau d'entrer les données dans l'application Régressions, dans un deuxième tableau. On pourra masquer le premier en sélectionnant la cellule X1, touche ok, et décocher la case
Afficher la série.-
Quel modèle de régression semble le plus approprié pour ces données ? On donnera l'équation correspondant à ce modèle avec des coefficients arrondis à 10-2 près.
-
D'après l'équation obtenue, de combien d'habitants la population augmente-t-elle en moyenne chaque année ?
-
Quelle prédiction peut-on faire pour l'année 2050 avec ce modèle ? On proposera une lecture graphique ou un calcul pour répondre à cette question, en arrondissant au million.
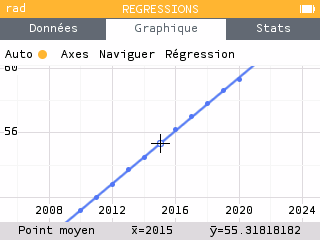
Dans ce cas-ci, c'est la régression linéaire qui semble appropriée. On obtient une relation entre X et Y telle que : .
Le coefficient directeur de la droite est égal à 0,82 ce qui signifie que pour chaque unité, la droite augmente de 0,82. Dans notre contexte, chaque année, la population augmente de 0,82 million soit 820 000 habitants.
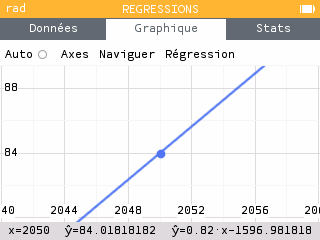
La calculatrice nous prédit 84 millions d'habitants pour 2050.
Par le calcul, on obtient une valeur semblable en remplaçant x par 2050 dans l'équation précédente : soit 84 millions d'habitants.
-
Notre modèle n'est plus valable puisqu'il surestime largement la population en Afrique du Sud en 2020.
Afin d'améliorer notre modèle et nos prévisions, on dispose de données plus récentes, relatives à la population de l'Afrique du Sud (en millions) entre 2010 et 2020 :
| Année | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Population | 51,2 | 52,0 | 52,8 | 53,7 | 54,5 | 55,4 | 56,2 | 57,0 | 57,8 | 58,6 | 59,3 |
Source : La Banque mondiale