Modèles démographiques
Suites numériques
Objectif
Cette activité vise à introduire les suites numériques et l'utilisation de la calculatrice dans leur manipulation à travers les prédictions de Malthus.
Savoir-faire
-
Exprimer u(n) en fonction de u(0) et n. Produire et interpréter des graphiques statistiques traduisant l'évolution d'effectif d'une population ou de ressources, notamment sous forme de nuages de points.
-
À partir de documents fournis, proposer un modèle de croissance de ressources alimentaires (par exemple la production mondiale de blé ou de riz) et la comparer à une croissance exponentielle.
Thomas Malthus est un économiste britannique ayant vécu peu avant la révolution industrielle. S'intéressant aux évolutions conjointes des moyens de production et de la population anglaise, il publie en 1798 un ouvrage dans lequel il prédit une véritable catastrophe démographique : si la population continue de croître exponentiellement, les ressources, qui croissent de façon linéaire, finiront par manquer. Il prône alors le contrôle des naissances et d'autres mesures extrêmes, afin d'éviter cette insuffisance.
Que signifient ces modèles de croissance ?
"Comptons pour 11 millions la population de la Grande-Bretagne et supposons que le produit actuel de son sol suffit pour la maintenir. Au bout de vingt-cinq ans, la population sera de 22 millions ; et la nourriture ayant également doublé, elle suffira encore à l'entretenir.[…] La race humaine croîtra selon la progression 1, 2, 4, 8, 16, 32, 64, 128, 256… tandis que les moyens de subsistance croîtront selon la progression 1, 2, 3, 4, 5, 6, 7, 8, 9 […]."
Thomas Robert Malthus, Essai sur le principe de population, 1798.
Modèle exponentiel
-
On s'intéresse en premier lieu à la croissance de la population humaine.
-
On appelle la population initiale de la Grande-Bretagne dans le raisonnement de Thomas Malthus. Quelle est la valeur (en millions) de ?
-
D'après le texte, 25 ans plus tard, la population est alors de 22 millions. On note cette valeur (en millions). Quelle semble être la relation mathématique entre et ?
-
Quel extrait du texte semble affirmer ou infirmer ce raisonnement ?
-
Toujours en suivant la logique de Malthus, quelle devrait être la valeur de ? Combien d'années se sont alors écoulées depuis la valeur initiale ?
On a a-priori ou alors
D'après le texte, la croissance humaine croît "selon la progression 1, 2, 4, 8, 16, 32, 64, 128, 256…" c'est-à-dire qu'elle subit effectivement une multiplication par deux au fil des périodes.
On multiplie la valeur précédente par deux : .
Deux périodes de 25 ans se sont écoulées, soit 50 ans.
-
-
On souhaite connaître l'évolution de cette suite en utilisant la calculatrice.
-

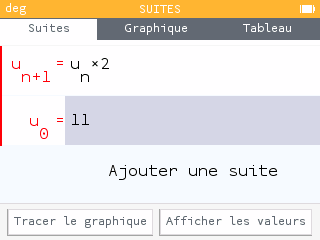
Pour calculer les termes suivants de la suite à l'aide de la calculatrice, il faut utiliser l'application Suites de la calculatrice. On sélectionne la cellule "Ajouter une suite" puis (récurrente d'ordre 1).
On attend en première ligne l'expression de en fonction de , soit . Quelle est la valeur de la raison dans le cas étudié ? En déduire l'expression à indiquer dans la calculatrice.
-
En seconde ligne, on attend la valeur initiale, c'est-à-dire la valeur du premier terme . Rappelez cette valeur dans notre exemple et compléter la formule sur votre calculatrice.
-
L'onglet Graphique permet d'obtenir une représentation graphique des différents termes de la suite. On peut zoomer sur l'écran avec la touche +, dézoomer avec la touche - et naviguer sur l'écran après avoir sélectionné la cellule "Naviguer".
Que peut-on dire sur l'évolution de cette suite numérique ?
-
Les valeurs des différents termes de la suite sont indiqués en bas de l'écran. Ces valeurs sont aussi rassemblées dans un tableau dans l'onglet du même nom. Quelle est la valeur de ? Combien d'années se sont alors écoulées depuis la valeur initiale ? Que penser de cette prévision ?
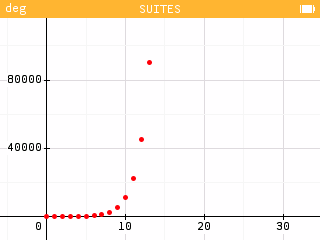
La croissance de la suite est de plus en plus rapide.
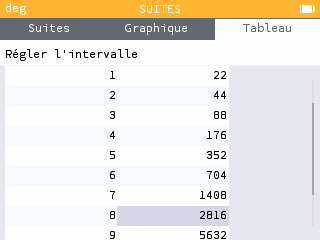
En suivant le modèle de Malthus, la population comptera 2816 millions d'individus au bout de 8 périodes de 25 ans, c'est-à-dire au bout de 200 ans, ce qui nous emmène environ à notre époque. On constate que ce modèle n'est pas du tout correct !
-
Lorsqu'il est question d'une suite de nombres liés les uns aux autres par une multiplication par un même réel, on parle alors de suite géométrique.
Soit le rang d'un nombre dans la suite numérique, le rang du nombre qui le suit immédiatement et le réel qui, multiplié, permet de passer de l'un à l'autre (et que l'on appelle raison). La relation qui relie ces termes est donc de type :
Ce type de modèle mathématique, suivant une suite géométrique, est appelé modèle exponentiel.

Modèle linéaire
-
Pour Mathus, la croissance de la population brittanique suit un modèle exponentiel tandis que l'évolution des ressources suit, elle, un modèle linéaire.
Retrouver dans le texte la signification d'un tel modèle. Quel type d'opération mathématique permet de passer d'un nombre à l'autre ? Quelle est la différence avec le modèle précédent ?
-
Dans l'explication de Malthus, les ressources initiales sont suffisantes pour assurer la subsistance de la population, on pose donc . Une période plus tard, on a . Quelle relation mathématique existe-t-il entre ces deux termes ? Attention au type d'opération mathématique à utiliser ici !
-
En utilisant les réponses précédentes, en déduire les informations à indiquer dans la calculatrice pour ajouter cette suite dans l'application (sans supprimer l'autre). Que peut-on dire sur sa représentation graphique, comparativement au modèle précédent ?
-
Dans quelle quantité se trouveront les ressources au bout de 200 ans ?
-
En déduire pourquoi Malthus décrit une catastrophe démographique. Avait-il raison ? Pourquoi ?
-
Les modèles mathématiques sont-il toujours exacts ?
D'après Malthus, "les moyens de subsistance croîtront selon la progression 1, 2, 3, 4, 5, 6, 7, 8, 9 […]."
C'est l'addition d'un même nombre qui permet ici de passer d'un terme à l'autre, tandis que dans le modèle précédent on procédait à une multiplication.
Ici, on a car on a vu que dans le modèle linéaire, on procédait à une addition pour passer d'un terme à l'autre.
Lorsqu'il est question d'une suite de nombres liés les uns aux autres par une addition par un même réel, on parle alors de suite arithmétique.
Soit le rang d'un nombre dans la suite numérique, le rang du nombre qui le suit immédiatement et le réel qui, additionné, permet de passer de l'un à l'autre (et que l'on appelle raison). La relation qui relie ces termes est donc de type :

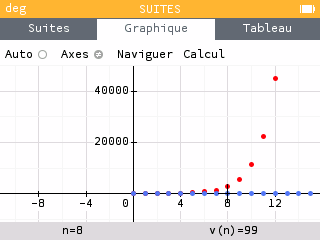
La croissance de la suite est moins rapide que la précédente. Les points sont alignés sur le graphique.
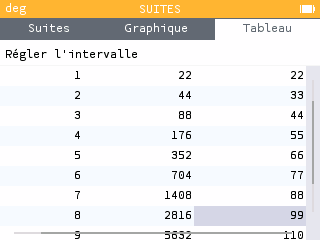
Dans 200 ans, c'est-à-dire à , les ressources seront égales à 99 millions.
Si l'on suit le raisonnement de Malthus, la population croît beaucoup plus vite que ses ressources, qui vont donc finir par manquer.
La crise qu'attendait Malthus n'est pas arrivée, bien au contraire, car, d'une part, la révolution industrielle a favorisé le développement de nombreux pays occidentaux et donc augmenté les moyens de production, et d'autre part, la croissance démographique n'a pas suivi le modèle exponentiel annoncé.
Pas toujours, comme on l'a vu ici ! Mais leur ambition est d'être le plus proche possible de la réalité. Ils sont utiles pour décrire plus simplement les données observationnelles et tenter de prédire les données à venir mais ils sont soumis à de nombreux paramètres. Ils sont aussi sujets à révision afin de mieux prendre en compte l'évolution de ces différents paramètres et préciser les résultats ! On peut prendre l'exemple des différents scénarios climatiques du GIEC qui reposent sur plusieurs profils d'évolution des gaz à effet de serre.
Mais heureusement, les progrès de la science et de l'informatique permettent aux modèles mathématiques d'être aujourd'hui bien plus fiables que les prédictions de Malthus !