Boîtes de conserve
Etude de fonction Dérivation Suites numériques
Objectif
Problème d'optimisation avec étude de fonction puis comparaison de deux suites numériques.
Une histoire de boîte
On souhaite fabriquer en aluminium une boîte de conserve d'un volume de 500 cm3 de manière à ce que la surface d'aluminium utilisée pour réaliser cette boîte soit minimale.
On modélise la boîte de conserve par un cylindre de hauteur et de base de rayon .
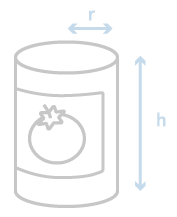
-
Calculer l'aire d'aluminium nécessaire si . On arrondira le résultat à l'entier.
-
Exprimer la hauteur de la boîte en fonction du rayon du cylindre. En déduire que l'expression de la surface en aluminium est égale à
-
Tracer sur la calculatrice la courbe représentative de la fonction définie pour tout réel . Donner une valeur approchée à 10-2 près de la valeur de pour laquelle la fonction est minimale.
-
La fonction est dérivable pour tout . Calculer sa dérivée et en déduire la valeur exacte de pour que la fonction soit minimale.
-
Quelles sont les dimensions (à 10-1 près) du cylindre ? Quelle est alors la surface d'aluminium nécessaire à sa fabrication ?
Si , alors d'où .
La surface nécessaire est égale à l'aire des deux disques (dessus et dessous) à laquelle on ajoute l'aire du rectangle qui forme le tube, soit ici :
D'où
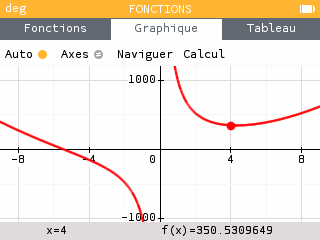
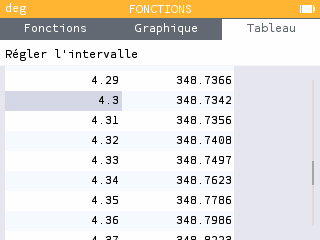
Lorsque la fonction admet un minimum local, la dérivée est nulle. On cherche donc tel que :
Il est possible de stocker la valeur exacte trouvée précédemment dans une variable A. Puis, grâce à la boîte à outils toolbox, on applique la fonction définie précédemment à notre variable A pour trouver la surface d'aluminium minimale.
On peut calculer la hauteur de la boîte de la même manière, on obtient environ 8,6 cm.

Une histoire d'alu
On décide finalement de fixer et . On veut fabriquer 30 000 boîtes.
On découpera les formes en aluminium dans un rectangle en les répartissant de façon suivante :
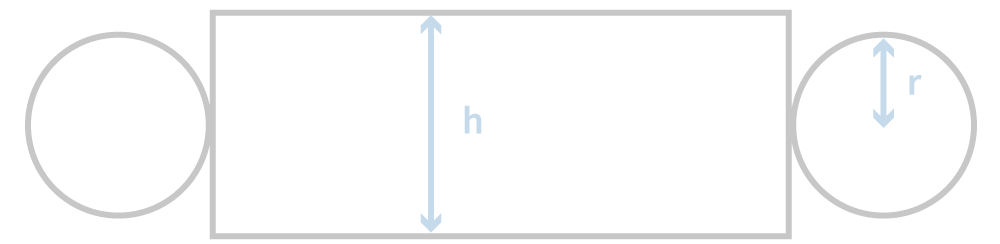
On hésite entre deux fournisseurs pour passer commande : le fournisseur S'alu propose de payer un forfait fixe de 15 000€ puis facture à 42€ le mètre carré. Son concurrent, Alu'minime facture à 55€ le mètre carré.
Lequel de ces deux fournisseurs est le plus intéressant pour notre commande ? Combien faut-il de centaines de mètres carré pour que les prix de la société S'alu deviennent plus attractifs ? On pourra procéder à quelques arrondis pour faciliter les prévisions.
On commence par calculer les dimensions du rectangle d'aluminium dans lequel seront découpées les formes, que l'on multiplie par le nombre de boîtes à fabriquer. Le rectangle qui forme le tube admet pour longueur la circonférence des disques, soit environ 26 cm.
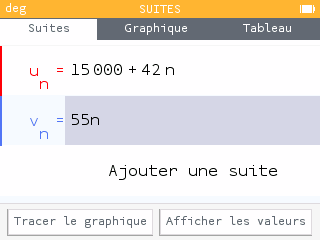
On utilise ensuite l'application Suites de la calculatrice pour entrer les suites correspondant au tarif de chacun des fournisseurs : et .
La société S'alu est plus intéressante dans notre cas. Elle est globalement plus intéressante lorsque l'on achète plus de 1200 m2.
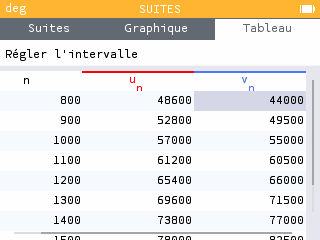
On peut bien sûr déterminer plus exactement par le calcul la valeur de pour laquelle : on trouve . C'est donc au 1154ème mètre carré que la première offre devient plus intéressante.
Une histoire à dormir debout !
On décide de tester un concept révolutionnaire de boîte en alu à couvercle cartonné. Il ne faut donc plus fabriquer qu'un seul disque en aluminium. Les dimensions de notre boîte vont-elles changer ?
La surface d'aluminium utilisée n'est plus que de dont le minimum est atteint en soit environ 5,42 cm. La hauteur est alors environ de 5,42 cm aussi.
Le rectangle dans lequel seront découpées les formes aura donc pour dimension environ 11 cm sur 34 cm, soit 1122 m2. Le second fournisseur sera donc cette fois plus intéressant !