Datation archéologique (fonction exponentielle)

Le carbone 14 est un isotope radioactif utilisé en archéologie pour dater des échantillons carbonés. En effet, celui-ci est présent dans toute matière organique vivante en proportion constante. A la mort de l'organisme, en l'absence d'échanges avec l'environnement, le nombre d'atomes de carbone 14 diminue selon une loi mathématique connue. La datation consiste à examiner le nombre d'atomes radioactifs présents dans l'échantillon à un instant $t$ et à le comparer au nombre initial d'atomes de carbone 14.

1. On note $N \left( t \right)$ la fonction mathématique qui au temps écoulé $t \left( t \geq 0 \right)$, exprimé en milliers d'années, associe le nombre de noyaux radioactifs présents dans l'échantillon. Cette fonction est définie sur l'intervalle $\lbrack 0;+\infty \lbrack$ par la relation :

   $N \left( t \right) = N_{0} \,\mathrm{e}^ {- 0,12 t}$

   1. On appelle temps de demi-vie $\displaystyle t_\frac{1}{2}$ le temps au bout duquel le nombre de noyaux radioactifs a diminué de moitié, soit $N\left( t_{\frac{1}{2}} \right) = \frac{N_{0}}{2}$.

      D'après les informations précédentes, démontrer que :

      $\displaystyle \mathrm{e}^ {-0,12 \, t_{1/2}} = \frac{1}{2}$

      $\displaystyle N\left( t_{\frac{1}{2}} \right) = N_{0} \,\mathrm{e}^ {- 0,12 \, t_{1/2}}=\frac{N_{0}}{2} \iff \mathrm{e}^ {-0,12 \, t_{1/2}} = \frac{1}{2}$

   2. On appelle $f$ la fonction définie sur $\lbrack 0 ; +\infty \lbrack$ par $f \left( x \right) = \mathrm{e}^{-0,12 \, x}$. Dresser son tableau de variation. D'après ce tableau, combien l'équation précédente compte-t-elle de solutions ?

      On calcule $f' \left( x \right) = -0,12 f \left( x \right)$.

      La fonction est strictement décroissante, de 1 vers 0. Elle passe donc une fois par 0,5 (on peut introduire le théorème des valeurs intermédiaires).

   3. A l'aide de l'outil Tableau (application Fonctions) de la calculatrice, donner une valeur approchée de $t_{\frac{1}{2}}$ à $10^{-1}$ près et proposer une interprétation de ce nombre.

      

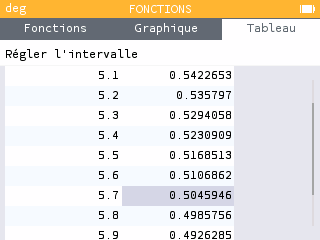
      $\displaystyle t_{\frac{1}{2}}$ est compris entre 5,7 et 5,8. Cela signifie qu'il faut entre 5700 et 5800 ans pour que le nombre de noyaux radioactifs diminue de moitié.

2. 1. Dans un échantillon organique vivant, on sait qu'on a 1 300 milliards d'atomes de carbone 12 pour un atome de carbone 14. Exprimer le rapport C14/C12.

      $\displaystyle \frac{C_{14}}{C_{12}} = 1,3 \times 10^{-12}$

   2. En déduire le nombre d'atomes de carbone 14 dans un échantillon contenant $7,7 \times 10^{17}$ atomes de carbone. On arrondira le résultat.

      $\displaystyle C_{14} = 1,3 \times 10^{-12} \times C_{12} = 1,0 \times 10^{6}$

3. 1. On considère un échantillon radioactif contenant initialement $1,0 \times 10^{6}$ atomes radioactifs. Combien reste-t-il de noyaux radioactifs au bout de 10 000 ans ? On donnera un résultat approché.

      

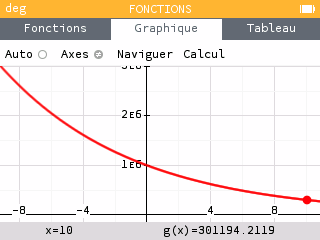
      D'après la question 1, la fonction est de la forme $N \left( t \right) = N_{0} \mathrm{e}^{-0,12 t}$ avec $N_{0}=10^{6}$. On étudie donc une fonction définie sur l'intervalle $\lbrack 0 ; +\infty \lbrack$ par $g \left( x \right) = 10^{6} \mathrm{e}^{-0,12 x}$. On rappelle que $t$ est exprimé en milliers d'années.

      Au bout de 10 000 ans, il reste environ 300 000 atomes radioactifs.

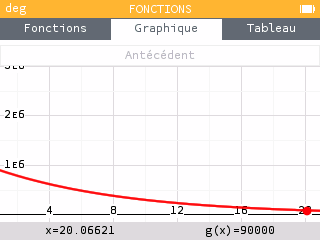
   2. On retrouve un os dans lequel on compte environ 90 000 atomes radioactifs. Estimer approximativement l'âge de cet os à l'aide de la calculatrice.

      A l'aide de la calculatrice, on cherche l'antécédent de 90 000 par la fonction définie précédemment.

      L'échantillon est âgé d'environ 20 000 ans.