Flocon de Koch

La fractale est un objet mathématique basé sur la répétition. Sa structure est identique, quelle que soit l'échelle à laquelle on l'observe.

Certaines fractales sont bien connues. On a par exemple l'ensemble de Mandelbrot, donc le script se trouve par défaut sur la calculatrice NumWorks. Le flocon de Koch est l'une de ces fractales très populaires et dont la réalisation est simple à comprendre. Elle repose sur une série d'instructions que l'on peut répéter à l'infini :

• Couper un segment en trois parties
• Construire un triangle équilatéral sur la partie centrale du segment, dont on ne conservera pas la base

Flocon de Koch et suites numériques

1. On veut modéliser le nombre de segments se trouvant sur une ligne du flocon (comme montré précédemment sur la figure) par une suite $u_n$.

   1. A l'état initial $n=0$, on ne dispose que d'un seul segment horizontal. Quelle est la valeur de $u_1$ (qui correspond au dessin de gauche sur la figure) ?

   On a $u_0=1$ et $u_1=4$.

   2. Quelle est la relation de récurrence entre $u_n$ et $u_{n+1}$ ?

   $u_{n+1}=u_{n} \times 4$

   3. En déduire la formule explicite de la suite $u_n$.

   $u_n=4^n$

2. On s'intéresse maintenant à la longueur de chacun de ces segments.

   1. Soit $l$ la longueur du segment d'origine. On donne $l=3$. Quelle est la longueur d'un segment après la première itération ?

   Après la première itération, chaque segment mesure $\displaystyle\frac{l}{3} = 1$.

   2. On note $v_n$ la suite qui modélise la longueur d'un segment au bout de $n$ itérations. Quelle est la relation de récurrence entre $v_{n+1}$ et $v_n$ ? En déduire une expression de $v_n$.

   On a $\displaystyle v_{n+1}=\frac{v_n}{3}$ avec $v_0=3$, d'où $v_n=\displaystyle 3 \times \left(\frac{1}{3}\right)^n = 3^{1-n}$

3. On souhaite maintenant s'intéresser à la longueur totale du côté du flocon après $n$ itérations.

   1. On appelle $w_n$ la suite associée à cette longueur. Exprimer $w_n$ en fonction de $u_n$ et $v_n$.

   $w_n=u_n \times v_n$

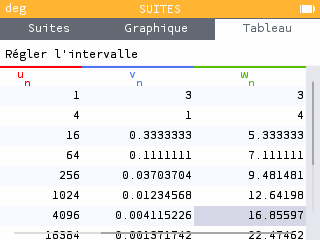
   2. On rappelle que $u_0=1$ et $v_0=3$. A l'aide de l'application Suites, faire apparaître le tableau de valeurs des trois suites entre 0 et 15. Quelle conjecture peut-on faire sur la convergence de $w_n$ ?

   
   

   3. Démontrer cette conjecture.

   $\displaystyle w_n = u_n \times v_n = 4^n \times 3 \times \left(\frac{1}{3}\right)^n = 3 \times \left(\frac{4}{3}\right)^n$

   Il s'agit d'une suite géométrique de raison supérieure à 1. Elle tend donc vers l'infini.

4. Nous allons enfin nous intéresser à l'évolution de la surface située sous la courbe au fil des itérations.

   1. On considère un triangle équilatéral de côté $c$. Calculer son aire en fonction de $c$.

   Le triangle équilatéral de côté $c$ admet une hauteur de longueur $\displaystyle \frac{c\,\sqrt{2}}{3}$.

   Sa surface est donc égale à $\displaystyle \frac{c^2\,\sqrt{3}}{4}$.

   2. D'après l'étude précédente de la suite $u_n$, établir que l'aire de chacun des triangles formés à chaque itération évolue selon une suite géométrique de raison $\displaystyle\frac{1}{9}$.

   A chaque itération, la longueur d'un segment est multipliée par $\displaystyle \frac{1}{3}$. L'aire d'un triangle est donc multipliée par $\displaystyle \frac{1}{9}$.

   3. On appelle $a_n$ l'aire formée par l'ensemble des triangles apparaissant à chaque itération sous la courbe, pour $n \geq 1$. D'après les questions précédentes, exprimer $a_{n+1}$ en fonction de $a_n$ et montrer qu'il s'agit d'une suite géométrique.

   A chaque itération, il apparaît 4 fois plus de triangles (suite $v_n$) dont l'aire est 9 fois plus petite. D'où, pour tout $n \geq 1$ :

   $\displaystyle a_{n+1}= \frac{4}{9} a_n$

   Il s'agit bien de la définition d'une suite géométrique de raison $\displaystyle\frac{4}{9}$.

   4. On rappelle que l'aire contenue sous le triangle à $n=1$ est égale à $\displaystyle\frac{\sqrt{3}}{4}$. En déduire l'aire se trouvant sous la courbe après $n$ itérations lorsque $n$ tend vers l'infini.

   On sait que l'aire contenue sous la courbe est la somme des $a_n$ apparaissant à chaque itération. On utilise la formule de la somme des termes consécutifs d'une suite géométrique :

   $\displaystyle A = \frac{\sqrt{3}}{4}\times\frac{1-\left(\frac{4}{9}\right)^{n-1}}{1-\frac{4}{9}} = \frac{\sqrt{3}}{4} \times \frac{9}{5} \times \left( 1- \left(\frac{4}{9} \right)^{n-1} \right)$

   Lorsque $n$ tend vers l'infini, la suite tend vers $\displaystyle \frac{9\sqrt{3}}{20}$.

5. Que peut-on dire sur la convergence des suites $w_n$ et $a_n$ ? Quelle est la particularité géométrique de cette fractale ?

La suite $w_n$ est divergente, elle n'admet pas de limite finie, tandis que la suite $a_n$ est convergente.

Le flocon de Koch est un objet géométrique de longueur infinie dans un espace fini !

Programmer un flocon de Koch

Pour représenter graphiquement ce flocon de Koch à l'aide d'un programme, nous allons utiliser le module Turtle de la calculatrice qui permet de piloter une tortue à l'écran à l'aide d'instructions basiques.

Par défaut, la tortue démarre au centre de l'écran, tournée vers la droite. L'instruction forward(x) permet de faire avance la tortue de $x$ pixels. Les instructions left(a) et right(a) permettent de faire pivoter la tortue à gauche ou à droite de $a$ degrés.

1. Ecrire un programme permettant de tracer un côté du flocon de Koch après une itération. On utilisera une fonction cote(l), $l$ étant défini comme la longueur du segment initial.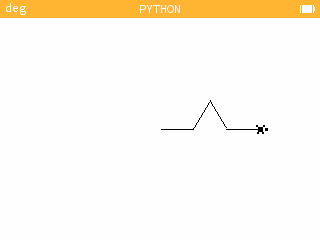

   

   On n'oubliera pas de faire précéder l'algorithme de la ligne from turtle import * qui permet d'importer toutes les fonctions du module Turtle.

from turtle import *
def cote(l):
  forward(l/3)
  left(60)
  forward(l/3)
  right(120)
  forward(l/3)
  left(60)
  forward(l/3)
        

2. On aimerait écrire une fonction qui permet de tracer le segment après $n$ itérations.

   Les mouvements utilisés sur cette première itération sont exactement identiques à chaque itération sur chaque segment. Nous allons donc utiliser la récursivité, un concept de programmation qui permet à une fonction de s'appeler elle-même.

   Ici, le bloc d'instruction que l'on souhaite répéter, et qui doit donc s'appeler lui-même correspond à la fonction que nous avons écrite précédemment.

   Compléter l'algorithme suivant :

   from turtle import *
   def cote(l,n):
     if n == 0:
       forward(l)
     else:
       cote(...,n-1)
       left(...)
       cote(...,n-1)
       right(...)
       cote(...,n-1)
       left(...)
       cote(...,n-1)
             

3. A quoi servent les instructions en ligne 3 et 4 ?

4. Ecrire une fonction flocon(l,n), faisant appel à la fonction définie précédemment et permettant de tracer le flocon dans sa totalité.



Un script est disponible sur cette page.

Les instructions en ligne 3 et 4 permettent d'arrêter la récursion. La fonction cesse de s'appeler elle-même.

On peut ensuite inciter à réaliser d'autres types de fractales en utilisant la récursivité, comme par exemple l'arbre de Pythagore.