Lancer de ballon
Second degré Système d'équations Variables aléatoires
Objectif
Manipulation de fonctions du second degré dans un premier temps, puis probabilités avec utilisation d'une variable aléatoire.
Yasmine a installé un nouveau jeu sur son téléphone portable pour passer le temps.
L'objectif est de parcourir les niveaux en réalisant des défis consistant à lancer des ballons avec des élastiques à travers les paysages.
Niveau 1 : Trajectoires paraboliques
Yasmine doit lancer un ballon depuis une hauteur de 50 cm et le faire atterrir dans une petite piscine 5 mètres plus loin en surmontant un obstacle de 2 m.
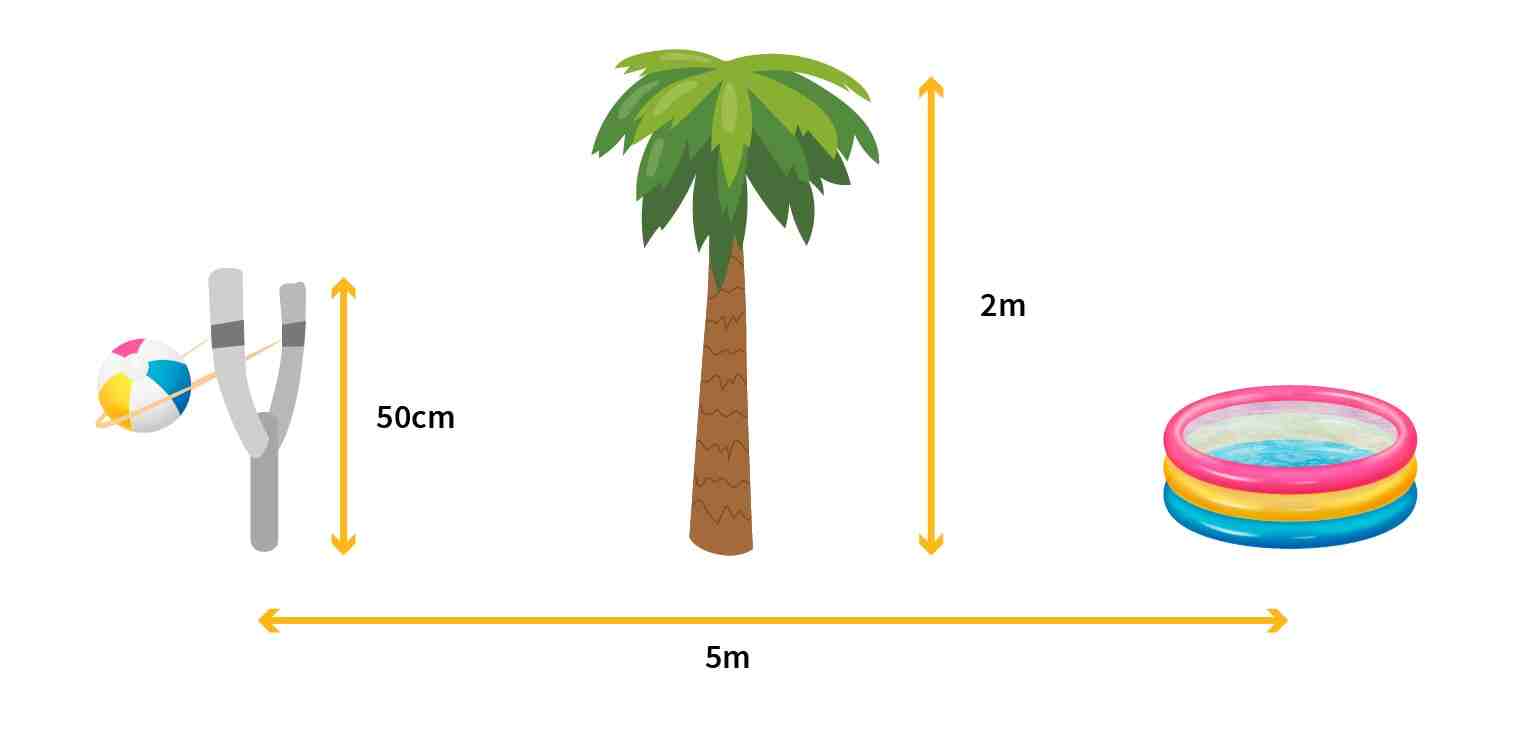
La trajectoire du ballon sera une parabole dont on cherche à déterminer l'équation pour optimiser le lancer.
-
Rappeler l'expression mathématique des fonctions dont la représentation graphique est une parabole.
-
On se place dans un repère tel que le ballon passe par le point de coordonnées (0 ; 0,5). Sans poser aucun calcul, que peut-on dire sur les signes de , et ?
-
Donner les coordonnées de trois points A, B et C se trouvant sur la parabole marquant la trajectoire idéale.
-
Déterminer l'expression de la fonction passant par ces trois points.
-
Zut, Yasmine a fait une mauvaise manipulation et n'est pas parvenue à optimiser sa parabole. La trajectoire empruntée admet l'équation suivante : .
Que va-t-il se passer ? Yasmine peut-elle atteindre son objectif ? Pour simplifier les choses, le jeu considère que la cible est atteinte lorsque le ballon atterrit à moins d'1 mètre du centre de la piscine.
-
Nouvel essai. Yasmine tire sur l'élastique et emmène son ballon au point D de coordonnées en visant le sommet de l'arbre. Atteint-elle son but ? On pourra arrondir les valeurs à 10-2 près pour faciliter les calculs.
Une parabole est la représentation graphique d'une fonction du second degré de la forme .
La parabole est ouverte vers le bas donc est négatif. La courbe croise l'axe des ordonnées au-dessus de zéro, donc est positif. La parabole admet son sommet à droite de l'axe des ordonnées donc est aussi positif.
Le point A correspond à l'intersection de la parabole avec l'axe des ordonnées. Ses coordonnées sont données : .
Le point B correspond au sommet de la parabole que l'on considère comme étant le sommet de l'arbre (mais on peut bien sûr viser plus haut !). Ses coordonnées sont donc .
Le dernier point C correspond à la position de l'objectif, à l'intersection avec l'axe des abscisses. Ses coordonnées sont donc .
On cherche à déterminer les réels , et tels que :


La résolution du système d'équations nous donne .
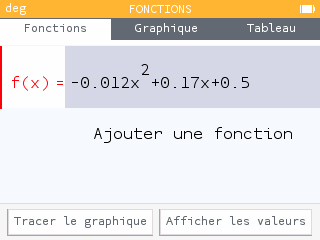
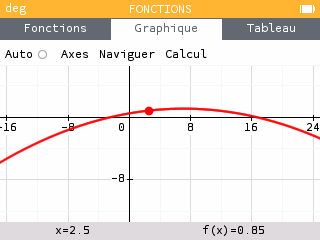
La trajectoire est trop basse, le ballon va se cogner dans l'arbre !
On peut réutiliser les points A et B précédemment définis. Cependant ici, nous utiliserons le point D pour établir le système d'équation.
On cherche à déterminer les réels , et tels que :


La résolution du système d'équation nous donne .
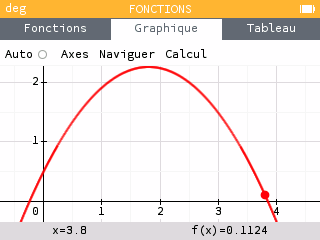

On cherche les racines de cette équation du second degré et on obtient 3,85 : la cible sera manquée à 15 cm près !
Niveau 2 : Viser la cible
Après de multiples essais, Yasmine est parvenue aux niveaux suivants. Elle s'interroge maintenant sur l'un des défis qu'elle doit relever.
Yasmine doit lancer trois ballons sur une cible. La cible est divisée en plusieurs segments rapportant chacun un certain nombre de points. L'objectif est d'obtenir suffisamment de points pour aller au niveau suivant.
-
Yasmine atteint ce type de cible en moyenne 8 fois sur 10. A l'aide d'un arbre de probabilités, déterminer la probabilité qu'elle atteigne la cible trois fois de suite.
-
Quelle est la probabilité qu'elle atteigne la cible seulement deux fois sur trois ?
-
La probabilité d'atteindre chacun des segments de la cible est liée à la surface de ce segment par rapport à la totalité de la cible. Par exemple, un segment couvrant 30% de la cible est atteint avec une probabilité de de 0,3 sachant que la cible est touchée.
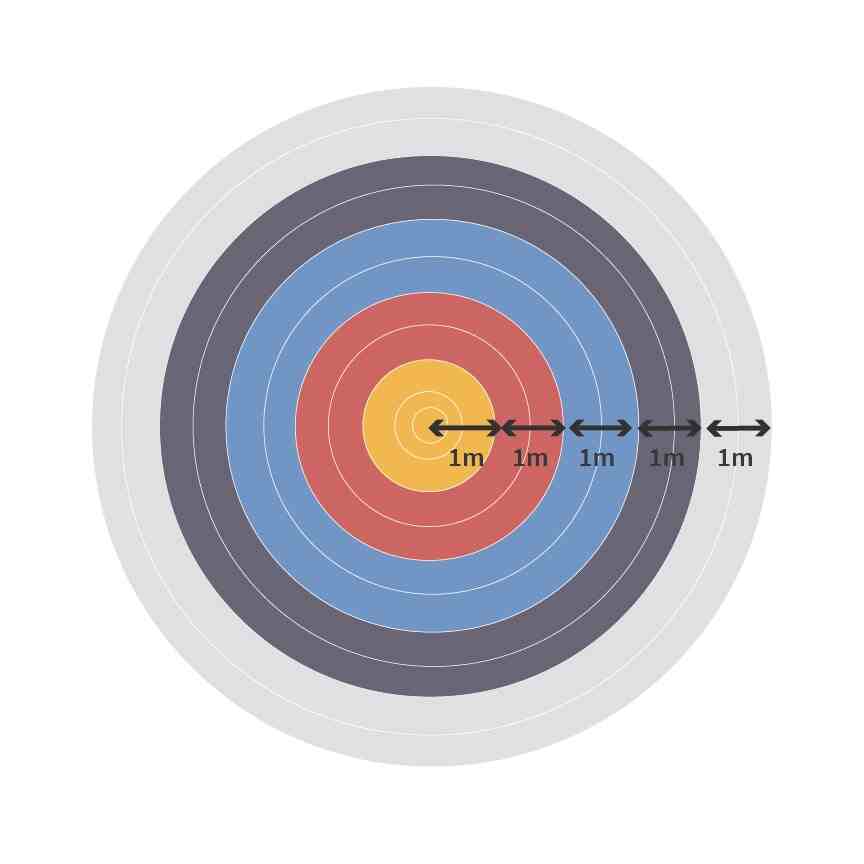
La partie jaune de la cible rapporte 10 points, la partie rouge 4 points, la partie bleue 3 points, la partie noire 2 points, la partie blanche 1 point. Si la cible n'est pas atteinte, on perd 1 point.
Pour atteindre le niveau suivant, Yasmine doit obtenir 5 points en trois lancers.
Pour Yasmine, le jeu semble irréalisable ! Qu'en pensez-vous ? On notera X la variable aléatoire associée au nombre de points obtenus à l'issue d'un lancer.
La partie jaune de la cible admet 1m de rayon, sa surface est donc égale à . La partie rouge admet 2m de rayon, la surface est donc de auxquels on soustrait la surface jaune, soit . On fait les mêmes calculs pour les autres sections et on obtient pour le bleu, pour le noir et pour le blanc.
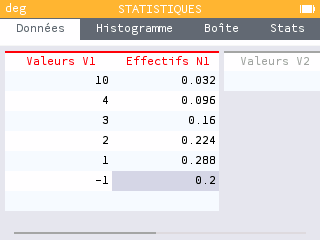
La partie jaune représente donc de la cible, dont la probabilité d'être touchée est de 0,8. D'où .
La partie rouge représente de la cible, d'où .
La partie bleue représente de la cible, d'où .
La partie noire représente de la cible, d'où .
La partie blanche représente de la cible, d'où .
Et bien sûr, la probabilité de ne pas toucher la cible est de 0,2 d'où .
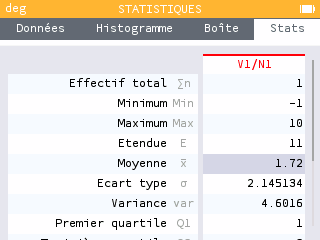
L'espérance mathématique de X est égale à 1,72 pour un lancer, soit un peu plus de 5 pour trois lancers. Le jeu semble tout à fait faisable !