Le jeu des allumettes

Le jeu des allumettes se joue à deux. On dispose sur la table vingt allumettes les unes à côté des autres. Tour à tour, les deux joueurs doivent prendre entre 1 et 3 allumettes parmi celles disposées sur la table. Celui qui prend la dernière allumette a perdu.

Programmer le jeu

Nous allons commencer par jouer contre un ordinateur qui, dans un premier temps, joue complètement au hasard.

On propose de télécharger le script suivant et d'analyser ensemble le code.

1. A quoi sert le module random importé dès la deuxième ligne ?

Etant donné que l'ordinateur va jouer au hasard, il va générer un entier aléatoire compris entre 1 et 3 (correspond au nombre d'allumettes à enlever) à l'aide de la commande randint(1,3) qui est compris dans le module random, qu'il faut donc importer en début de script.

2. Qui commence à jouer ? Peut-on distinguer la partie du code où c'est l'ordinateur qui joue, et celle où il s'agit du joueur ?

C'est le joueur qui commence à jouer puisque le programme débute avec l'affichage "Choisir un nb entre 1 et 3:" qui permet de définir une variable appelée sub. La première partie du code correspond plutôt au tour du joueur, alors que celle de l'IA commence plutôt après le else, qui marque le cas dans lequel le joueur n'a pas réalisé un coup gagnant. Le nombre d'allumettes que l'ordinateur enlève correspond à une variable nommée ia.

3. Expliquer comment s'effectue la suppression des allumettes à chacun des tours des joueurs.

La ligne allumettes.remove(allumettes[-1]) permet d'enlever l'élément de rang -1 dans la liste allumettes, autrement dit le dernier élément de la liste. Cette ligne est répétée autant de fois que le nombre qui a été entré par l'utilisateur ou par l'ordinateur à l'aide d'une boucle.

4. Expliquer la précision indiquée en second argument dans la ligne ia=randint(1,3 if len(allumettes)>3 else len(allumettes)-1)

S'il reste trois allumettes ou moins, l'ordinateur ne doit pas pouvoir enlever davantage d'allumettes qu'il en reste en jeu, ni enlever la dernière car il aurait automatiquement perdu. On souhaite qu'il reste toujours une allumette sur le plateau à la fin pour signifier la victoire de l'un ou de l'autre.

Faites plusieurs parties et voyez si vous parvenez à gagner contre l'ordinateur !

Envisager la stratégie gagnante

Prenons maintenant l'exemple d'un joueur qui ne prévoit pas ses premiers coups, mais qui ne laissera pas l'occasion s'envoler si l'on commet une erreur lors du dernier tour.

1. L'objectif est donc de faire en sorte qu'à la fin d'un de nos tours, il ne reste plus qu'une seule allumette sur la table, que prendra l'adversaire. Pourquoi gagnera-t-on à coup sûr si l'on laisse cinq allumettes à l'adversaire à la fin de notre tour ?

On peut raisonner en tatônnant. Si à la fin de notre tour, il reste 4 allumettes ou moins, l'adversaire va évidemment identifier le nombre d'allumettes à prendre pour gagner.

En revanche, s'il reste cinq allumettes sur la table à la fin de notre tour, l'adversaire ne pourra pas gagner si l'on joue correctement : s'il prend 1 allumette, nous en prendrons 3 ; s'il en prend 2, nous en prendrons 2 ; et s'il en prend trois, nous n'en prendrons qu'une pour gagner. Dans tous les cas, il s'agit d'une position gagnante : il faut laisser cinq allumettes en jeu à la fin de son propre tour.

Pour six allumettes ou plus, on risque en revanche de se retrouver dans la position où c'est l'adversaire qui parvient à avoir 5 allumettes en jeu à la fin de son tour et nous avons vu que c'était une position gagnante.



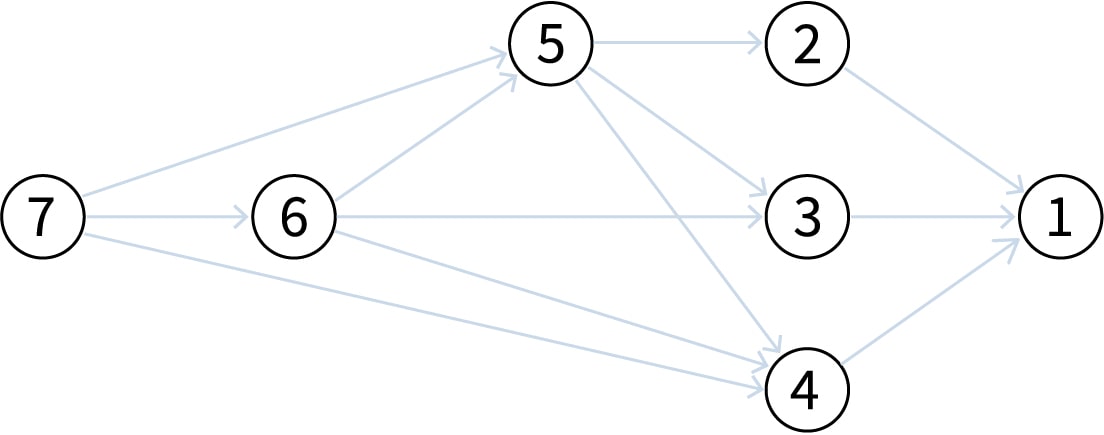
On peut dessiner un extrait du graphe orienté correspondant au jeu pour s'en convaincre. On part du principe que le dernier coup, s'il est évident, sera joué : 2, 3 ou 4 vers 1. Toutes les chaînes partant de 5 atteignent 1 et sont de longueur 2.

2. En raisonnant de la même façon, combien faut-il laisser d'allumettes sur la table à la fin de son tour pour être sûr d'en laisser cinq à l'adversaire au tour d'après ?

De la même manière, si l'on laisse neuf allumettes sur la table, on est assuré de gagner : si l'adversaire en prend une, on en prend trois ; si l'adversaire en prend deux, on en prend aussi deux ; et si l'adversaire prend trois allumettes, on n'en prendra qu'une seule.

3. Identifier ainsi les "nombres-clés" d'allumettes à laisser sur la table pour l'adversaire. Vaut-il donc mieux commencer ou laisser l'adversaire commencer ?

Si l'on veut contrôler la partie, il faudra laisser à l'adversaire : 5, 9, 13 et 17. Si celui qui commence la partie connaît la stratégie à appliquer, il est sûr de gagner ! Il lui faudra commencer en enlevant 3 allumettes.

4. Mettez la théorie en pratique en rejouant au jeu scripté de la première partie. Réussissez-vous à gagner à tous les coups ?

Programmer la stratégie gagnante

On aimerait modifier le programme ci-dessus de manière à ce que l'ordinateur ne joue plus au hasard, mais applique la stratégie gagnante tout en laissant commencer le joueur… Histoire de lui laisser une chance de s'en sortir !

1. Le comportement de l'ordinateur ne va donc plus être laissé au hasard, mais dépendre directement du nombre d'allumettes en jeu pour appliquer la bonne stratégie.

   Quelle est donc la partie du programme à modifier ?

La seule partie du programme à modifier concerne la variable ia. Dans le premier programme, sa valeur était déterminée aléatoirement. Dans celui-ci, sa valeur ne doit plus être laissée au hasard.

2. On distingue les situations dans lesquelles le nombre d'allumettes restant sur la table à la fin du tour du joueur est un multiple de 4. Comment doit réagir l'ordinateur ? Quelle ligne de code correspond à ce cas ?

Pour atteindre une position gagnante, si le nombre d'allumettes est un multiple de 4 avant le tour de l'ordinateur, il faudra impérativement enlever trois allumettes. Par exemple, si 16 allumettes sont en jeu, l'ordinateur va en enlever trois pour terminer son tour sur 13, qui est une position gagnante.

if len(allumettes)%4==0: ia=3

3. Distinguer ainsi les autres situations possibles et proposer la ligne de code correspondante. Dans le cas où c'est le joueur qui est dans une position gagnante, on suggère que la machine n'enlève qu'une seule allumette, pour "temporiser" en espérant une erreur du joueur, ou bien que le nombre d'allumettes soit à nouveau le fruit du hasard, pour éviter que la stratégie à adopter pour gagner contre la machine ne soit toujours la même.

Le script est disponible à cette adresse.

4. Que se passerait-il s'il y avait 21 allumettes en jeu au début de la partie ?

S'il y avait 21 allumettes en jeu, alors le joueur ne pourrait pas gagner contre l'ordinateur. En effet, cela place la machine dans une position gagnante dès le début de la partie : quel que soit le nombre d'allumettes qu'enlèvera le joueur, l'ordinateur fera en sorte qu'il en reste 17 à la fin de son tour.

Pour aller plus loin

Avec un peu de patience, on peut utiliser Kandinsky pour remplacer nos listes de "l" par des allumettes un peu plus réalistes !



Un script est disponible à cette adresse.

Dans ce script, le raisonnement est un peu à l'inverse de celui qu'on a suivi plus haut : on compte non plus le nombre d'allumettes en jeu, mais le nombre d'allumettes qui ont été supprimées. En effet, le script consiste à dessiner 20 allumettes en début de partie et à recouvrir en blanc celles qui ont été enlevées par l'un ou l'autre des joueurs. D'où un programme légèrement différent.