La planche de Galton

Contexte

En 2017, un jeu inspiré des Etats-Unis fait son apparition à la télévision française : "The Wall, face au mur". Dans ce jeu, les candidats doivent répondre à des questions de culture générale et leurs gains (ou pertes, en fonction de la réponse à la question) sont décidés par le hasard : une bille descend d'un mur de 12 mètres criblé de clous, faisant rebondir la bille ici et là, et atterrit dans un compartiment auquel est associée une somme d'argent.

Une vidéo de présentation de l'émission est accessible à cette adresse : Lien YouTube.

Le principe de ce mur géant rappelle le principe de la planche de Galton, invention d'un statisticien britannique du même nom.

En partant du cas simple de la planche de Galton, nous allons tenter de déterminer le gain moyen obtenu lors du jeu télévisé.

Planche de Galton

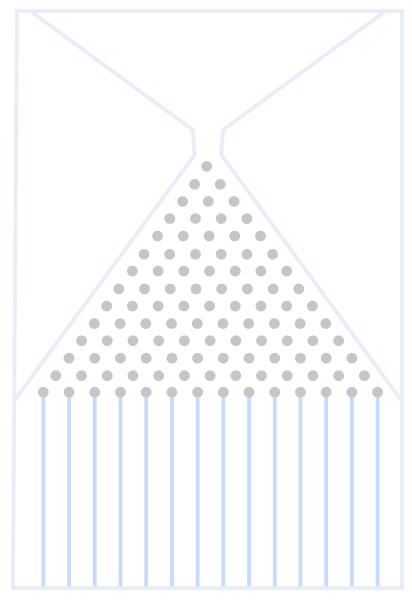
Une planche de Galton est composée de plusieurs rangées de clous positionnés de façon triangulaire (voir ci-contre). Ainsi, la n-ième rangée, par exemple, est composée de n clous. Le diamètre de la bille ainsi que l'écartement entre les clous sont choisis de façon à ce que, lorsque la bille tombe sur un clou, la probabilité qu'elle tombe à gauche est identique à la probabilité qu'elle tombe à droite.

Nous allons prendre l'exemple d'un planche de Galton composée de 10 rangées de clous.

1. Combien de compartiments se trouvent en bas de la planche ?

   La 10e rangée est composée de 10 clous. La bille peut tomber à gauche ou à droite de chacun de ces clous. Il y a donc 11 compartiments au bas de la planche.

2. Quelle est la probabilité que la bille tombe dans le compartiment le plus à gauche ?

   Si la bille tombe dans le compartiment le plus à gauche, cela signifie qu'à chacune des 10 rangées, la bille est tombée du côté gauche, ce qui arrive avec une probabilité de ½. Ainsi, la probabilité que la bille tombe dans le compartiment le plus à gauche est de $\left(\frac{1}{2}\right)^{10}$.

On note 0 le compartiment le plus à gauche, 1 le suivant et ainsi de suite. On pose $X$ comme étant la variable aléatoire associée à chacun des compartiments.

3. Pourquoi la position de la bille en bas du mur suit-elle une loi binomiale ? Quels sont ses paramètres ?

   Chaque chemin qu'emprunte la bille en arrivant sur un clou correspond à une expérience aléatoire dont l'issue est "gauche", ou "droite". Cette expérience aléatoire est répétée de manière indépendante pour chaque rangée. On note $X$ la variable aléatoire associée au nombre d'issues correspondant à "droite". Nous sommes donc dans un schéma de Bernoulli de paramètres $n = 10$ et $p = 1/2$.

4. A l'aide de l'outil Statistiques de la calculatrice, dresser un tableau de probabilité pour chacune des valeurs de la variable aléatoire. Que remarque-t-on ? Dans quel compartiment la bille tombe-t-elle le plus souvent ?

   

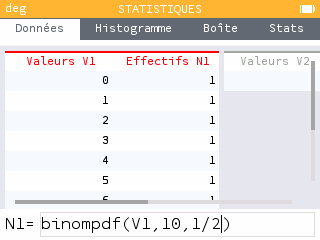
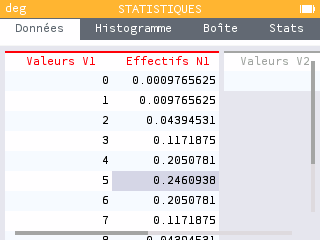
   Dans le menu Statistiques, la colonne V1 correspond aux valeurs de $X$ : on remplit donc la colonne avec des nombres de 0 à 10.

   Dans la colonne N1, on entre les résultats d'une loi binomiale de paramètres $n=10$ et $p=½$. Pour ce faire, sélectionner le nom de la colonne puis OK => Remplir avec une formule. Dans la Boîte à outils, sélectionner Probabilités > Lois de probabilités > Loi binomiale et remplir avec les valeurs souhaitées. Ici, $m$ prend la valeur V1.

   On remarque que les probabilités sont plus élevées pour les valeurs centrales. Le compartiment le plus souvent atteint est le n°5, soit celui du milieu. On peut alors interroger les élèves sur leur interprétation de ce phénomène.

   

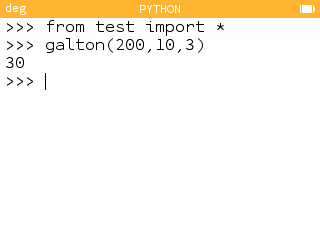
5. 1. Ecrire un algorithme en Python permettant de connaître le nombre de billes parmi $b$ tombées dans le compartiment $k$ d'une planche de Galton composée de $n$ rangées. On testera par exemple le nombre de billes contenues dans le compartiment n°3 sur 200 billes lâchées au départ sur une planche de Galton de 10 rangées.

      On pourra par exemple utiliser un compteur pour compter le nombre de chemins "gauche" ou "droite" empruntés par une bille, ces chemins étant empruntés aléatoirement à l'aide d'une fonction de type randint(0,1) qui retourne aléatoirement soit un 0, soit un 1.

      Ainsi, une bille ayant toujours emprunté le chemin "gauche" par une succession de 0 aléatoires finit dans le compartiment n°0. A l'inverse, une bille ayant emprunté 10 fois le chemin "droite" par une succession de 1 aléatoires finit dans le compartiment n°10.

      

      

      On pourra proposer aux élèves plus avancés de réaliser un programme plus complexe, permettant par exemple d'afficher dans une liste le nombre de billes dans chacun des compartiments à l'issue de l'expérience, voire même de les représenter graphiquement avec Kandinsky.

      

      

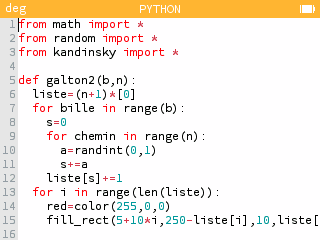
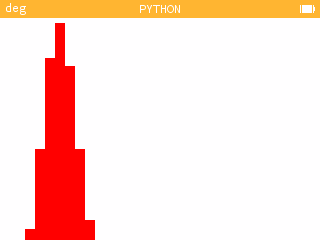
      Les scripts sont accessibles sur cette page.

   2. Tester les différents paramètres : Comment évolue le nombre de billes dans un compartiment donné si l'on augmente le nombre de rangées dans la planche ? Si l'on augmente le nombre de billes lancées au départ ? Pour une configuration donnée, quels sont les compartiments qui contiennent le plus de billes ?

      Plus le nombre de rangées augmente, plus les billes sont réparties sur l'ensemble des compartiments. Ainsi, le nombre de billes dans un compartiment donné diminue si l'on augmente le nombre de rangées. Si l'on augmente le nombre de billes de départ, le nombre de billes augmente bien sûr dans un compartiment donné, mais la proportion sur l'ensemble de billes lâchées reste identique.

      Pour tester leurs hypothèses, on peut proposer aux élèves de modifier légèrement le programme afin qu'il calcule non pas un nombre de billes, mais plutôt la fréquence obtenue.

Retour au "mur"

La planche de Galton de l'émission télévisée est légèrement différente. Composée de 14 rangées de clous, la bille peut être lancée lors de la première manche depuis trois positions différentes au sommet du mur : au centre ou à l'une des deux extrémités. En bas, les sommes allouées aux différents compartiments sont les suivantes :

Le candidat doit donc choisir la position de départ qui lui semble la plus propice à l'obtention du gain maximal.

Nous allons nous intéresser au gain que l'on peut espérer obtenir en partant de la position n°4, c'est-à-dire la position centrale, afin de rester dans une situation similaire à celle d'une planche de Galton de 14 rangées.

1. On note $Y$ la variable aléatoire associée au gain obtenu à l'issue d'un premier lancer de bille. Quelle est la loi de probabilité que suit $Y$ ?

   On peut reprendre la variable aléatoire $X$ définie dans la première partie dans le raisonnement, c'est-à-dire le nombre de fois où la bille prendra la direction "gauche" pour pouvoir réutiliser une loi binomiale de paramètres $n=14$ et $p=1/2$ directement dans la calculatrice.

   

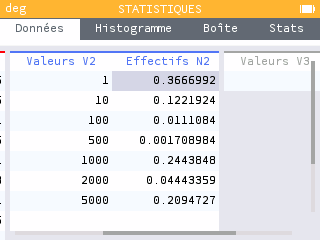
2. En moyenne, quelle somme peut-on espérer obtenir en lançant la bille depuis la position centrale ?

   

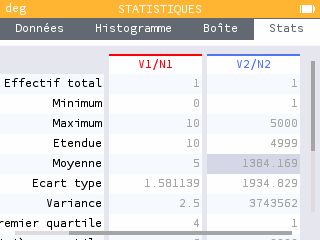
   On peut utiliser directement l'outil Stats de la calculatrice pour connaître l'espérance du gain.