Racine de deux par la méthode de Héron

L'existence des nombres irrationnels est connue depuis l'Antiquité. En effet, comment exprimer la longueur d'un carré de surface égale à 2 ?

La géométrie déborde d'exemples qui nécessitent l'utilisation de valeurs incommensurables à l'aide de simples entiers et de leurs quotients. Afin d'approcher la valeur de tels nombres, Héron d'Alexandrie, mathématicien grec du I^er siècle après J.-C., utilise un algorithme de calcul que nous allons étudier ici. Et si cette méthode de calcul porte le nom d'un mathématicien grec, elle était cependant très probablement connue des anciens Egyptiens.

Première approche avec utilisation de la calculatrice

On propose pour commencer d'utiliser la calculatrice afin de déterminer une première valeur approchée de $\sqrt{2}$.

Dans l'applications Fonctions, on entre la fonction $x^2-2=0$. On s'intéressera à la racine positive de l'équation $f\left(x\right)=0$.

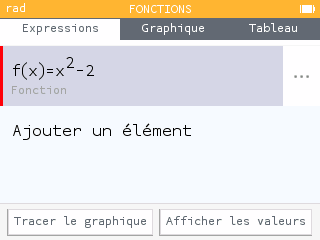
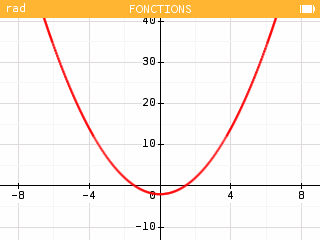
1. Grâce à l'onglet Tableau de l'application, déterminer deux entiers naturels consécutifs $a$ et $b$ encadrant la solution positive $x_0$ de l'équation $f\left(x\right)=0$. On pourra essayer de repérer entre quels entiers la valeur $f\left(x\right)$ change de signe.

Le tableau nous donne : $1<x_0<2$.

2. 

   

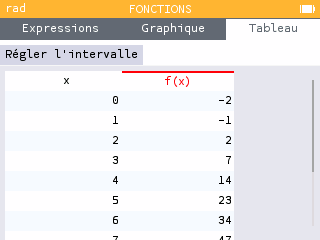
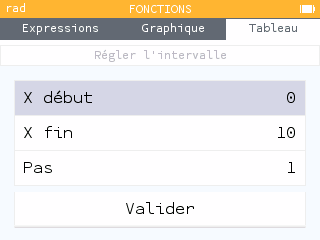
   Sélectionner maintenant la cellule "Régler l'intervalle". Entrer la valeur de $a$ pour "X début" et la valeur de $b$ pour "X fin". On règle ensuite le pas à 0,1 avant d'accéder de nouveau au tableau.

   Encadrer maintenant $x_0$ avec deux nombres décimaux d'amplitude 0,1.

On obtient $1,4<x_0<1,5$.

3. En utilisant à nouveau ce procédé, dit "par balayage", déteminer un encadrement d'amplitude 0,001 de $x_0$.

On obtient $1,41<x_0<1,42$ puis $1,414<x_0<1,415$.

Dans cette partie, nous avons procédé par encadrements successifs afin de nous rapprocher de la valeur de la racine. C'est dans cet esprit que se situe la méthode de Héron… mais sans calculatrice, bien évidemment !

Méthode de Héron : encadrer la racine avec des suites numériques

Le procédé de cet algorithme est très simple : prenons un rectangle de côtés 1 et 2. L'aire de ce rectangle est égale à 2. La racine de 2 correspond au côté du carré que l'on obtiendrait en déformant notre rectangle, mais en conservant sa surface égale à 2.

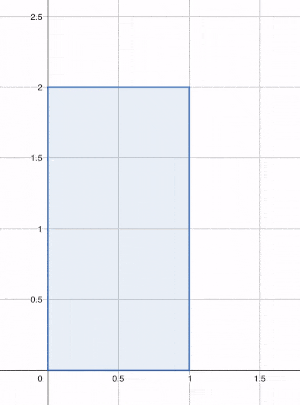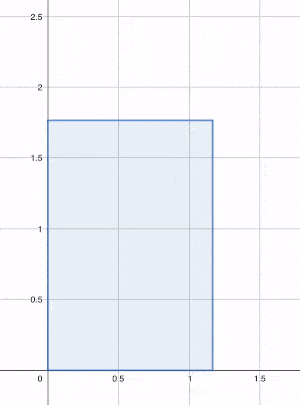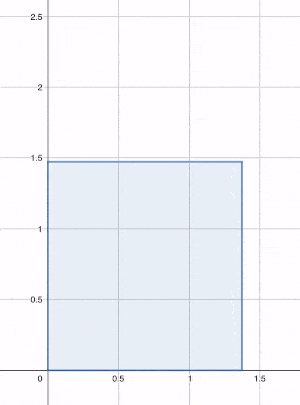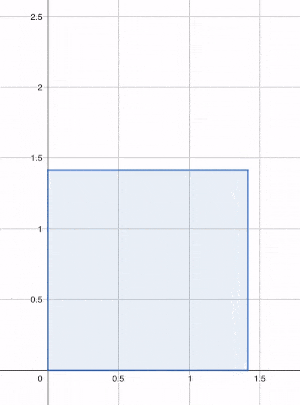
Héron propose donc de construire progressivement ce carré en partant de notre rectangle de côtés 1 et 2. On part donc d'un encadrement de $\sqrt{2}$ par deux nombres $a_1 = 1$ et $b_1 = 2$, correspondant respectivement à la largeur et à la longueur de notre rectangle, tels que $a_1 < \sqrt{2} < b_1$.

Notre objectif est de calculer des valeurs successives de $a$ et $b$, c'est-à-dire de la largeur et de la longueur d'un rectangle dont la forme se rapproche peu à peu du carré recherché.

1. Pour déterminer la valeur suivante de $b$, on réalise la moyenne de nos deux bornes, soit $\displaystyle b_2 = \frac{a_1+b_1}{2}$.

   1. Calculer la valeur exacte de $b_2$.

   $\displaystyle b_2 = \frac{a_1+b_1}{2} = \frac{3}{2}$

   2. En déduire la valeur exacte de $a_2$. On rappelle qu'il s'agit de la largeur d'un rectangle dont l'aire est égale à 2.

   On cherche $a_2$ tel que $a_2 \times b_2 = 2$, d'où :

   $\displaystyle a_2 = \frac{2}{b_2}=2\times\frac{2}{3}=\frac{4}{3}$

2. Procéder de la même façon pour calculer les valeurs exactes de $a_3$ et $b_3$.

On commence par définir $b_3$ comme étant la moyenne des deux valeurs précédentes :

$\displaystyle b_3=\frac{a_2+b_2}{2}=\frac{1}{2}\left(\frac{3}{2}+\frac{4}{3}\right) = \frac{17}{6}$

On calcule ensuite $a_3$ tel que $a_3 \times b_3 = 2$ :

$\displaystyle a_3 = \frac{2}{b_3} = 2 \times \frac{6}{17} = \frac{12}{17}$

3. Définir les suites définies par récurrence $\left(a_n\right)$ et $\left(b_n\right)$ qui correspondent à notre algorithme. On admet que ces deux suites sont strictement positives pour tout entier naturel $n>0$.

On définit pour tout entier naturel $n>0$ la suite $\left( a_n \right)$ telle que :

$\begin{cases} a_1=1 \\ \displaystyle a_{n+1}=\frac{2}{b_{n+1}}=\frac{4}{a_n+b_n} \end{cases}$

De même, on définit pour tout entier naturel $n>0$ la suite $\left( b_n \right)$ telle que :

$\begin{cases} b_1=2 \\ \displaystyle b_{n+1}=\frac{a_n+b_n}{2} \end{cases}$

4. Entrer ces deux suites dans la calculatrice. En examinant l'onglet Graphique, quelles hypothèses peut-on formuler sur leur sens de variation ? Donner les valeurs affichées sur la calculatrice pour $a_8$ et $b_8$.



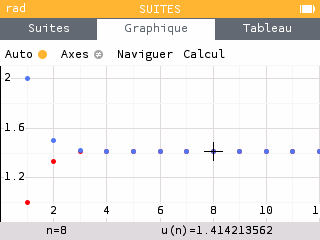
La suite $\left(a_n\right)$ semble croissante tandis que la suite $\left(b_n\right)$ semble décroissante. Les deux suites semblent converger vers un même nombre, d'ailleurs la calculatrice affiche la même valeur pour $a_8$ et $b_8$.

5. On admet que $0 < a_n < b_n$ pour tout entier naturel $n>0$.

   Démontrer les conjectures faites sur le sens de variation des deux suites.

$\displaystyle a_{n+1}-a_n = \frac{2}{b_{n+1}}-\frac{2}{b_n}=\frac{2\left(b_n-b_{n+1}\right)}{b_n b_{n+1}}$

Les termes de la suite $\left( b_n \right)$ étant strictement positifs, le sens de variation de la suite $\left(a_n\right)$ est l'inverse de celui de la suite $\left( b_n \right)$.

$\displaystyle b_{n+1}-b_n = \frac{a_n+b_n}{2}-b_n=\frac{a_n-b_n}{2}$

Or, on sait que $0 < a_n < b_n$ pour tout entier naturel $n>0$ donc la suite $\left( b_n \right)$ est décroissante et la suite $\left( a_n \right)$ est croissante pour tout entier naturel $n > 0$.

Vers la racine : convergence d'une suite numérique

On définit ainsi la suite $\left(u_n\right)$ pour tout entier naturel $n>0$ :

$\begin{cases} u_1=2 \\ \displaystyle u_{n+1}=\frac{1}{2}\left(u_n+\frac{2}{u_n}\right) \end{cases}$

1. A l'aide la calculatrice, conjecturer le sens de variation et la convergence de la suite.




2. On veut montrer que $u_n > \sqrt{2}$ pour tout $n > 0$.

   1. A l'aide du tableau de variation de la fonction $\displaystyle f\left(x\right)=\frac{1}{2}\left(x+\frac{2}{x}\right)$ définie sur $\left]0;+\infty\right[$, montrer que $f\left(x\right) > \sqrt{2}$ pour tout réel $x > \sqrt{2}$.

   On commence par déterminer la dérivée de la fonction : $\displaystyle f'\left(x\right)=\frac{1}{2}-\frac{1}{x^2}=\frac{x^2-2}{2x^2}$.

   $\begin{array}{|c|lcccr|} \hline x & 0 & & \sqrt{2} & & +\infty \\ \hline & +\infty & & & & +\infty \\ f\left(x\right) & & \searrow & & \nearrow & \\ & & & \sqrt{2} & & \\ \hline \end{array}$

   Sur l'intervalle $\left[ \sqrt{2} ; +\infty \right[$, la fonction est strictement croissante avec $f\left(\sqrt{2}\right)=\sqrt{2}$ donc si $x \geqslant \sqrt{2}$ alors $f \left( x \right) \geqslant \sqrt{2}$.

   2. En déduire par un raisonnement par récurrence que $u_n > \sqrt{2}$ pour tout $n > 0$.

   On cherche à démontrer la propriété : $u_n > \sqrt{2}$.

   On sait que $u_1=2$ donc la propriété est vérifiée au rang 1.

   Supposons que $u_n > \sqrt{2}$ ; on cherche maintenant à démontrer que $u_{n+1} > \sqrt{2}$.

   $u_{n+1}$ est défini tel que $u_{n+1} = f \left(u_n\right)$ avec $\displaystyle f\left(x\right)=\frac{1}{2}\left(x+\frac{2}{x}\right)$.

   Or, nous avons démontré précédemment que pour tout $x > \sqrt{2}$ alors $f\left(x\right) > \sqrt{2}$. Donc si $u_n \geqslant \sqrt{2}$, alors $f\left(u_n\right) \geqslant \sqrt{2}$, autrement dit $u_{n+1} \geqslant \sqrt{2}$. La propriété est vraie au rang $n+1$.

   La propriété est héréditaire. Or, elle est vraie au rang 1, donc elle est vraie pour tout entier naturel $n>0$.

3. Montrer que la suite $\left(u_n\right)$ est décroissante.

$\displaystyle u_{n+1}-u_n=\frac{1}{2}\left(u_n + \frac{2}{u_n}\right)-u_n= \frac{1}{u_n}-\frac{u_n}{2} = \frac{2-u_n^2}{2u_n}$

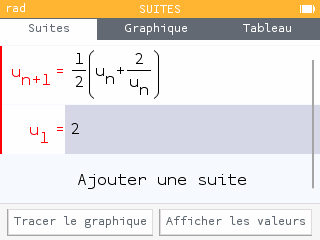
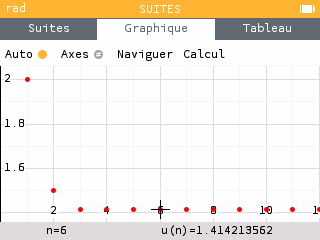
Or, on a montré que $u_n > \sqrt{2}$ pour tout $n > 0$ donc $u_{n+1}-u_n$ est négatif et la suite est décroissante.

4. Montrer que la suite converge vers un réel $l$.

La suite est décroissante et minorée : elle est donc convergente.

5. On admet que $l \left(l>0\right)$ vérifie $\displaystyle \frac{l^2+2}{2l}=l$. Déterminer $l$.

La résolution de l'équation nous donne $l=\sqrt{2}$.

Pour aller plus loin

La méthode d'Héron ne permet pas seulement de déterminer la valeur de la racine carrée de 2, mais aussi celle de la racine cubique de 2. Expliquer par quelle démarche procéder.