Approximation d'une intégrale avec Matplotlib

On s'intéresse à l'aire comprise entre la représentation graphique d'une fonction définie sur l'ensemble des réels par $\displaystyle f\left(x\right) = x^2$, l'axe des abscisses, et les droites d'équation $x=0$ et $x=1$.

On utilisera deux méthodes différentes de programmation, utilisant toutes les deux le module matplotlib.pyplot, afin d'obtenir une approximation de cette surface, calculée par $\displaystyle\int_0^1 x^2 \mathrm{d}x$.

Méthode de Monte-Carlo

Dans un premier temps, nous allons utiliser une méthode probabiliste afin d'obtenir une approximation de l'intégrale.

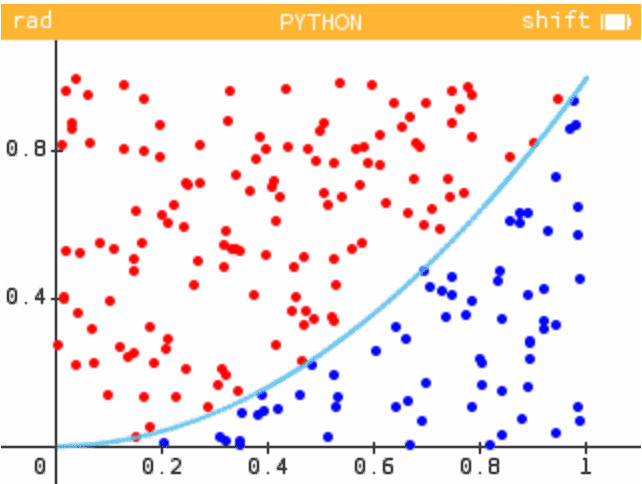
Nous allons générer aléatoirement un grand nombre de points dont les coordonnées sont telles que $0 \leq x \leq 1$ et $0 \leq y \leq 1$. Parmi ces points, certains se trouvent en-dessous de la courbe représentative de la fonction $f\left(x\right)=x^2$, d'autres au-dessus. Autrement dit, certains se trouvent dans l'intégrale, d'autres non.

1. En quoi connaître le rapport du nombre de points se trouvant dans la surface étudiée par rapport à la surface totale peut nous aider à calculer la valeur de cette intégrale (si le nombre de points générés est très grand) ?

Les coordonnées des points étant générées au hasard, la probabilité qu'un point se trouve dans l'intégrale est $\displaystyle\frac{\displaystyle A_{recherchée}}{A_{total}}$. Or, la surface totale qui est recouverte de points possède ici une aire égale à 1, donc la probabilité que le point se trouve dans l'intégrale est égale à l'intégrale elle-même.

Cela signifie que si l'on génère un très grand nombre de points, le rapport du nombre de points bleus par rapport au nombre de points total va tendre vers cette probabilité.

En effet, on peut modéliser la situation avec une variable aléatoire X qui prend la valeur 1 lorsque le point se trouve dans l'intégrale, 0 sinon. L'espérance de cette variable aléatoire, E(X), est égale à ce rapport. Or, pour un très grand nombre de points, l'espérance tend vers la probabilité définie précédemment. C'est la loi des grands nombres.

2. Quels sont les modules à importer au début du script ?

On importera les modules random et matplotlib.pyplot.

3. On propose dans un premier temps de définir $f(x)$ comme une fonction Python, puis de tracer dans un deuxième temps la courbe représentative correspondante dans une fonction graph().

   On rappelle que la fonction plot(X,Y) nécessite l'utilisation de deux listes. On pourra, par exemple, utiliser X=[i/100 for i in range(101)] pour définir X. Que permet cette ligne de code ?

Cette ligne permet de réaliser un découpage de l'axe des abscisses en 100 antécédents, depuis 0,00 jusqu'à 1,00. En effet, on ne peut générer que des entiers à l'aide de la boucle for. Cette astuce permet d'obtenir une liste de nombre décimaux, et cette liste sera suffisamment grande pour que le rendu paraisse curviligne.

4. Ecrire les deux fonctions f(x) et graph() et tester l'éxécution de cette dernière fonction.

def f(x):
  return x**2

def graph():
  X=[i/100 for i in range(101)]
  Y=[f(x) for x in X]
  plot(X,Y)
  show()
    

5. On propose maintenant de modifier légèrement ce programme en introduisant une variable n qui va correspondre au nombre de points générés.

   Nous allons créer une boucle au sein de laquelle deux variables x et y devront prendre des valeurs aléatoires. Quel test permettra de déterminer si le point se trouve dans l'intégrale étudiée ?

On va vérifier si $y \lt x^2$.

6. Si le test est réussi, le point prendra la couleur bleue, sinon il prendra la couleur rouge. On utilisera la fonction scatter(x,y,color="blue").

   Modifier la fonction graph() en conséquence puis tester.

def graph(n):
  X=[i/100 for i in range(101)]
  Y=[f(x) for x in X]
  plot(X,Y)
  for i in range(n):
    x=random()
    y=random()
    if y<f(x):
      scatter(x,y,color="blue")
    else:
      scatter(x,y,color="red")
  show()
    

7. On aimerait maintenant procéder au calcul de l'intégrale. Nous avons besoin de compter le nombre de points bleus à l'aide d'une autre variable. La fonction graph(n) devra ensuite renvoyer la valeur approximative de l'intégrale.

   Modifier la fonction en conséquence puis tester. Quelle approximation obtient-on pour $N=100$ ?

On ajoutera une variable inside avant la boucle, initialisée à zéro. Si le point est coloré en bleu, on incrémentera cette variable de 1.

Enfin, la dernière ligne de notre programme sera return inside/n.

Un script est disponible sur cette page.

8. Comment peut-on améliorer la précision de cette approximation ?

On améliore la précision en augmentant le nombre de points générés sur le graphique.

Méthode des rectangles

Nous allons maintenant réaliser un programme permettant de calculer approximativement notre intégrale en découpant la surface étudiée en rectangles.

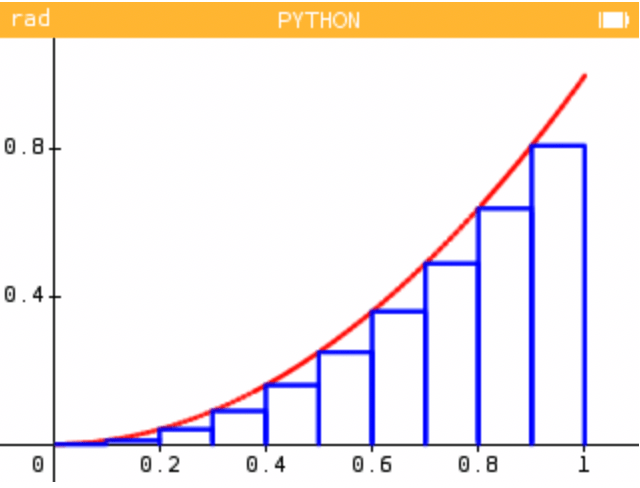
On pourra réutiliser la même fonction f(x) et le début de la fonction graph(n) précédente afin de tracer la courbe représentative de la fonction carré. Il ne nous restera plus qu'à tracer les rectangles.

1. Dans ce programme, on veut que la variable n désigne le nombre de rectangles qui découperont la surface. On déclare une variable delta qui correspondra à la largeur d'un rectangle.

   Exprimer delta en fonction de n.

La largeur totale de la surface est égale à 1, d'où delta=1/n.

2. Nous allons créer une boucle au sein de laquelle figureront deux listes : la liste rect_x contiendra les abscisses des quatre points correspondants au rectangle à tracer, et la liste rect_y contiendra les ordonnées correspondantes. La fonction plot() permettra ensuite de relier les points. Chaque itération de la boucle correspond ainsi à un rectangle.

   Plusieurs méthodes sont possibles. On propose ici d'utiliser une variable x que l'on incrémentera progressivement.

   On considère un rectangle quelconque se trouvant dans la surface étudiée.

   

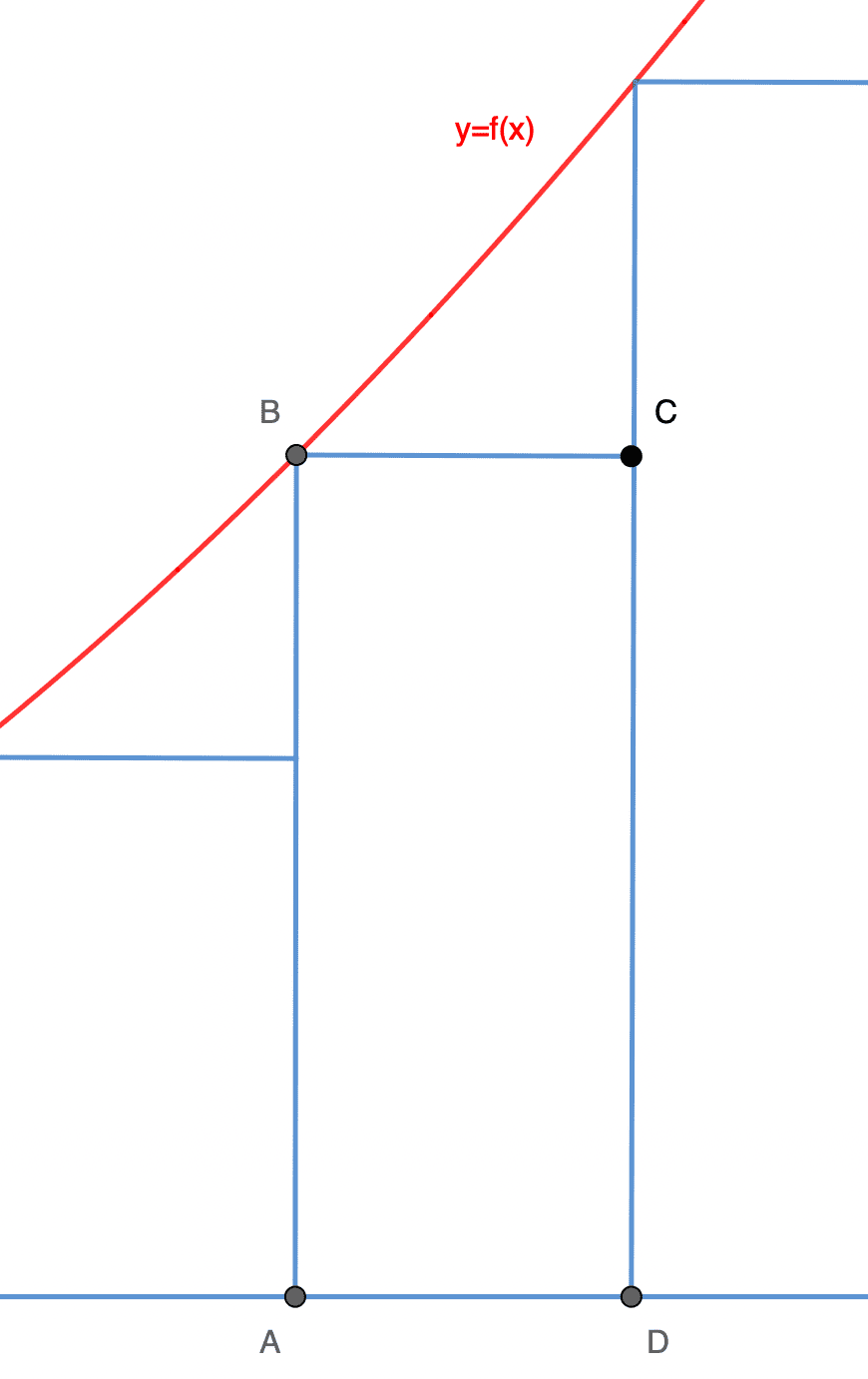
   On note $x$ l'abscisse du point A. On rappelle que l'on note $\delta$ la largeur d'un rectangle. Déterminer en fonction de $x$ et $\delta$ les coordonnées des points A, B, C et D.

On obtient : $A(x;0)$, $B(x;f(x))$, $C(x+\delta;f(x))$ et $D(x+\delta;0)$.

3. Quelle est la valeur initiale de la variable x ? Et de combien l'incrémenter à la fin d'une boucle ?

La variable doit être initialisée à zéro. A la fin d'une boucle, on aura x+=delta.

4. A l'aide des questions précédentes, compléter la fonction graph(n) et tester le programme avec graph(10).

def graph(n):
  X=[i/100 for i in range (101)]
  Y=[f(i) for i in X]
  plot(X,Y,color="red")
  delta=1/n
  x=0
  for k in range(n):
    rect_x=[x,x,x+delta,x+delta]
    rect_y=[0,f(x),f(x),0]
    plot(rect_x,rect_y,color="blue")
    x+=delta
  show()
    

5. On veut maintenant procéder au calcul de l'intégrale. On propose d'utiliser une variable somme qui stocke la somme des aires des rectangles dessinés et, à chaque itération de la boucle, ajoute l'aire du rectangle correspondant.

   Modifier le programme en conséquence et l'éxécuter pour graph(20).

Avant la boucle, on initialise somme à 0. A la fin de la boucle (mais avant d'incrémenter x !), somme est incrémentée de $f(x) \times \delta$. Enfin, on ajoute return somme en dernière ligne.

Un script est disponible sur cette page.

6. Comment peut-on améliorer la précision obtenue ?

Pour améliorer la précision du résultat, il faut découper la surface en davantage de rectangles.

On peut aussi modifier l'algorithme afin qu'il calcule l'aire, non plus de rectangles mais de trapèzes.

7. Comparer brièvement les deux méthodes.
Avec la méthode des rectangles, la valeur obtenue en éxécutant le programme deux fois de suite avec un $n$ identique est la même, contrairement à la méthode de Monte-Carlo pour laquelle on obtiendra un résultat différent à chaque fois, même en générant le même nombre de points. La seconde méthode est déterministe, alors que la première est probabiliste.