Calcul de la masse de Jupiter

Fonctions trigonométriques Outils de régression Transdisciplinaire

Objectif

L'objectif de cette activité est d'utiliser les outils de régression de la calculatrice afin de calculer la masse de Jupiter à partir du mouvement de quatre de ses satellites grâce à la 3e loi de Kepler.

Contexte

Johannes Kepler est un astronome allemand du XVIIe siècle. A l'aide des extraordinaires observations de son mentor Tycho Brahe, il modélise trois lois mathématiques susceptibles d'expliquer le mouvement des planètes autour du Soleil.

La première loi stipule que la trajectoire des planètes forme une ellipse dont le Soleil est l'un des foyers. La seconde loi stipule que, tout au long de de leur trajet, les planètes balaient par rapport au Soleil une aire identique en un intervalle de temps égal. Cela implique que les planètes accélèrent très légèrement lorsqu'elles se trouvent plus proches du Soleil. La troisième loi, enfin, évoque une relation entre la masse du Soleil et le ballet des planètes qui gravitent autour.

C'est cette 3e loi qui va nous permettre de calculer la masse de la géante Jupiter !

Pour cette activité, on proposera au choix : d'utiliser le logiciel CLEA: The Revolution of the Moons of Jupiter du Project CLEA, très simple d'utilisation ; ou d'utiliser la feuille de données en dernière page du PDF.

Quelques rappels avant de commencer

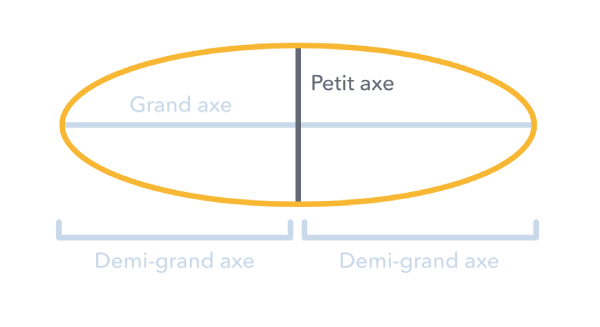
On appelle grand axe le plus grand diamètre de l'ellipse.

On se placera dans un référentiel dans lequel le centre de Jupiter est immobile et constitue l'origine du repère.
On appelle période T le temps nécessaire à un satellite pour faire un tour complet autour de Jupiter.
On appelle demi-grand axe la moitié du plus grand diamètre de la trajectoire de Jupiter.

Acquérir des données à l'aide de JupLab

Notre objectif est tout d'abord d'utiliser le logiciel JupLab afin de calculer, par l'observation, la période et la valeur du demi-grand axe des satellites de Jupiter.

Le logiciel JupLab permet de réaliser des observations des positions des quatre principaux satellites de Jupiter (Io, Callisto, Ganymède et Europe) à une date donnée. Nous allons nous intéresser au déplacement, au fil du temps, du satellite sur l'axe des abscisses par rapport au point zéro que constitue le centre de la planète. Ainsi, une position à gauche de Jupiter correspondra à une abscisse négative et une position à droite, une abscisse positive. Le logiciel donne justement la valeur absolue de cette abscisse (l'unité est le diamètre de Jupiter) lorsque l'on clique sur la lune concernée. Une petite précision est apportée, W pour west/E pour east, que nous traduirons donc en signe positif ou négatif comme expliqué précédemment. On relèvera donc, à partir d'un temps $t=0$ et au fil des jours, le déplacement des satellites.

Préparer au brouillon une feuille de données. La première colonne correspond au temps (en heures) écoulé depuis la première observation. Les autres correspondront, pour chaque satellite, à la distance apparente (en diamètre jovien) entre le satellite et la planète.
Générer à l'aide du logiciel une première position des astres en entrant une date quelconque qui correspondra à $t=0$ . Cliquer sur chacun des satellites pour connaître sa distance à Jupiter et reporter la valeur dans la colonne correspondante. On notera une abscisse négative si le satellite est à l'ouest (W), positive si le satellite est à l'est (E).
Cliquer sur Next pour obtenir les positions suivantes 24 heures plus tard et répéter la démarche. Attention à bien noter la date et l'heure pour pouvoir calculer le temps écoulé depuis $t=0$ .

On incitera les élèves à réaliser des relevés variés : 1 à 2 relevés par jour sur une petite période, 1 relevé tous les 4 à 5 jours sur une autre. En effet, la période de Callisto est d'environ 17 jours, alors que celle d'Io est inférieure à 2 jours.

Pour plus d'explications sur le fonctionnement du logiciel : consulter le site de l'Observatoire de Paris-Meudon

Pour la petite histoire !

Le logiciel permet de mieux comprendre les observations que Galilée a pu faire à l'aide de sa lunette astronomique en 1610. Observant Jupiter, il observe un alignement de points lumineux autour de celle-ci. Parfois trois, parfois quatre. Parfois tous sont alignés du même côté de Jupiter, parfois ils sont dispersés de part et d'autre. Sans connaître la vraie nature de ces objets, il finit par comprendre qu'ils tournent autour de Jupiter et s'il ne les voit pas tous certaines nuits, c'est parce qu'ils sont cachés derrière la planète ! C'est grâce à cette observation qu'il comprend que la Terre ne constitue pas le seul centre de rotation de l'Univers, comme on le pensait à l'époque. C'est un argument de plus en défaveur du géocentrisme !
Les satellites de Jupiter doivent leur nom aux conquêtes de Zeus : Europe est une princesse enlevée par Zeus qui avait pris la forme d'un taureau ; Callisto et Io sont deux jeunes filles transformées, l'une en ourse, l'autre en génisse, suite à la jalousie d'Héra ; Ganymède est l'échanson des dieux et amant de Zeus.

Déterminer les caractéristiques de la trajectoire des satellites

On cherche maintenant à déterminer la période et le demi-grand axe de chacun des satellites, à l'aide de l'application Régressions de la calculatrice.

Dans l'onglet Données, entrer en X1 les données relatives au temps (en heures) et en Y1 les données relatives à la position du premier satellite.
Dans l'onglet Graphique, presser ok puis sélectionner Trigonométrique.
Déterminer graphiquement la période et le grand axe en déplaçant le curseur sur la courbe. On rappelle que la période correspond à l'intervalle de temps mesuré entre deux crêtes (mais pour plus de précision, on peut mesurer plusieurs périodes et diviser par leur nombre). Le grand axe correspond à la distance mesurée entre la plus haute et la plus basse valeur. On n'oubliera pas de diviser cette distance par deux pour obtenir le demi-grand axe.
Répéter pour chacun des quatre satellites.

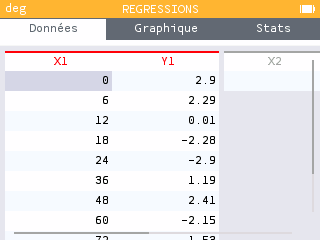
Dans l'outil Régressions, on entre en X1 les données relatives au temps, et en Y1 les données relatives à la position.

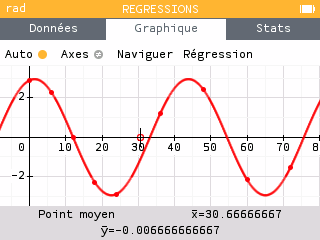
On utilise une régression trigonométrique.

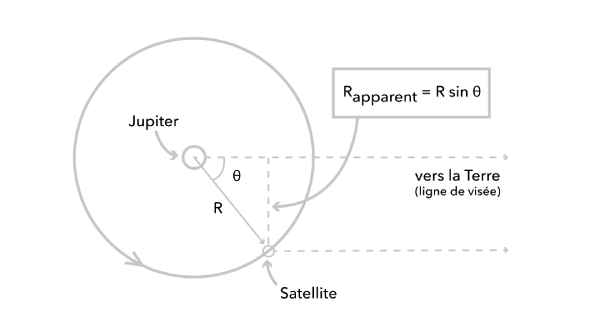
L'évolution du rayon apparent suit une fonction sinusoïdale.

On pourra expliquer aux élèves pourquoi la distance du satellite par rapport au centre de Jupiter forme une sinusoïdale en faisant le lien avec le cercle trigonométrique. On rappelle que la trajectoire du satellite est quasi-circulaire.

On trouve une période d'approximativement 43h pour Io, 84h pour Europe, 173h pour Ganymède et 401h pour Callisto. Concernant le demi grand-axe, on trouve environ 3 diamètres joviens pour Io, 4,7 D.J pour Europe, 7,5 D.J pour Ganymède et 13,7 D.J pour Callisto.

Calculer la masse de Jupiter

La troisième loi de Kepler stipule qu'il existe une relation mathématique entre le carré de la période de révolution d'un astre et le cube de son demi grand-axe.

Dans l'application Régressions de la calculatrice, entrer en abscisse le carré de la période (en heures) et en ordonnées le cube du demi grand axe (en diamètre jovien). Puis, dans l'onglet Graphique, sélectionner une régression proportionnelle.
Le coefficient de proportionnalité est lié à la masse de Jupiter, cependant il nous faut les bonnes unités afin de déterminer celle-ci.

En effet, d'après la 3e loi de Kepler :

$\displaystyle \frac{a^3}{T^2}=\frac{GM}{4\pi^2}$

Ici, $M$ correspond à la masse de Jupiter, $T$ est la période des satellites et $a$ leur demi grand-axe.
1. Proposer une expression de $M$ à partir de la relation précédente.
2. On appelle constante gravitationnelle la valeur $G = 6,67 \times 10^{-11} \, m^{3}.kg^{-1}.s^{-2}$ . En déduire les conversions à réaliser sur le terme $\displaystyle \frac{a^{3}}{T^{2}}$ , coefficient directeur de la droite obtenue par régression linéaire.
3. Le diamètre de Jupiter est d'environ 140 000 km. En déduire la masse de Jupiter

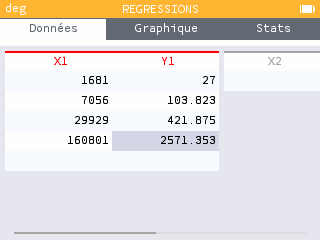
On entre en X1 les carrés des périodes et en Y1 les cubes des demi-grands axes.

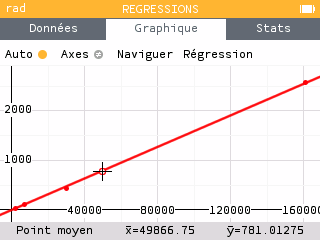
On utilise une régression linéaire pour vérifier la relation de proportionnalité.

On constate qu'il existe bel et bien une relation de proportionnalité entre le carré de la période et le cube du demi-grand axe. La valeur du coefficient de proportionnalité est accessible dans un sous-menu avec ok une fois que la courbe de régression est tracée. On trouve aussi la valeur du r2 dans ce sous-menu, qui nous donne une indication supplémentaire sur la fiabilité du modèle.

La 3e loi de Kepler nous donne :

$\displaystyle M = \frac{a^{3}}{T^{2}} \times \frac{4\pi^{2}}{G}$

On a $\displaystyle \frac{a^{3}}{T^{2}}$ qui est le coefficient directeur donné par la régression, qu'il faudra donc convertir dans les bonnes unités : $a$ en mètres et $T$ en secondes. D'où une masse de Jupiter égale à $2,0 \times 10^{27}$ kg.