Ice Cream

Modeling Optimization Pythagorean theorem Right triangle trigonometry

Objective

The objective of this activity is to optimize the distance between ice cream shops to determine the best location for the ice cream production center using geometry, the Pythagorean theorem, and trigonometry.

Planning

A new ice cream company, I Scream, You Scream Ice Cream, plans to purchase three buildings in a city to house their first three ice cream shops. The buildings are located at points A(0, 2), B(0, -2) and C(5, 0). A production center will also be constructed to provide the ice cream to the shops. The owner, Heath, wants to build the production center in a location that would allow his three delivery trucks to travel as little as possible to help minimize costs.

Images of ice cream

Let the site of the production center be located at a point S. Assume that it is possible to drive directly from the production center to each ice cream shop. Also assume that each ice cream shop sells the same amount of ice cream. Determine the best location for Heath to place the production center.

The following hints can be provided to students:

Draw a picture!
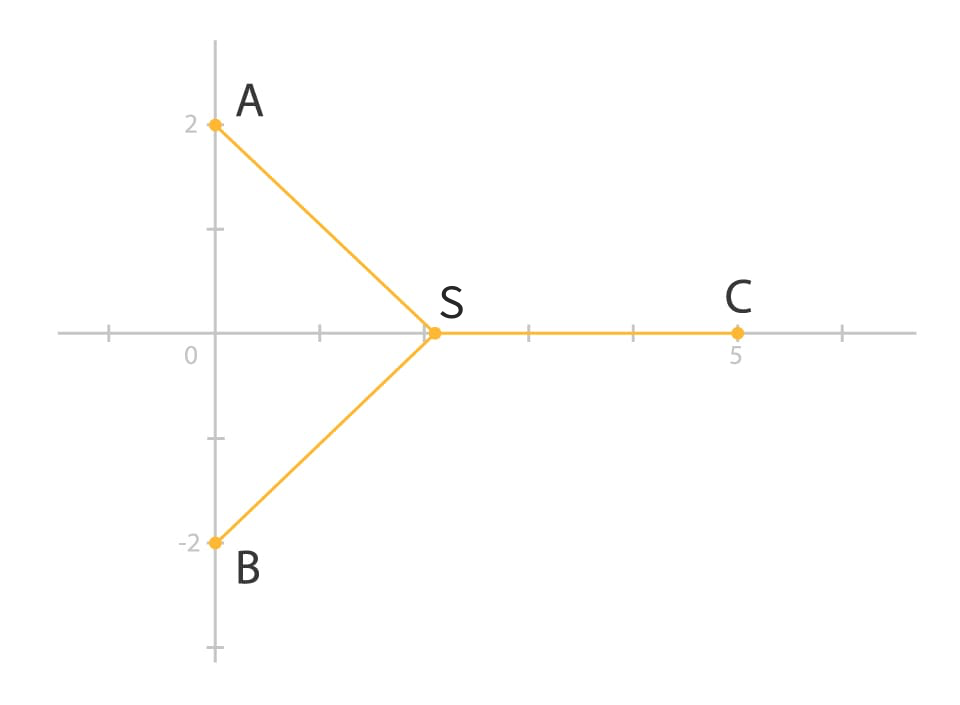
Remember, we want to find the point S for which $SA + SB + SC$ is smallest.
Let $x$ represent the length of $OS$ .

If $y$ represents $SA + SB + SC$ , write $y$ in terms of $x$ .

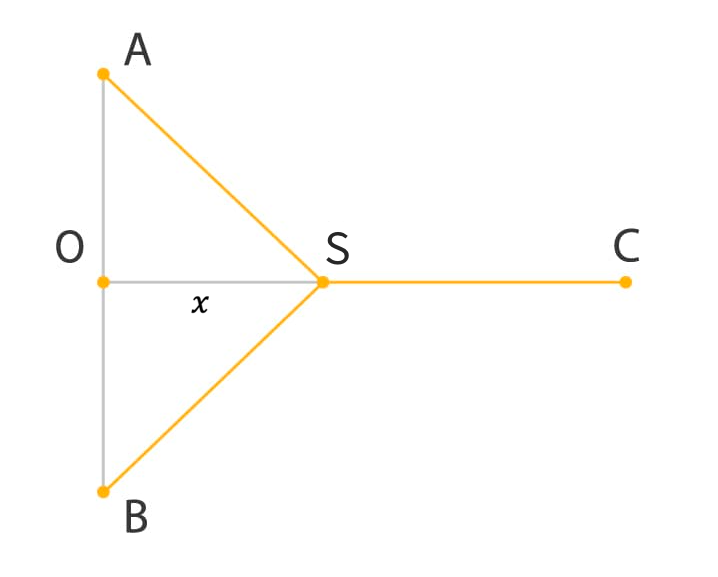
The following is a potential solution method. For additional approaches, see the solutions at the end of the page.

Let $x$ represent the length of $OS$ and $y = SA + SB + SC$ .

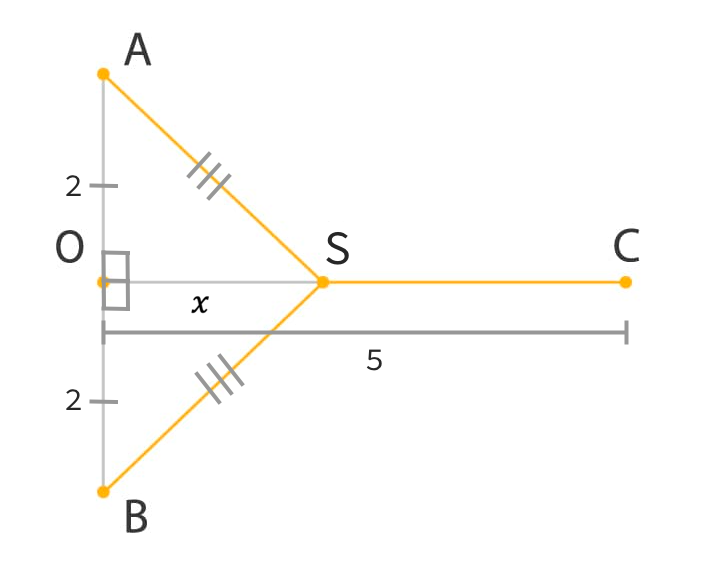
Using Pythagorean Theorem, we can determine the length of $AS$ in terms of $x$ :

$x^2+2^2=(AS)^2$

$x^2+4=(AS)^2$

$AS = \sqrt{x^2+4}$

Similarly, $BS = \sqrt{x^2+4}$ .

To determine the length of $SC$

$OC = OS + SC$

$5 = x + SC$

$SC = 5 - x$

Thus we have

$y = \sqrt{x^2+4} + \sqrt{x^2+4} + (5-x)$

$y = 2\sqrt{x^2+4} + 5 - x$

Using the equation above, students may graph the function $y = 2\sqrt{x^2+4} + 5 - x$ and look for a minimum.

Using the Grapher app, enter the relation $y = 2\sqrt{x^2+4} + 5 - x$ .

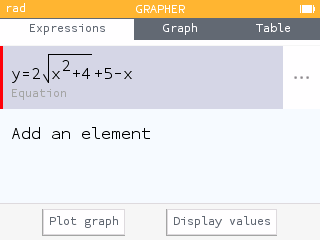
Graphing the relation, we see the minimum occurs at the point $\left( 1.155,8.464 \right)$ .

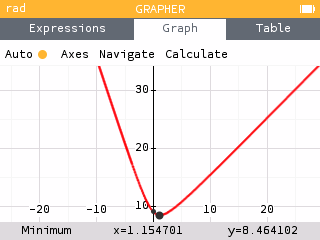
That is, when the production center is placed 1.155 units east of shops A and B and horizontal with shop C, the distance traveled by the three delivery trucks is minimized to 8.464 units.

Relocation

While planning the construction of his new ice cream shops, Heath found out that the locations of shops A and B would not work due to zoning issues. Fortunately, he was able to find new locations for his shops. He now plans to place shop A at (0,3) and shop B at (0,-3). Shop C is still planned for (0,5). Where should Heath build his production center considering these new locations?

Similar to the original prompt, let $x$ represent the length of $OS$ and $y = SA + SB + SC$ .

Using Pythagorean Theorem, we can determine the length of $AS$ in terms of $x$ :

$x^2+3^2=(AS)^2$

$x^2+9=(AS)^2$

$AS = \sqrt{x^2+9}$

Similarly, $BS = \sqrt{x^2+9}$ .

We still have $SC = 5 - x$ .

Thus we have

$y = 2\sqrt{x^2+9} + 5 - x$

Using the Grapher app, students can find the minimum of $y = 2\sqrt{x^2+9} + 5 - x$ .

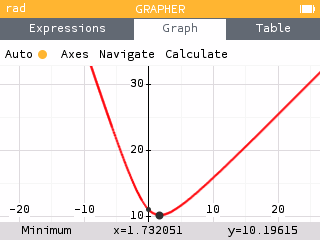
We see the minimum occurs at the point $\left( 1.732,10.196 \right)$ .

That is, based on the new locations of shops A and B, the production center should be placed 1.732 units east of shops A and B and horizontal with shop C to minimize the distance traveled by the three delivery trucks to 10.196 units.

Expansion

After great success in ice cream sales, Heath decides it is time to expand his business by relocating shops A and B into larger buildings. The new locations of shops A and B are (0,4) and (0,-4), respectively. Shop C will stay at (0,5). Because gas is one of his highest expenses, Heath is also willing to relocate his production center to minimizes the distance traveled by his delivery trucks. Where should the production center be located?

We can again, let $x$ represent the length of $OS$ and $y = SA + SB + SC$ .

Using Pythagorean Theorem, we can determine the length of $AS$ in terms of $x$ :

$x^2+4^2=(AS)^2$

$x^2+16=(AS)^2$

$AS = \sqrt{x^2+16}$

Similarly, $BS = \sqrt{x^2+16}$ .

We still have $SC = 5 - x$ .

Thus we have

$y = 2\sqrt{x^2+16} + 5 - x$

Using the Grapher app, students can find the minimum of $y = 2\sqrt{x^2+16} + 5 - x$ .

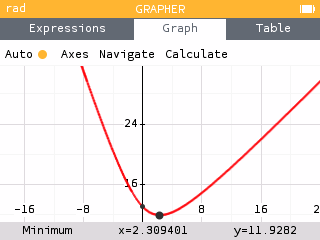
We see the minimum occurs at the point $\left( 2.309,11.928 \right)$ .

That is, based on the new locations of shops A and B, the production center should be placed 2.309 units east of shops A and B and horizontal with shop C to minimize the distance traveled by the three delivery to 11.928 units.

Noticing Patterns

Based on your findings from the previous problems, if Heath wanted to move shop A and B even further away, what do you think would happen to the location of his ice cream production center?

In each of the previous problems, the distance between shops A and B was getting larger and larger. With each increase, the x-value of the minimum also increased. That is, the production center moved further and further east, closer to shop C.

A Fixed Production Center

Assume that shop C is at (5,0) and the production center has already been built at S(3,0). If Heath still wants to build shops A and B equal distance from the origin and on the y-axis, where would each shop need to be located to minimize the distance traveled by his delivery trucks?

We can use the data from our previous problems to model the relationship between the location of shop A and the location of the production center. We can then use this model to predict where shop A should be located given the location of the production center.

Using the Regression application, we enter the y-values for shop A from our previous three problems into X1 and the resulting x-values of the production center into Y1.

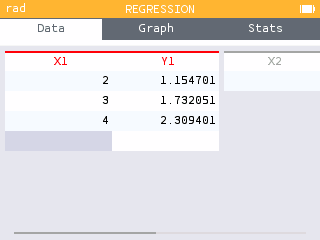
On the Graph tab, we construct a scatterplot and add a linear regression model.

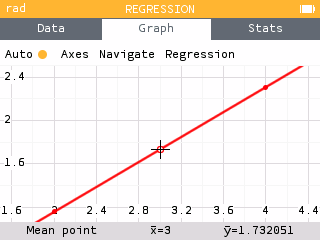
Using the prediction tools, we can find X given a predicted Y. That is, we can find the y-value of shop A given the predicted x-value of the production center, 3.

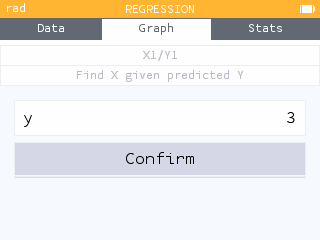
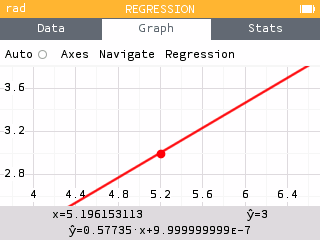
We see that in order for the production center to be located at (3,0), shop A would need to be located at (0, 5.196). Thus shop B would need to be located at (0, -5.196).

We can verify this answer by finding where the production center should be built to minimize the distance traveled by the delivery trucks assuming shop A is built at (0, 5.196) and shop B is built at (0, -5.196) like we did in the first three problems.

Let $x$ represent the length of $OS$ and $y = SA + SB + SC$ .

Using Pythagorean Theorem, we can determine the length of $AS$ in terms of $x$ :

$x^2+5.196^2=(AS)^2$

$x^2+26.998=(AS)^2$

$AS = \sqrt{x^2+26.998}$

Similarly, $BS = \sqrt{x^2+26.998}$ .

We still have $SC = 5 - x$ .

Thus we have

$y = 2\sqrt{x^2+26.998} + 5 - x$

Using the Grapher app, students can find the minimum of $y = 2\sqrt{x^2+26.998} + 5 - x$ .

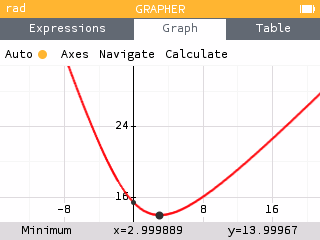
We see the minimum occurs at the point $\left( 3,14 \right)$ .

The x-value of the minimum, 3, verifies that when shop A is located at (0, 5.196) and the production center is located at (0,3), the distance traveled is minimized.

Additional solution approaches

Approach 1

Let $x$ represent the length of $SC$ and $y = SA + SB + SC$ .

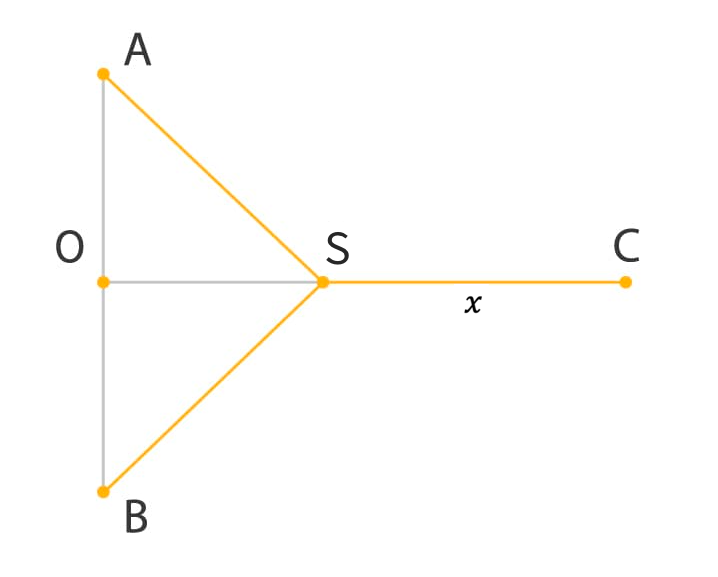
Sketch of three ice cream shops and production center

Using Pythagorean Theorem, we can determine the length of $AS$ in terms of $x$ :

$(5-x)^2+2^2=(AS)^2$

$(5-x)^2+4=(AS)^2$

$AS = \sqrt{(5-x)^2+4}$

Similarly, $BS = \sqrt{(5-x)^2+4}$ .

Thus we have

$y = \sqrt{(5-x)^2+4} + \sqrt{(5-x)^2+4} + x$

$y = 2\sqrt{(5-x)^2+4} + x$

Using the equation above, students may graph the function $y = 2\sqrt{(5-x)^2+4} + x$ and look for a minimum.

Using the Grapher app, we see the minimum occurs at the point $\left( 3.845,8.464 \right)$ .

To determine the location of point S, we subtract the x-value from 5 and recieve 1.155.

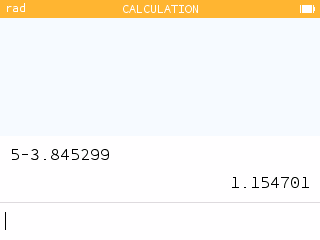
That is, when the production center is placed 1.155 units east of shops A and B and horizontal with shop C, the distance traveled by the three delivery trucks is minimized to 8.464 units.

Approach 2

Let $x$ represent the length of $AS$ and $y = SA + SB + SC$ .

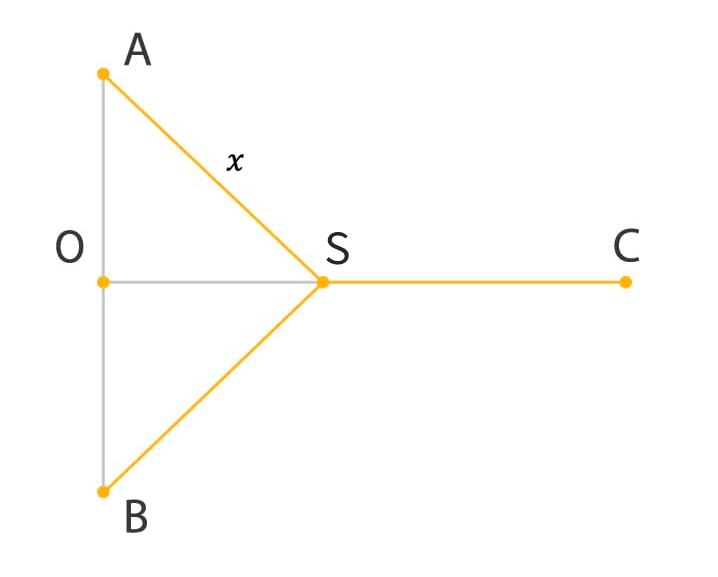
Because right triangle AOS and right triangle BOS are congruent, $x = BS$ .

Using Pythagorean Theorem, we can determine the length of $OS$ in terms of $x$ and then find the length of $SC$ :

$(OS)^2+2^2=x^2$

$(OS)^2+4=x^2$

$OS = \sqrt{x^2-4}$

To determine the length of $SC$

$OC = OS + SC$

$5 = \sqrt{x^2-4} + SC$

$SC = 5 - \sqrt{x^2-4}$

Thus we have

$y = x + x + 5 - \sqrt{x^2-4}$

$y = 2x + 5 - \sqrt{x^2-4}$

Using the Grapher app, students can find the minimum of $y = 2x + 5 - \sqrt{x^2-4}$ .

We see the minimum occurs at the point $\left( 2.309,8.464 \right)$ .

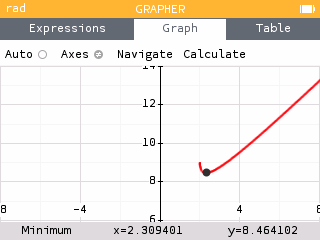
To determine the location of point S, we use Pythagorean Theorem to set up the equation

$OS^2 + 2^2 = 2.309^2$

Using the Solver app, we can solve the equation and find $OS = 1.155$ .

That is, when the production center is placed 1.155 units east of shops A and B and horizontal with shop C, the distance traveled by the three delivery trucks is minimized to 8.464 units.

Approach 3

Students may also set up the problem so that $x$ represents one of the unknown angles within the triangle and use trigonometry to solve. To demonstrate one approach:

Let $x$ represent $m\angle ASO$ and $y = SA + SB + SC$ .

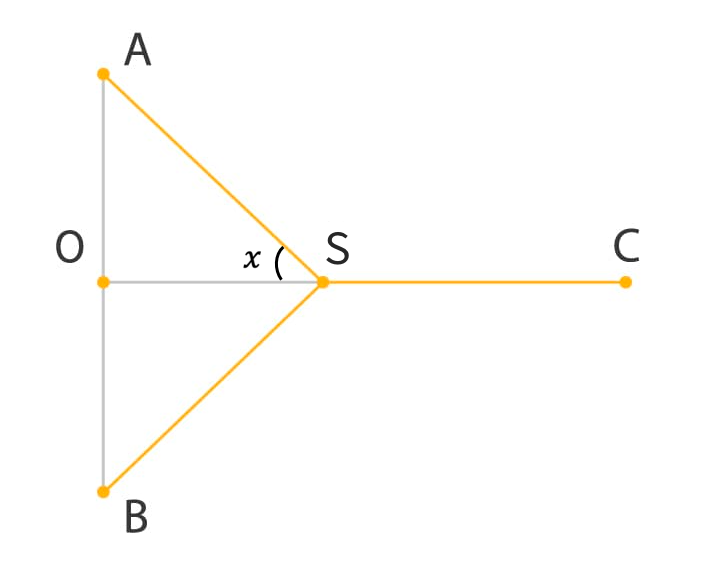
Using right triangle trigonometry, we have:

$\sin \left( x \right) = \frac{2}{AS}$

$AS \sin \left( x \right) =2$

$AS = \frac{2}{\sin \left( x \right)}$

Similarly, $BS = \frac{2}{\sin \left( x \right)}$

Also,

$\tan \left( x \right) = \frac{2}{OS}$

$OS = \frac{2}{\tan \left( x \right) }$

To determine the length of $SC$ ,

$OC = OS + SC$

$5 = \frac{2}{\tan \left( x \right) } + SC$

$SC = 5 - \frac{2}{\tan \left( x \right) }$

Thus we have

$y = \frac{2}{\sin \left( x \right)} + \frac{2}{\sin \left( x \right)} + 5 - \frac{2}{\tan \left( x \right) }$

$y = 2\frac{2}{\sin \left( x \right)} + 5 - \frac{2}{\tan \left( x \right) }$

$y = \frac{4}{\sin \left( x \right)} + 5 - \frac{2}{\tan \left( x \right) }$

Using the Grapher app, students can find the minimum of $y = \frac{4}{\sin \left( x \right)} + 5 - \frac{2}{\tan \left( x \right) }$ .

We see the minimum occurs at the point $\left( 60,8.464 \right)$ .

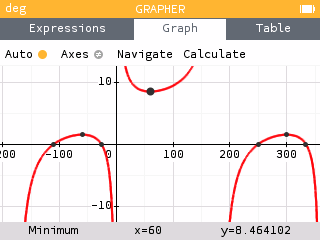
To determine the location of point S, we evaluate $OS = \frac{2}{\tan \left( x \right) }$ for $x = 60$ .

We find that $OS = 1.155$ . That is, when the production center is placed 1.155 units east of shops A and B and horizontal with shop C, the distance traveled by the three delivery trucks is minimized to 8.464 units.