Wire Problem - A Calculus Approach
Optimization Area First Derivative Test Modeling
Objective
The objective of this activity is to optimize the area formed when a wire of a given length is cut and used to create two shapes.
A wire that is 40 cm long will be used to form a circle, a square, or both. The wire can be cut so that one section is used to create a circle and the other section is used to create a square.
How should the wire be used to form shapes with a maximum combined area? How much of the wire should be used to create the circle? How much should be used to create the square?
There are many ways that students may approach this problem. Consider selecting and sequencing techniques when having students present their work. In calculus, using the First Derivative Test is ideal.
Overall, this problem consists of selecting where to cut the wire, constructing a square from one piece and a circle from the other, and computing the area of each shape.
Let be the distance from the left end of the wire as shown below.

Cutting here will result in two pieces of wire, one with length and the other with length . Let the piece of wire with length be used to construct the circle and the piece of wire with length be used to construct the square.
For the circle, the length of the wire corresponds to the circumference of the circle. That is, . To determine the area of the circle, we must first solve for
Now we find the area of the circle using
For the square, the length of the wire corresponds to its perimeter. That is, . To calculate the area of the square, we must first determine the side length of the square. Since a square has 4 congruent sides, we have:
Now we find the area of the square using
The total combined area can be found by adding the two areas
Creating a Table
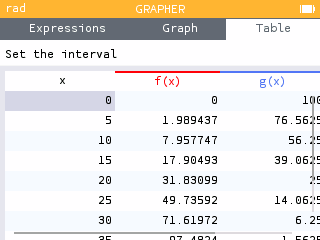
Using the area formula above, students may consider a guess-and-check method by trying out different values . A table of values for and its corresponding areas can be constructed.
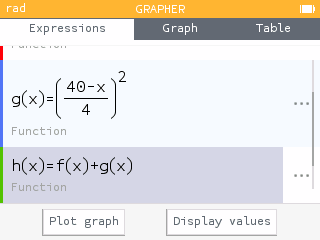
Using the Grapher app, input functions to compute the area of the circle, the area of the square, and the total area. Then view the Table tab and input possible values for .

| x | Area of Circle | Area of Square | Total Area |
|---|---|---|---|
| 0 | 0 | 100 | 100 |
| 5 | 1.989 | 76.563 | 78.552 |
| 10 | 7.958 | 56.25 | 64.208 |
| 15 | 17.905 | 39.063 | 56.967 |
| 20 | 31.831 | 25 | 56.831 |
| 25 | 49.736 | 14.063 | 63.794 |
| 30 | 71.62 | 6.25 | 77.87 |
| 35 | 97.482 | 1.563 | 99.045 |
| 40 | 127.324 | 0 | 127.324 |
Using this approach, students will find the maximum at . That is, when the entire piece of wire is used to construct a circle, the area is maximized at .
Graphing
Using the area formula above, students may graph the function and look for maximums.
Using the Grapher app, enter the function .

Before viewing the Graph, open the Function options by clicking on the three dots to the right of the expression. Adjust the plot restriction in the Function options to match the practical domain for this scenario.
Graphing the function, we see the maximum occurs at the right endpoint .
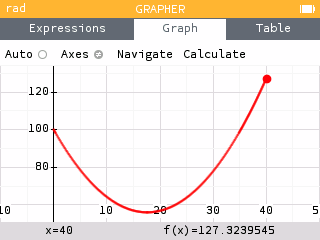
That is, when the entire piece of wire is used to construct a circle, the area is maximized at
First Derivative Test
Using the area formula above, students may use the first derivative test to determine the extrema of the function . The Extreme Value Theorem states that since is continuous on , then must have a maximum on the interval. This problem demonstrates the importance of checking the endpoints of the interval.
Using the Grapher app, enter the function .

Before viewing the Graph of the derivative, open the Function options by clicking on the three dots to the right of the expression. Adjust the plot restriction in the Function options to match the practical domain for this scenario.

Graphing the first derivative, we see a zero occurs at . Therefore, our only critical point is at . However, since the derivative is negative before and positive after , this critical point corresponds to a minimum.
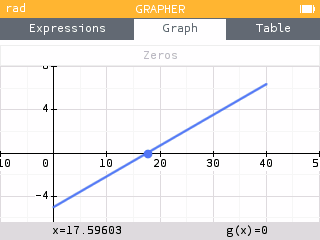
At this point, we should check the endpoints. Using the Calculation app, we can evaluate the function at the endpoints.

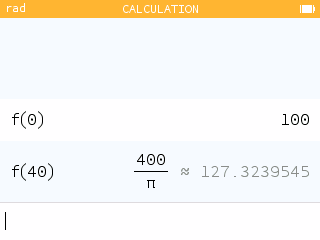
We see that the right endpoint outputs the largest value. That is, when the entire piece of wire is used to construct a circle, the area is maximized at .
Additional Prompts
The following alterations can be used depending on your learning objectives:
- Change the length of the wire for each student or group of students.
- Replace the length of the wire with a parameter .
- Instruct students to find the minimum combined area instead of the maximum area.
- Use the wire to form a circle and an equilateral triangle with minimized combined area.
- Use the wire to form a square and an equilateral triangle with a minimized combined area.
- Use the wire to form a circle and another regular polygon with a minimized combined area.