Fair Games
Probability Distribution Discrete Random Variable Expected Value Probability
Objective
The objective of this activity is to compute probabilities using probability distributions of discrete random variables and to calculate and interpret the mean (expected value) and standard deviation of discrete random variables.
State Fairs are one of the most well known fall events with their funnel cakes, exhilarating rides, music events, and games! Fair games often entice guests with their promise of oversized stuffed animals, hats, jerseys, and other exciting prizes. However, not all fair games are actually "fair"!
Many games of chance are designed so that the game attendant has a better chance of winning that the players. Every now and then, the players will win, which gives them confidence to carry on playing! However, if the game is weighted towards the game attendant, then they will always win in the long run!
A fair game is a game in which there is an equal chance of winning or losing. We can say that a game is fair if the probability of winning is equal to the probability of losing.
Balloon Pop
Consider a game where balloons are attached to a board and the player throws a dart in hopes of popping a balloon.
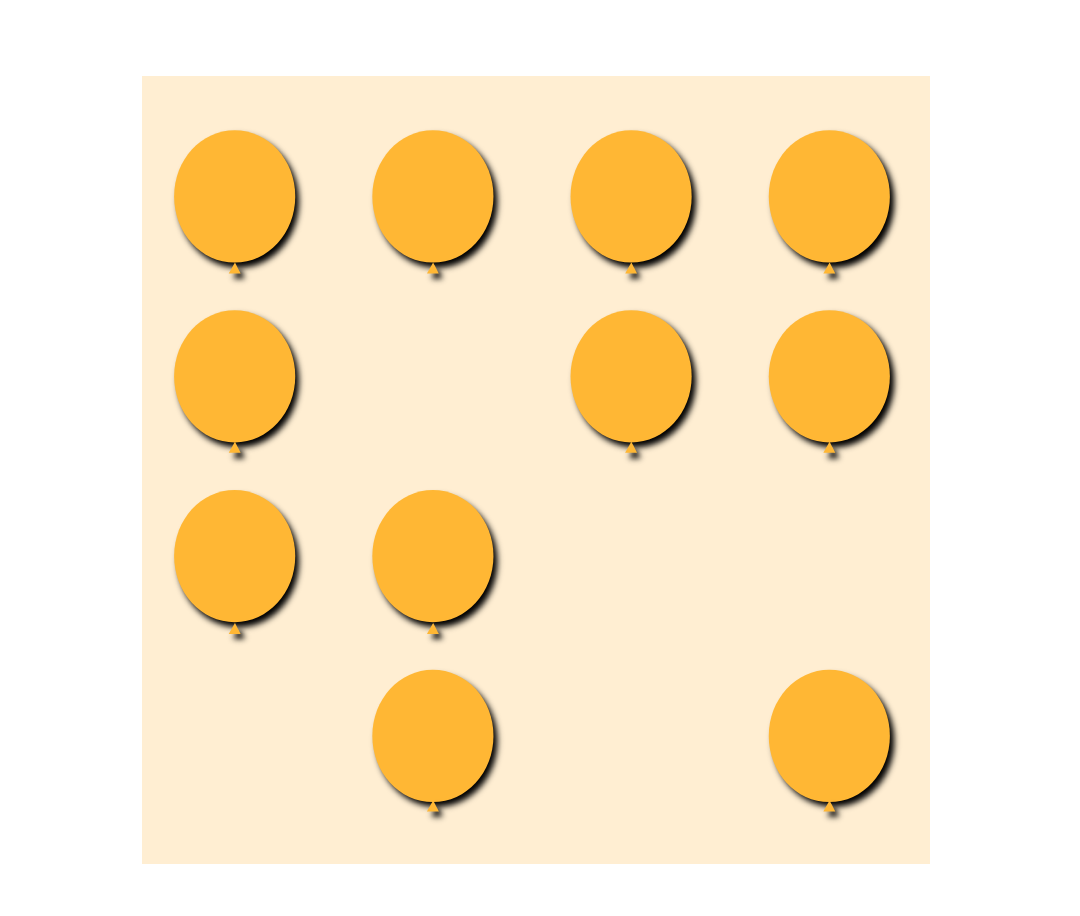
- If the dimensions of the board are 3.5 feet wide and 3.5 feet high, and the diameter of each balloon is 8 inches, what is the probability that a randomly thrown dart hits a balloon?
- Assume it costs $1 to play the game and that if the player hits a balloon, they win $3. Is this a fair game? If not, who has the advantage?
- Does winning $4 for hitting the balloon change who has the advantage?
- How much should the winner receive after paying $1 to play so that the game is fair?
To determine the probability of hitting a balloon, we compute .

The probability of hitting a balloon with a randomly thrown dart is 0.313
A game is "fair" if the expected value is 0. If a player hits a balloon, their net gain is $2. If they do not hit a balloon, they lose $1.

The expected value is -$0.06. That is, in the long run, the player is expected to lose an average of $0.06 each game in many, many games. This is not a fair game as it gives the game attendant an advantage.

Yes! By winning $4 for hitting a balloon, the player's net gain is $3 and the expected value is now $0.25. The player has the advantage and is expected to win an average of $0.25 each game in many, many games.
A game is "fair" if the expected value is 0. To determine the winning payout in a fair game, we need to solve

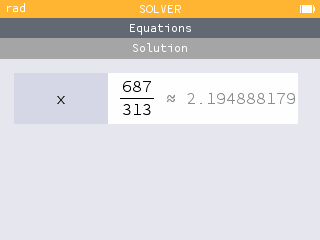
For the game to be "fair", the winner should receive $3.19 so that their net gain is $2.19.
A Probability Distribution
The game attendant wants to make things more exciting! They decide to add different colored balloons and vary the prize money depending on which balloon you hit!
To account for the added expenses, the game now costs $2 to play. If a player hits the gray balloon, they win $4. Hitting a yellow balloon wins $5. And if the player hits the one white balloon, they win $10!
Let's define the random variable net gain from a single game.
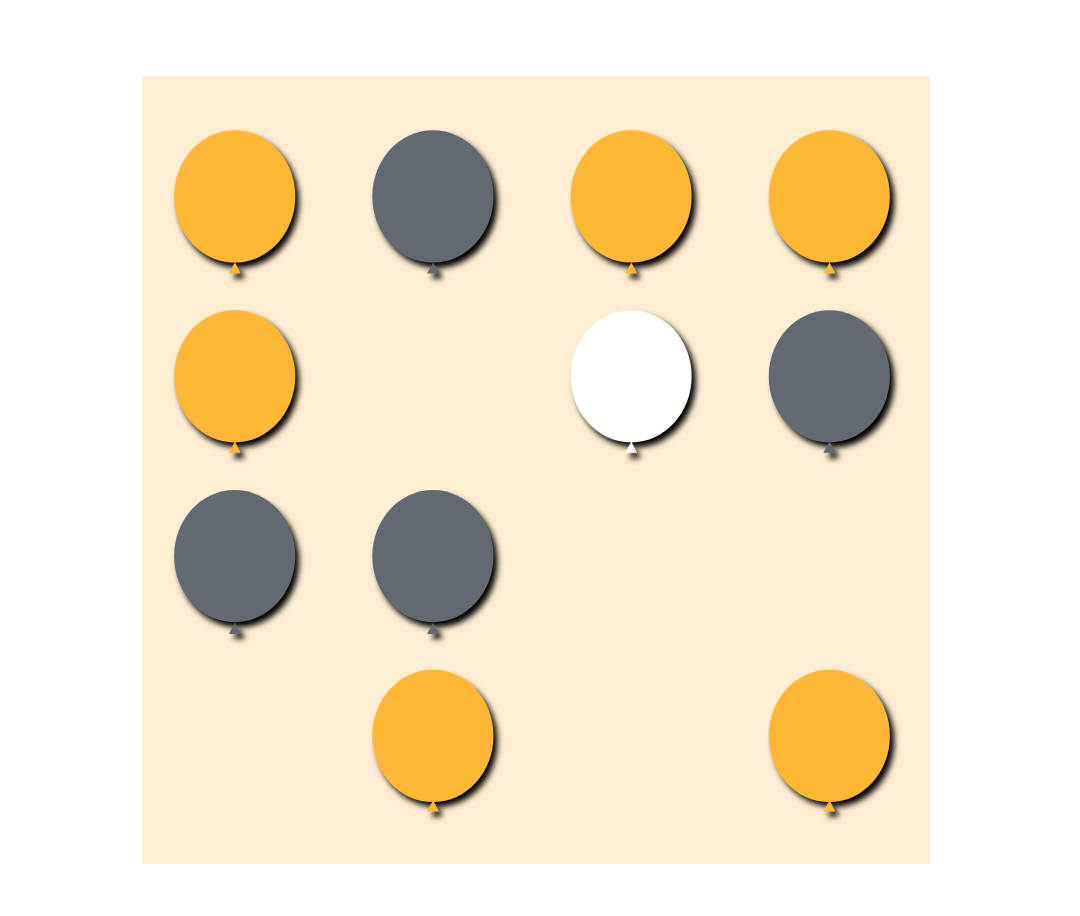
- Find the probability distribution of .
- Determine and interpret the result.
- Compute the expected value of . Explain what this result means for the player.
- Compute and interpret the standard deviation of the random variable .
- Determine a set of prize winnings after paying $2 to play so that the game is fair.
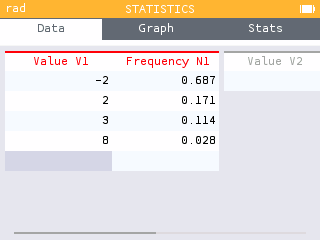
To determine the probability of hitting each color of balloon, we compute .

| Net gain | -2 | 2 | 3 | 8 |
|---|---|---|---|---|
| Probability | 0.687 | 0.171 | 0.114 | 0.028 |
. The probability that the player's net gain after one game is $3 or more is 0.142
Using the Statistics app, input the values in V1 and the corresponding values in N1.
The expected value, mean, is found in the Stats tab.
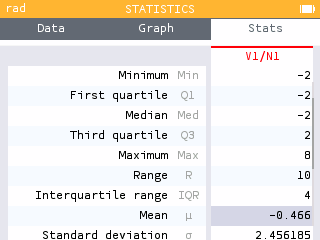
In the long run, the player is expected to lose an average of $0.47 each game in many, many games. Although the prize money is higher than the original game, the player is more disadvantaged!
The standard deviation of , , is also found in the Stats tab.
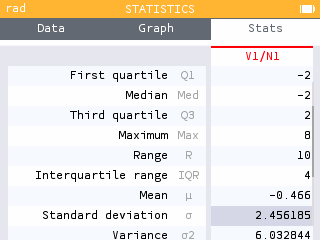
In a random game, the player's net game will typically differ from -$0.47 by about $2.46.
Answers will vary. One method to find a set of "fair" prize winnings is to keep all prizes the same except for one. For example, we can keep all prizes the same except the white balloon and solve the equation
Using the Equations app, we find the solution
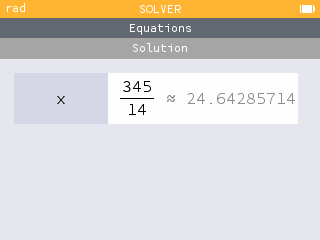
The $2 game will be "fair" if players recieve $4 for hitting a yellow balloon, $5 for hitting a gray balloon and $26.64 for hitting the white balloon.
Ring Toss
The stand next to the balloon game offers another game involving tossing rings on pegs. Let's define the random variable net gain from a single game of ring toss.
The probability distribution of is shown below.
| Net gain | -3 | 2 | 5 | 11 | 25 |
|---|---|---|---|---|---|
| Probability | 0.55 | 0.25 | 0.17 | 0.02 | 0.01 |
- Compute the expected value and standard deviation of . Explain what this result means for the player.
- Assume a guest plays both the updated Balloon Pop game and the Ring Toss game and that the outcomes of the games are independent. Let net gain from both games. That is, let . Compute the expected value and standard deviation of . Explain what this result means for the player.
Using the Statistics app, input the values in V1 and the corresponding values in N1.
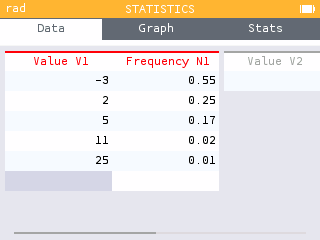
The expected value and standard deviation are found in the Stats tab.
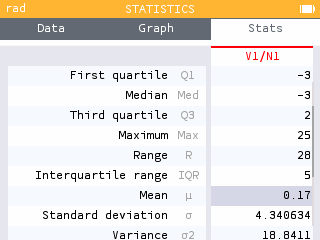
In the long run, the player is expected to win an average of $0.17 each game in many, many games. On a random game, the net gain will typically vary from $0.17 by about $4.34. The player has an advantage in the Ring Toss game!
The expected value when playing both games is
.
Because the outcome of the games are independent, that standard deviation is

A player will lose an average of $0.13 each time in the long run. On a random pair of games, a player will typically differ from this net gain by about $4.99