
Émilie Feral — 5 mars 2020
Malloc - Chronique d'une mort certaine
La gestion de la mémoire est un point critique dans un système embarqué. Cet article explique les raisons qui nous ont conduits à nous passer de malloc, la méthode standard d’allocation dynamique en C.
Allocation dynamique : quel besoin dans Epsilon ?
Lorsque l’on tape un calcul, celui-ci est analysé puis stocké sous forme d’arbre.
Ainsi 1+2*π est stocké sous la forme :
Évidemment ces arbres sont de taille variable, en fonction de l’expression entrée. On a donc besoin d’un espace mémoire dans lequel on peut stocker des objets dont la taille n’est pas connue en avance. Communément, un espace de mémoire appelé la heap (tas en français) sert d’espace de stockage pour tous les objets dont la taille n’est connue qu’à l’exécution.
En C, la fonction malloc de la librairie standard permet de réserver une zone mémoire d’une taille donnée à l’exécution : c’est l’allocation dynamique. Jusqu’à la version 1.7 d’Epsilon, c’est ainsi qu’étaient stockées les expressions mathématiques dans la calculatrice : chaque noeud de l’arbre était alloué quelque part sur la heap et gardait des pointeurs vers ses enfants.
Dans l’exemple ci-dessous le noeud + conservait ainsi deux adresses indiquant où étaient stockés ses enfants 1 et x.
Pourquoi changer de stratégie ?
Cependant, cette méthode connaît certaines limites :
- La fragmentation de la mémoire : l’espace mémoire de la heap peut ne plus contenir suffisamment d’espace mémoire consécutif pour un nouveau noeud alors qu’elle possède encore assez de zone vide (non consécutive) pour stocker l’objet.
L'allocation de l'espace orange échoue alors qu'il resterait assez de mémoire disponible si elle n'était pas fragmentée…
- De plus, l’algorithme de
malloca été pensé pour réussir à allouer une zone mémoire dans un maximum de cas possibles toutes utilisations confondues. En utilisant cette fonction générique, on ne tire pas partie de certaines spécificités des expressions qu’on y alloue, par exemple :- Une taille de zone allouée caractéristique ; bornée entre le plus petit noeud et le plus gros noeud qu’on utilise.
- Deux noeuds alloués consécutivement sont susceptibles d’être utilisés et détruits en même temps (s’ils appartiennent au même arbre par exemple).
Par ailleurs, l’utilisation de la heap oblige une certaine rigueur de la part du développeur :
- Dès qu’un objet est alloué sur la heap, il faut considérer la possibilité que l’allocation mémoire puisse échouer. Ceci oblige le développeur à gérer ce cas manuellement à travers tout le code.
- Il faut éviter la fuite mémoire : lorsque l’on oublie d’effacer un objet alloué sur la ‘heap’, à chaque exécution de ce bout de code, on va remplir un peu plus la heap sans jamais la nettoyer. Le software finira inévitablement par planter (ou aboutir continuellement à des erreurs dues au manque de mémoire) lorsque la heap sera pleine.
Comment stocker les expressions sans malloc ?
Pour toutes ces raisons, lors de la mise à jour 1.8 d’Epsilon, nous avons décidé de ne plus utiliser malloc. Il fallait choisir une nouvelle méthode pour stocker les expressions qui
s’ajusterait mieux aux exigences de notre module mathématique.
On a réservé une zone mémoire de 32 ko utilisée comme mémoire tampon pour stocker les expressions : c’est notre Pool. Pour éviter la mémoire fragmentée, les arbres d’expressions y sont stockés consécutivement. De plus, si un noeud possède des enfants, ceux-ci sont les arbres qui le suivent directement dans le Pool. Ceci évite entre autre d’avoir à conserver des pointeurs vers ses enfants dans un noeud.
Certains types de noeuds ont une taille variable en fonction de leurs données : par exemple, un noeud représentant un nombre entier sera d’autant plus grand qu’il possède de chiffres en base 2^32.
Comme le pool ne possède aucune zone de mémoire vide entre deux noeuds, l’adresse où est stockée un noeud ‘glisse’ lorsque qu’un noeud précédent est supprimé. Pour désigner un noeud on ne peut donc plus utiliser de pointeur. C’est pourquoi nous attribuons à chacun un identifiant unique décidé arbitrairement.
Pool contenant 1+2π
Un nouveau modèle qui présente d’autres limites
En pratique, pour accéder à un noeud à partir de cet identifiant, il faut parcourir le pool jusqu’à trouver le noeud avec cet identifiant. Par ailleurs, la modification d’une expression translate la mémoire de tout le Pool à partir du noeud modifié. Les processus de lecture et d’écriture sont par conséquent plus lents que lorsque l’on utilisait malloc (ils sont linéaires avec la taille du Pool alors qu’ils étaient en temps constant). Comme souvent en informatique, c’est un compromis entre un gain en temps et un gain en espace mémoire.
Toutefois, pour éviter une régression importante en temps de calculs, notre Pool est associé à un cache qui mémoïse l’association entre un noeud et son adresse mémoire. Ce cache est mis à jour à chaque fois qu’un noeud est modifié.
| id | adresses |
|---|---|
| + | 0x0232 |
| 1 | 0x023d |
| × | 0x023f |
| 2 | 0x0242 |
| π | 0x0247 |
| cos | 0x024a |
| + | 0x084d |
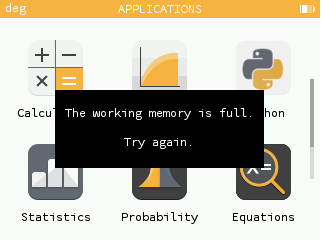
Finalement, la mise à jour 1.8 a permis d’optimiser l’utilisation de la mémoire et d’en profiter pour gérer le cas où trop d’expressions ont été allouées.
Lien vers les fichiers implémentant le Pool d’expressions:
- La classe des noeuds stockés dans le Pool : tree_node.h et tree_node.cpp.
- La classe des identifiants associés aux noeuds : tree_handle.h et tree_handle.cpp
- La classe du Pool : tree_pool.h et tree_pool.cpp.

Émilie Feral — Développeuse
Émilie est diplômée de l'École Polytechnique et elle a rejoint NumWorks en juillet 2016 comme développeuse. Si votre calculatrice peut réaliser les calculs les plus fous ou tracer une courbe à une vitesse inégalée : c'est grâce au travail d'Émilie ! Émilie fait des merveilles en C++ mais c'est aussi la championne de l'équipe sur de nombreux terrains : basket, vélo et même cirque !

