Approximation de e par la méthode d'Euler
Dérivation Fonction exponentielle Suites numériques Programmation Python
Objectif
L'objectif de cette activité est d'amener à la construction de la courbe représentative de la fonction exponentielle par la méthode d'Euler et d'obtenir une approximation de e grâce à l'écriture d'un algorithme Python.
A la découverte de la fonction exponentielle
On cherche à construire point par point une fonction avec deux caractéristiques précises : et .
-
Rappeler la définition du nombre dérivé au point d'abscisse et en déduire une approximation du nombre pour un réel positif et proche de 0.
-
On choisit . Remplir le tableau suivant :
x 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1 On propose ensuite de tracer la courbe correspondant aux données ci-dessus grâce à un algorithme Python utilisant le module
matplotlib.pyplot.On pourra utiliser la fonction
plot(listeX,listeY)du modulematplotlib.pyplotqui relie les points dont les coordonnées sont contenues dans deux listes : listeX et listeY. -
D'après le tableau ci-dessus, exprimer les évolutions de et en utilisant les suites numériques.
-
En déduire une expression (approximative) de avec entier naturel.
-
On pose maintenant . Exprimer et en déduire une expression de .
-
On appelle le nombre , appelé exponentielle, lorsque tend vers l'infini. Plus est grand et plus le résultat tend vers la valeur recherchée.
On propose de programmer un algorithme en Python permettant de calculer ce nombre pour plusieurs valeurs de à l'aide d'une fonction
calcul(n).
Pour un positif et proche de 0 :
| x | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| 1 | 1,1 | 1,21 | 1,331 | 1,464 | 1,611 | 1,772 | 1,949 | 2,144 | 2,358 | 2,594 |

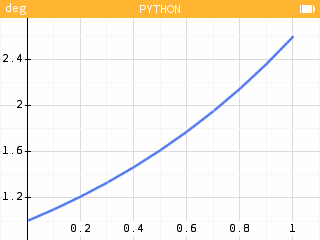
On peut proposer aux élèves plus avancés de construire la fonction sur un intervalle [0;5], par exemple, et de la comparer à la courbe exponentielle. Voir le script sur cette page.
On remarque que les antécédents suivent une suite arithmétique de raison 0,1 et de premier terme 0. Les images, quant à elles, suivent une suite arithmétique de raison 1,1 et de premier terme 1.
