Autour de la suite de Syracuse
Suites numériques Programmation Python
Objectif
Programmation Python pour étudier les curiosités des suites de Syracuse
On appelle une suite de Syracuse une suite construite sur un schéma très simple :
-
On choisit un entier .
-
S'il est pair, on le divise par deux.
-
S'il est impair, on le multiplie par 3 et on lui soustrait 1.
-
Et on recommence le procédé…
Coder les suites de Syracuse
On cherche à réaliser une fonction syracuse(m,n) qui va lister les premiers éléments de la liste de Syracuse démarrant du nombre .
On propose d'utiliser une variable liste dans laquelle on stockera les valeurs successives de la suite.
-
Comment initialiser la variable
listeen début de programme ? -
Quel type de boucle permet de lister les premiers éléments d'une liste ?
-
Quelle instruction permet d'ajouter un élément à la liste ?
-
A l'aide des questions précédentes, écrire la fonction
syracuse(m,n)et tester avecsyracuse(15,10).On suggère d'utiliser
int(m/2)pour limiter l'affichage des décimales au sein de la liste. -
On propose de réaliser une fonction
syracuse_graph(m)qui permet de représenter graphiquement les 100 premiers termes de la suite de Syracuse du nombre .On pourra définir une liste
X=[i for i in range(100)]en abscisse et utiliser le programme précédent pour obtenir la liste des éléments de la suite à entrer en ordonnées. L'instructiongraph(X,Y)permettra la représentation graphique.On n'oubliera pas, bien sûr, d'importer le module
matplotlib.pyplot!
En début de programme, on connaît déjà le premier élément de la liste : c'est le nombre de départ. On utilisera liste=[m]
On connaît le nombre d'éléments à lister, on utilisera donc l'instruction for i in range(n-1).
Attention, on connaît déjà le premier terme de la liste, il faut donc calculer les autres.
On écrira liste.append(m).
def syracuse(m,n):
liste=[m]
for i in range(n-1):
if m%2==0:
m=m/2
else:
m=3*m+1
liste.append(m)
return liste
def syracuse_graph(m):
X=[i for i in range(100)]
Y=syracuse(m,100)
plot(X,Y)
show()
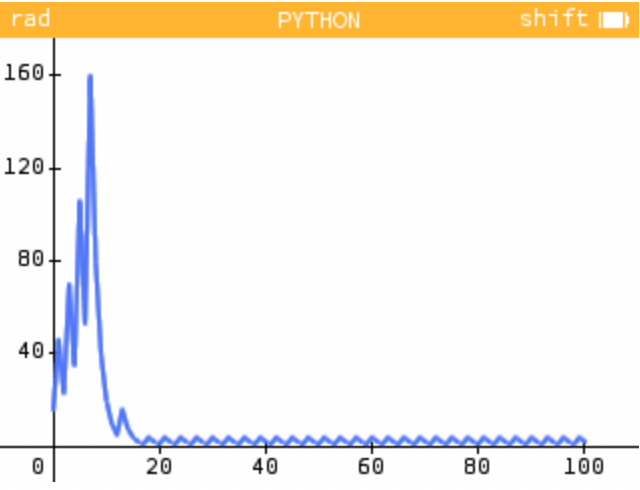
Toutes les suites de Syracuse mènent à Rome
Il existe une hypothèse mathématique qui n'a encore jamais été démontrée... mais jamais infirmée non plus : toutes les suites de Syracuse atteignent le nombre 1, à un moment ou à un autre. C'est la conjecture de Syracuse.
-
Reprenons la suite de Syracuse du nombre 15 et, à l'aide de notre fonction, affichons non plus les 10 mais les 20 premiers termes de la suite. Atteignez-vous le nombre 1 ?
-
Essayez avec d'autres nombres, d'autres valeurs. Affichez par exemple les premiers termes de la suite de Syracuse de 31 : combien de termes devez-vous afficher à l'écran avant de trouver le nombre 1 ?
-
Nous allons créer une fonction
syracuse_search(m)qui, s'appuyant sur la conjecture précédente, permet de connaître l'indice du premier élément de la liste égal à 1. Notre programme doit donc boucler jusqu'à ce que le nouvel élément calculé soit égal à 1.Quel type de boucle utiliser ici ?
-
Ecrire la fonction
syracuse_search(m)et vérifier que son exécution est cohérente avec vos essais précédents. -
Testez votre programme avec d'autres valeurs. Existe-t-il une corrélation entre le nombre et l'indice obtenu par la fonction
syracuse_search(m)? -
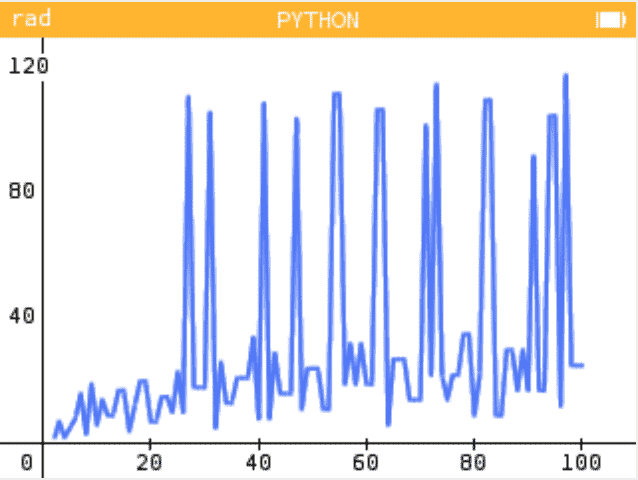
Pour vérifier notre réponse, on propose de rédiger une fonction
graph()qui permet de représenter graphiquement les indices obtenus par la fonction précédente pour les nombres allant de 2 à 100.On créera une première liste X avec les entiers allant de 2 jusqu'à 100, puis une seconde Y dans laquelle on stockera les résultats de
syracuse_searchpour ces nombres respectifs.
On atteint bien le nombre 1 !
Il faut aller au-delà de 100 nombres dans la liste pour trouver le nombre 1 dans la suite de Syracuse de 31. Il faut précisément 107 éléments dans la liste pour y arriver.
On peut discuter de l'évolution de la suite une fois qu'elle a atteint la valeur 1. Les nombres suivants sont forcément 4, 2, puis 1 et se répètent à l'infini.
On utilisera une boucle while. Si l'on conserve le même procédé, la condition à respecter dans la boucle est m!=1.
On créera donc une variable pour comptabiliser le nombre de boucles. Si l'on souhaite que cette variable compte le nombre d'éléments dans la liste, on l'initialise à 1. Si l'on souhaite que la variable compte l'indice de l'élément dans la suite, l'élément initial étant d'indice 0, alors on l'initialise à 0.
def syracuse_search(m):
i=0
while m!=1:
if m%2==0:
m=int(m/2)
else:
m=3*m+1
i+=1
return i
Dans la suite de Syracuse de 31, le premier nombre 1 est obtenu avec l'indice 106. Dans la suite de Syracuse de 15, il est obtenu avec l'indice 17.
A priori, non ! On constate que syracuse_search(31) renvoit 106 alors que syracuse_search(30) renvoie 18 et syracuse_search(32) renvoie 5.
def graph():
X=[i for i in range(2,101)]
Y=[syracuse_search(i) for i in X]
plot(X,Y)
show()
Effectivement, il ne semble pas y avoir de corrélation entre l'indice du premier élément 1 et le nombre . Il ne semble pas non plus y avoir de périodicité.