Le problème des lunules

On attribue la formulation de ce problème à Hippocrate de Chios, qui vécut au Ve siècle avant notre ère.

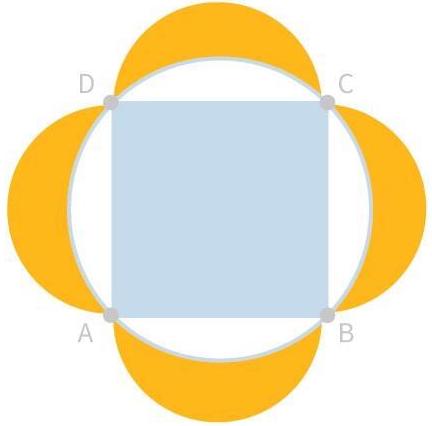
On considère un carré de côté $c$ que l'on inscrit dans un cercle, de rayon $r$. On construit ensuite quatre lunules à partir des côtés du carré, c'est-à-dire que l'on construit les demi-cercles de diamètre AB, BC, CD et AD et on s'intéresse à la surface de ces demi-cercles auxquels on soustrait la surface contenue dans le cercle de rayon $r$. Les lunules apparaîssent en jaune sur la figure.

Nous allons montrer que l'aire de ces quatre lunules est identique à l'aire du carré ABCD.

1. Exprimer la relation existant entre $c$ et $r$.

$c=r\sqrt{2}$

2. On s'intéresse à la lunule construite sur le côté AB. Exprimer en fonction de $r$, puis en fonction de $c$, la surface comprise entre le segment [AB] et l'arc de cercle $\overset{\displaystyle\frown}{AB}$.

On appelle O le centre du cercle et du carré ABCD.

La surface comprise dans le quart de cercle auquel appartient l'arc de cercle $\overset{\displaystyle\frown}{AB}$ est égale à $\displaystyle\frac{\pi r^2}{4}$. On y soustrait la surface du triangle OAB, soit $\displaystyle \frac{r^2}{2}$. D'où une surface à égale à $\displaystyle \left(\pi-2\right)\frac{r^2}{4} = \left(\pi-2\right)\frac{c^2}{8}$.

3. En déduire la surface de la lunule.

On soustrait le résultat obtenu à la question précédente à l'aire du demi-cercle de diamètre AB. L'aire du demi-cercle de diamètre AB est égale à $\displaystyle \frac{1}{2}\pi\left(\frac{c}{2}\right)^2$, d'où :

$\displaystyle \mathscr{A}_{lun}=\frac{\pi c^2}{8} - \left(\pi-2\right)\frac{c^2}{8} = \frac{c^2}{4}$

4. En conclure que la surface des 4 lunules est égale à la surface du carré ABCD.

D'après le résultat précédent, la somme des surfaces des lunules est égale à $c^2$, ce qui est bien l'aire du carré ABCD.