Approximation de Pi

Trigonométrie Programmation Python

Objectif

Calcul de Pi par approximation à l'aide de polygones réguliers et réalisation d'un algorithme de seuil.

Cette méthode s'inpire de celle d'Archimède, à l'origine du premier algorithme de calcul pour déterminer la valeur de $\pi$ . Nous allons cependant nous faciliter la tâche en utilisant la trigonométrie… que ne connaissait pas Archimède !

D'abord un carré…

Un carré est inscrit dans un cercle, lui-même inscrit dans un autre carré.

On considère un cercle de rayon 1 dans lequel est inscrit un carré. Ce cercle est lui-même inscrit dans un autre carré.

On fait maintenant l'hypothèse que le périmètre du cercle est compris entre celui des deux carrés.

Exprimer le périmètre de ces deux carrés et en déduire un encadrement de $\pi$ .

On commence par s'intéresser au carré intérieur. On sait que le cercle admet pour rayon 1. Cela signifie que les diagonales du carré sont égales à 2 et on en déduit le côté d'un carré :

$2 c^{2} = 2^{2} \iff c = \sqrt{2}$

D'où $P_{int}=4\sqrt{2}$ .

On s'intéresse ensuite au carré extérieur : il s'agit d'un carré de côté 2, d'où $P_{ext}=8$ .

Le périmètre du cercle est encadré par les périmètres des deux carrés, donc :

$P_{int} < 2\pi < P_{ext} \iff 2\sqrt{2} < \pi < 4$

… puis un hexagone…

On reprend le même type de raisonnement mais en remplaçant maintenant les carrés par des hexagones réguliers.

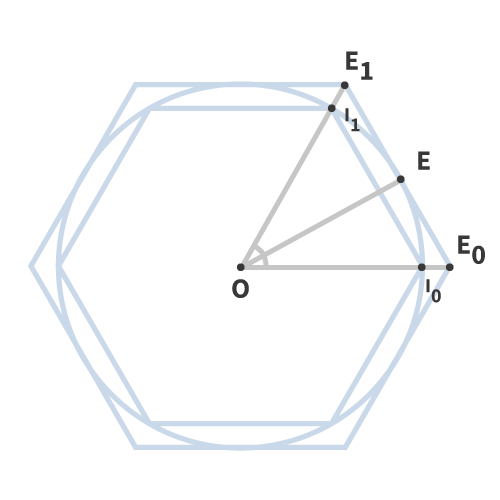
Un hexagone est inscrit dans un cercle, lui-même inscrit dans un autre hexagone.

On s'intéresse à l'angle formé en O par les points $O$ , $I_{0}$ et $I_{1}$ . Que peut-on dire sur cet angle ? En déduire la nature du triangle $OI_{0}I_{1}$ , puis un périmètre de l'hexagone intérieur.

L'angle au centre de l'hexagone est égal à $\displaystyle \frac{2\pi}{6} = \frac{\pi}{3}$ . Le triangle est donc équilatéral et $P_{int}=6$ .

Quelle est la nature du triangle $OEE_{0}$ ? En déduire une expression du segment $\left[EE_{0}\right]$ à l'aide des relations trigonométriques, puis du périmètre de l'hexagone extérieur.

OE est une hauteur des triangles $OE_{0}E_{1}$ et $OI_{0}I_{1}$ . Le triangle $OEE_{0}$ est donc rectangle et d'après les relations trigonométriques, $\displaystyle EE_{0}= tan \left( \frac{\pi}{6} \right)$ . D'où :

$\displaystyle P_{ext}=12\,tan \left( \frac{\pi}{6} \right)$

En déduire un encadrement de $\pi$ .

$\displaystyle P_{int} < 2\pi < P_{ext} \iff 3 < \pi < 6\,tan\left(\frac{\pi}{6}\right)$

… et enfin un polygone quelconque !

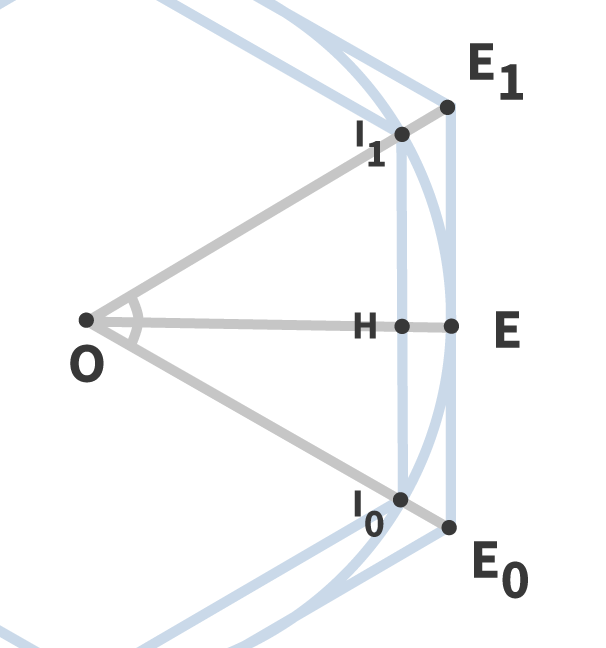
Un polygone est inscrit dans un cercle, lui-même inscrit dans un autre polygone.

On considère maintenant un polygone régulier de $n$ côtés.

Que vaut l'angle au centre d'un tel polygone ? En déduire la longueur d'un côté du polygone intérieur, puis son périmètre.

Dans un polygone régulier de $n$ côtés, l'angle au centre est égal à $\displaystyle \frac{2\pi}{n}$ . Le triangle formé par deux points successifs du polygone et le centre de celui-ci est un triangle isocèle. Ce triangle isocèle peut être divisé en deux triangles rectangles dans lesquels on applique les relations trigonométriques :

En suivant les notations de la figure ci-dessus, on obtient $\displaystyle sin \left( \frac{\pi}{n} \right) = HI_{1}$ , d'où :

$\displaystyle P_{int} = 2n\,sin\left(\frac{\pi}{n}\right)$

Comme précédemment, on remarque que le triangle formé par le centre du polygone et deux points du polygone extérieur (tel que l'un d'eux est situé sur le cercle) est un triangle rectangle. En déduire la longueur d'un côté du polygone extérieur, puis son périmètre.

En utilisant les notations de la figure ci-dessus, on obtient $\displaystyle tan \left( \frac{\pi}{n} \right) = EE_{0}$ , d'où :

$\displaystyle P_{ext} = 2n\,tan\left(\frac{\pi}{n}\right)$

En déduire un encadrement de $\pi$ pour un polygone à $n$ côtés.

$\displaystyle P_{int} < 2\pi < P_{ext} \iff n\,sin\left(\frac{\pi}{n}\right) < \pi < n\,tan\left(\frac{\pi}{n}\right)$

Tracer les deux courbes $\displaystyle f\left(x\right) = x\,sin \left( \frac{\pi}{x} \right)$ et $\displaystyle g\left(x\right) = x\,tan \left( \frac{\pi}{x} \right)$ dans une même fenêtre, pour des valeurs de $x$ allant de 3 à 20. Que constate-t-on ? Comment obtenir une approximation plus précise de $\pi$ ?

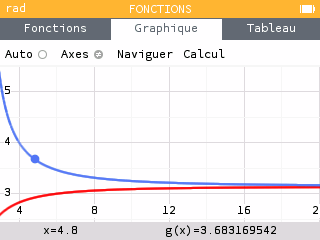
Les deux courbes tendent vers une même valeur à l'infini.

L'écart entre les deux courbes semble se réduire lorsque $x$ tend vers des valeurs très grandes. On peut poser l'hypothèse qu'elles admettent toutes les deux une asymptote horizontale en $x=\pi$ .

Pour réduire l'écart entre les valeurs de l'encadrement et se rapprocher de la valeur exacte de $\pi$ , il faudrait que $n$ soit très grand.

Avec un peu de python !

On aimerait réaliser un algorithme qui calcule l'écart entre les deux bornes de l'encadrement, et renvoie le nombre de côtés du polygone pour lequel cet écart dépasse une valeur $p$ .

Combien de côtés comporte le polygone pour lequel la différence entre le périmètre extérieur et le périmètre intérieur est inférieure à 0,01 ?

On peut aussi bien sûr utiliser l'application Suites pour déterminer ce seuil.