Fonction Smile
Valeur absolue Second degré Ensemble de définition Parité
Objectif
L'objectif de cette activité est d'amener les élèves à manipuler les fonctions de référence et leurs propriétés, en privilégiant l'expérimentation, afin de tracer un dessin de leur choix. Elle amène à la présentation de notions qui ne sont plus au programme mais peuvent constituer un prolongement intéressant du cours d'analyse.
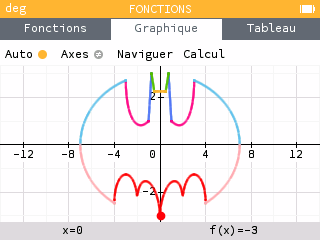
En 2011, un phénomène s'est répandu sur Internet auprès de tous les amoureux des mathématiques : un professeur était parvenu à reproduire la chauve-souris de Batman à l'aide d'une unique équation mathématique. On peut simplifier cette équation en 6 équations plus courtes et le principe paraît alors simple : chacune d'entre elles permet de représenter un morceau du dessin.
Nous allons essayer nous aussi de dessiner à l'aide des fonctions.
Fonction définie par morceaux
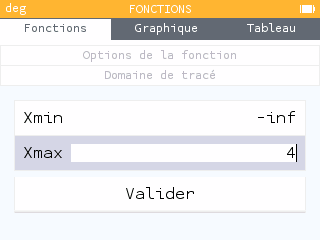
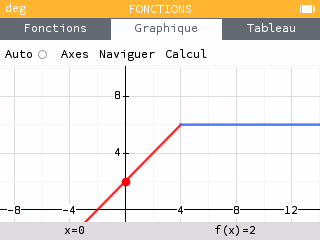
Une fonction définie par morceaux est une fonction dont l'expression diffère selon les intervalles de son domaine de définition. On propose par exemple la fonction suivante :
Sur la calculatrice, on entre deux fonctions distinctes, cependant on utilise le menu de chacune de ces fonctions pour modifier leur domaine de définition.
Fonction valeur absolue
On connaît la notation de la valeur absolue. On l'utilise, par exemple, pour exprimer la distance entre deux points. Sa valeur est toujours positive. Ainsi, la fonction valeur absolue est une fonction définie par morceaux :
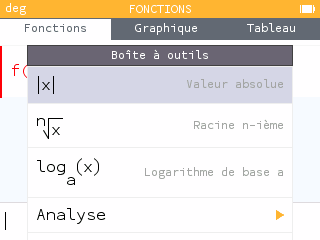
Sur la calculatrice, on peut directement trouver cette fonction en passant par la boîte à outils. Son dessin est assez inhabituel puisque très "pointu" !
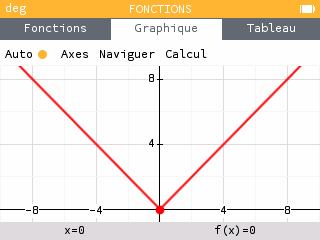
-
Quelle est la parité de la fonction valeur absolue ?
La fonction semble paire. Démontrons-le par le calcul :
-
On aimerait modifier la fonction afin que sa représentation graphique soit inversée par rapport à l'axe des abscisses et que la "pointe" soit dirigée vers le haut. Quelle est la définition de cette nouvelle fonction ?
-
On aimerait maintenant modifier la fonction initiale afin que sa représentation graphique soit décalée vers le haut. Proposer une fonction qui remplisse cette condition.
-
Même question pour que la représentation graphique de la fonction soit décalée vers la droite.
La fonction aura une forme . Si , la courbe sera décalée vers la droite. Si , elle sera décalée vers la gauche.
-
Même question pour que la représentation graphique de la fonction soit plus ou moins évasée.
La fonction aura une forme . Si , la courbe représentative de la fonction sera plus large. A l'inverse, si , la courbe sera plus étroite.
La fonction smile
On propose d'écrire une fonction mathématique définie en trois morceaux dont la représentation graphique sera un visage stylisé.
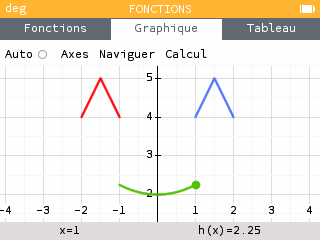
-
Au vu de leur représentation graphique, de quels types seront les fonctions associées aux yeux ? Et au sourire ?
On utilisera une fonction composée de la valeur absolue pour tracer les yeux, une fonction du second degré pour le sourire.
-
Rechercher des exemples de fonctions dont le résultat s'approche des éléments du dessin proposé.
On attend des fonctions de type et pour les fonctions des yeux.
-
Proposer une fonction définie par morceaux qui respecte la symétrie demandée.
On propose par exemple la fonction suivante :
-
Pour les élèves les plus intrépides : on cherche à reproduire très exactement le dessin précédent. L'oeil droit admet un sommet en et passe par les points de coordonnées et . Établir le système d'équations correspondant à l'énoncé et le résoudre.
D'après les indications proposées, la fonction correspondant à l'oeil droit doit être de la forme avec d'où :
Pour résoudre le système en tenant compte de la valeur absolue, il faudra résoudre quatre systèmes d'équations. L'un d'eux admet et est donc à écarter. Deux autres admettent . Il reste donc la solution telle que :
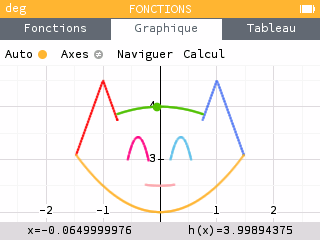
A vos plus beaux dessins !
Valeurs "interdites" et ensemble de définition
Comme nous l'avons expliqué en introduction, la fonction de Batman est une fonction unique, et surtout, une fonction qui n'est pas définie par morceaux. Son expression est telle qu'elle n'admet de représentation graphique que sur des intervalles restreints. Nous allons nous intéresser à l'un des extraits de cette équation :
Quelle est la représentation graphique de cette fonction ? Quel est son ensemble de définition ?
Commenter l'utilisation d'une telle expression.
La fonction est représentée par une droite horizontale d'équation . Cependant, la fonction étant définie sur un intervalle restreint, sa représentation graphique ne s'étend qu'entre et .
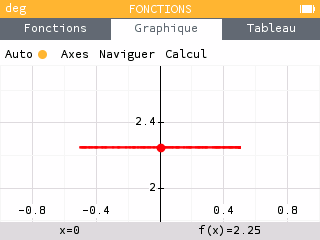
En effet, l'utilisation de la racine carrée réduit l'ensemble de définition. Le radicande doit être positif ou égal à 0, ce qui implique que le numérateur et le dénominateur de la fonction sont de même signe. Le numérateur étant toujours positif, l'ensemble de définition est restreint aux valeurs de pour lesquelles le dénominateur l'est aussi (strictement positif, car une dénominateur ne peut pas être égal à 0), autrement dit pour lesquelles :
On remarque que la fraction exprimée sous le radical est égale à 1. Sa seule utilité était donc bien de représenter une portion de la droite d'équation en utilisant les propriétés de la racine carrée et de la valeur absolue.
C'est ce même principe qui est utilisé pour chacune des équations de la fonction de Batman !
Pour en savoir plus sur l'équation de Batman et les transformations mathématiques permettant de modifier une représentation graphique : The Batman Equation - partie 1 et partie 2 (en anglais).