Indice de Gini

L'indice de Gini, ou coefficient de Gini, est un indicateur statistique permettant d'étudier la répartition d'une variable au sein de la population. On l'utilise fréquemment pour mesurer les inégalités. Par exemple, son calcul permet d'étudier la répartition des salaires, du patrimoine ou de l'impôt sur le revenu dans une population.

Cet outil a été développé par la statisticien Corrado Gini et prend la forme d'un nombre compris entre 0 et 1.

Courbe de Lorenz

L'indice de Gini se calcule à partir d'une courbe de Lorenz. La courbe de Lorenz, du nom de son inventeur, est une représentation graphique permettant de visualiser la distribution d'une variable au sein d'une population.

Pour qu'une fonction puisse modéliser une telle répartition, elle doit obéir à plusieurs critères :

• La fonction doit être continue, croissante et convexe sur $\left[0 ; 1\right]$ ;

• $f(0)=0$ et $f(1)=1$ ;

• $f(x) \leqslant x$ sur $\left[0 ; 1\right]$.

On s'intéresse à la fonction $f$ définie telle que :

$f(x)=\begin{cases} 0 & \text{si } x \in \left[0;0.5\right[ \\ \displaystyle\frac{3}{2}x^2-\frac{1}{4}x-\frac{1}{4} & \text{si } x \in \left[0.5 ; 1\right] \end{cases}$

On souhaite, dans un premier temps, montrer que la courbe représentative de la fonction $f$ est bien une fonction de Lorenz.

1. On admet que la fonction est continue sur l'intervalle $\left[0;1\right]$.

   Montrer qu'elle est croissante et convexe sur ce même intervalle.

La fonction est constante sur $\left[0;0.5\right[$. Sa dérivée est donc nulle, de même que sa dérivée seconde.

Sur l'intervalle $\left[0.5 ; 1\right]$, on a $\displaystyle f'(x)=3x-\frac{1}{4}$ et $f''(x)=3$. La dérivée et la dérivée seconde sont positives sur $\left[0.5 ; 1\right]$.

D'où $f'(x) \geqslant 0$ sur $\left[0 ; 1\right]$ : la fonction est bien croissante sur cet intervalle.

Et $f''(x) \geqslant 0$ sur $\left[0 ; 1\right]$ : la fonction est bien convexe sur cet intervalle.

2. Montrer que $f(0)=0$ et $f(1)=1$, puis dessiner le tableau de variation sur la fonction sur $\left[0 ; 1\right]$.

$\begin{array}{|c|lcr|} \hline x & 0 & & 1 \\ \hline & & & 1 \\ f\left(x\right) & & \nearrow & \\ & 0 & & \\ \hline \end{array}$

3. On propose d'étudier sur l'intervalle $\left[0 ; 1\right]$, le signe de la différence $x-f(x)$.

   En déduire la position relative de la courbe représentative de la fonction $f(x)$ et de la droite d'équation $y=x$.

Sur l'intervalle $\left[0 ; 0,5\right[$, on a $x-f(x)=x$. La différence est positive sur cet intervalle.

Sur l'intervalle $\left[0,5 ; 1\right]$, on a $\displaystyle x-f(x)=x - (\frac{3}{2}x^2 - \frac{1}{4}x -\frac{1}{4}) = -\frac{3}{2}x^2 + \frac{5}{4}x + \frac{1}{4}$.

Il s'agit d'une fonction du second degré, de signe positif entre ses racines. Ces racines nous sont données par la calculatrice.





La différence $x-f(x)$ est toujours positive sur l'intervalle $\left[0 ; 1\right]$, cela signifie que la courbe représentative de la fonction $f$ est toujours située en-dessous de la droite d'équation $y=x$.

Une fois ces éléments démontrés, notre fonction peut être utilisée pour modéliser la répartition d'une variable.

Afin de comprendre le calcul du coefficient de Gini, nous allons maintenant pouvoir tracer sur la calculatrice la courbe représentative de la fonction $f$, ainsi que la droite d'équation $y=x$.

Indice de Gini

On s'intéresse à la répartition du patrimoine au sein d'une population, modélisée par la fonction $f$ définie telle que :

$f(x)=\begin{cases} 0 & \text{si } x \in \left[0;0.5\right[ \\ \displaystyle\frac{3}{2}x^2-\frac{1}{4}x-\frac{1}{4} & \text{si } x \in \left[0.5 ; 1\right] \end{cases}$

1. Le point de coordonnées $(0,75 ; 0,25)$ se trouve sur la courbe : cela signifie que les 75% de la population les plus modestes se partagent 25% du patrimoine.

   Déterminer le pourcentage de la population qui se partage les premiers 80% du patrimoine ?

En cherchant l'antécédent de 0,8 avec la calculatrice, on obtient 0,924 : cela signifie que les 92,4% de la population les plus modestes se partage 80% du patrimoine. Ou, à l'inverse, que les 7,6% les plus aisés se partagent 20% du patrimoine.

2. On a représenté sur notre graphique la droite d'équation $y=x$. Pourquoi cette droite représente-t-elle la répartition la plus égalitaire possible ?

Si l'on considère cette droite comme une courbe de Lorenz, alors $x$% de la population se répartit $x$% de la variable (ici, le patrimoine). Il s'agit donc bien d'une répartition égalitaire.

3. L'indice de Gini correspond au rapport de l'aire située entre la courbe de Lorenz et la droite (en rouge sur le graphique), que l'on appelle aire de concentration, par rapport à l'aire située entre la droite et l'axe des abscisses (soit la somme des surfaces bleue et rouge ci-dessous, l'équivalent d'un triangle de 0.5 unité d'aire).

   

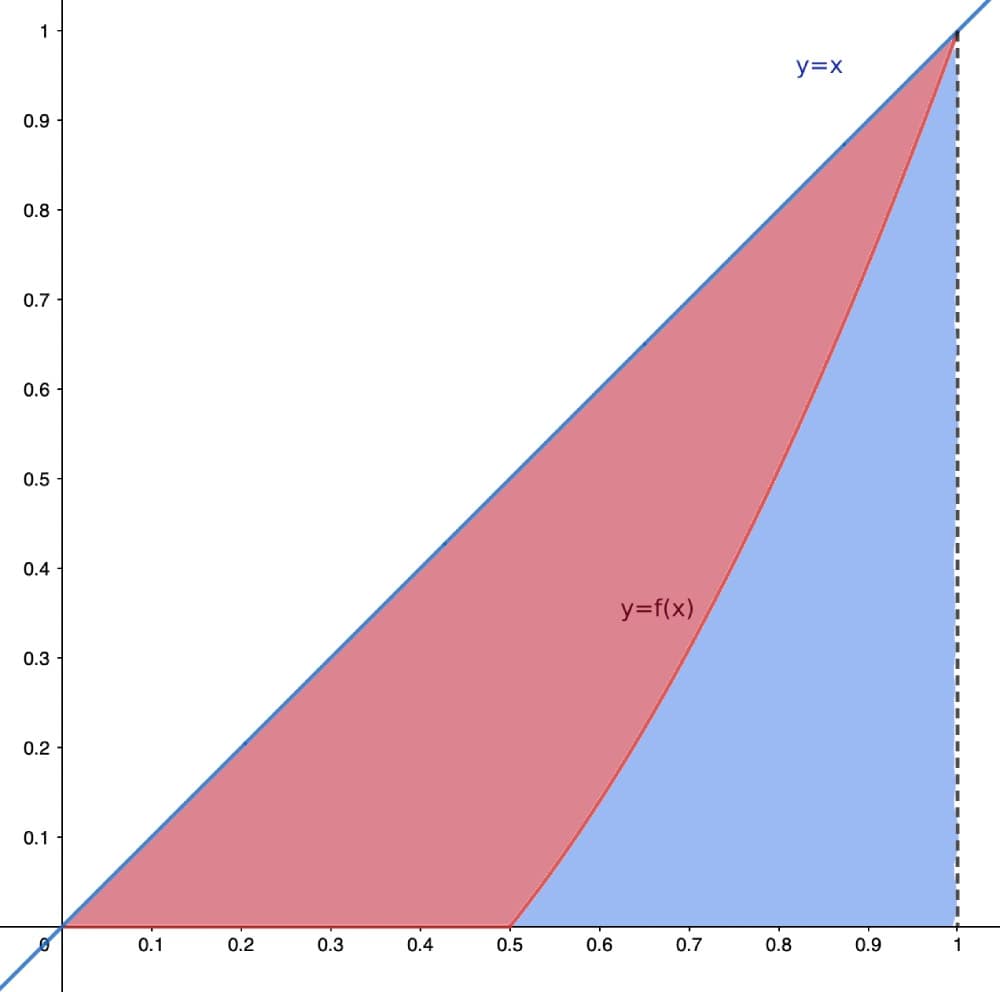
   On a indiqué précédemment que cet indice prenait une valeur comprise entre 0 et 1. Quelle interprétation pourrait-on faire d'un indice de Gini égal à 0 ou à 1 ?

Si l'indice de Gini est égal à 0, cela signifie que l'aire comprise entre la courbe de Lorenz et la droite d'équation $y=x$ est à égale à 0. Les deux courbes sont donc confondues et la répartition est parfaitement égalitaire.

A l'inverse, si l'indice de Gini est égal à 1, cela signifie que l'aire comprise entre la courbe de Lorenz et la droite d'équation $y=x$ est identique à celle du triangle. La courbe est donc confondue avec l'axe des abscisses : la répartition est parfaitement inégalitaire.

4. Calculer $\int_{0.5}^1 f(x) \mathrm{d}x$. En déduire la valeur du coefficient de Gini.

Une primitive de la fonction $f(x)$ sur $\left[0.5 ; 1\right]$est $F(x)=\displaystyle \frac{x^3}{2}-\frac{x^2}{8}-\frac{x}{4}$ D'où :

$\displaystyle \int_{0.5}^1 f(x) \mathrm{d}x = F(1) - F(0.5) = \frac{1}{8}-(\frac{1}{16} - \frac{1}{32} - \frac{1}{8}) = \frac{7}{32}$

D'où une aire de concentration (aire rouge) égale à $0,5 - \frac{7}{32} = \frac{9}{32}$.

On en déduit que l'indice de Gini est égal à $\frac{9}{16}$ soit environ 0,5625.

5. La population voisine possède un indice de Gini égal à 0,42 pour la même variable. La répartition est-elle plus égalitaire ?

On a vu que plus l'indice de Gini était proche de 0 et plus la répartition était égalitaire. Cette population voisine a un indice de Gini plus faible, donc une répartition du patrimoine plus égalitaire.