Calcul d'une intégrale par la méthode des rectangles
Etude de fonction Calcul intégral Programmation Python
Objectif
Réalisation d'un programme Python pour obtenir par approximation l'aire se trouvant sous une gaussienne. L'activité permet une première approche de la loi normale.
On s'intéresse à l'aire comprise sous la représentation graphique d'une fonction définie sur par :
Cette fonction étant très complexe à primitiver, nous allons programmer une fonction en Python qui nous permettra d'aboutir à une bonne approximation de la valeur recherchée.
Etude de la fonction
-
Calculer les limites de la fonction aux bornes de l'ensemble de définition.
-
Dresser le tableau de variation de la fonction.
-
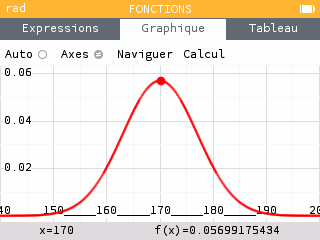
Représenter graphiquement la courbe sur l'intervalle .
On calcule .
La fonction est croissante lorsque et décroissante pour .

Approximation par la méthode des rectangles
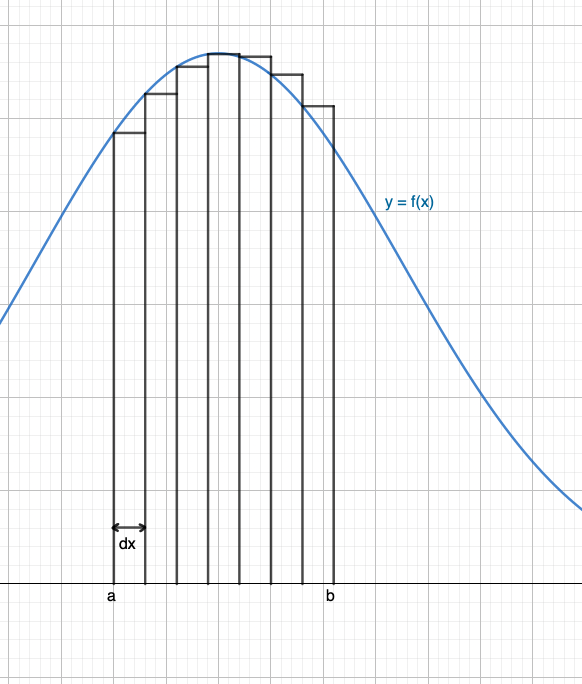
On procède à un découpage de la courbe par rectangles de largeur identique , tout comme sur le dessin ci-contre.
L'objectif est d'obtenir une approximation de la surface comprise sous la courbe entre et en faisant la somme des aires des rectangles.
-
Que faut-il faire pour que l'approximation obtenue soit la plus proche possible du résultat recherché ?
-
On considère l'aire comprise sous la courbe entre deux abscisses et . Exprimer la largeur en fonction de , et le nombre de rectangles découpant cet espace.
-
Exprimer en fonction de la hauteur du premier rectangle au point d'abscisse . Quelle est la hauteur du second rectangle situé au point d'abscisse ?
-
On propose d'écrire une fonction
approx_rect(n,x_inf,x_sup)permettant de calculer l'intégrale d'une fonction (que l'on aura préalablement définie dans une autre fonction) entre deux bornesx_infetx_suppar un découpage en rectangles.On utilisera dans ce programme deux variables
x, qui évolue entre les deux bornes, etsomme, qui stocke la somme des rectangles au cours du calcul. Comment sont initialisées ces deux variables au début du programme ? -
Compléter l'algorithme suivant afin d'obtenir le résultat souhaité :
from math import * def f(x): return (1/(7*sqrt(2*pi)))*exp(-((x-170)**2)/98) def approx_rect(n,x_inf,x_sup): somme= ... x= ... dx= ... while(x< ... ): somme=somme+dx*f(x) x+=dx return ...
Pour que le résultat soit le plus précis possible, il faut augmenter le nombre de rectangles et donc diminuer la largeur de chacun d'entre eux.
Le premier rectangle à partir du point d'abscisse admet pour hauteur . Le second rectangle à partir du point d'abscisse admet pour hauteur .
Au début du programme, x=x_inf et somme=0.
Un script est disponible sur cette page.
Exécution de l'algorithme et loi normale
-
Quelle valeur obtient-on lorsque l'on exécute le programme pour les valeurs , et ?
-
Dans notre cas, la fonction de densité permet d'étudier la répartition des tailles des adultes dans la population française, de moyenne (cm) et d'écart-type (cm).
Comment interpréter le nombre obtenu lorsqu'on a exécuté le programme entre 120 et 230 ?
-
Exécuter le programme pour , et . Comment interpréter ce résultat ?
-
Même question pour une exécution entre et .
-
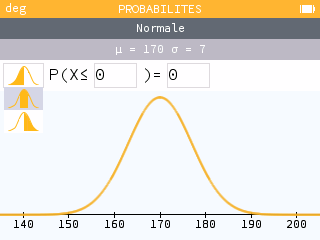
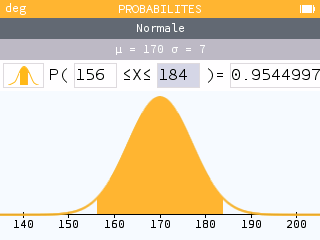
Rendez-vous maintenant dans l'application Probabilités de la calculatrice : sélectionner Normale dans le menu puis entrer les paramètres et définis plus haut. Modifier l'icône en haut à gauche de façon à sélectionner le second dessin, puis encadrer X entre 156 et 184. Et maintenant… admirez !
Le programme retourne 1.
La fonction est ce que l'on appelle une fonction de densité, c'est-à-dire qu'il s'agit d'une fonction continue et positive sur un intervalle telle que son intégrale sur cet intervalle est égale à 1. Dans ce cas particulier, la courbe en cloche que l'on obtient lorsque l'on représente graphiquement cette fonction est appelée courbe de Gauss.
Les courbes de Gauss sont utilisées car elle traduisent une réalité statistique souvent observée sur des grandes populations pour des phénomènes aléatoires : les effectifs se répartissent autour d'une valeur centrale en suivant une courbe en cloche dont on peut connaître l'équation. C'est vrai lorsque l'on s'intéresse à la masse exacte d'un grand nombre de boîtes d'une même conserve, ou à la taille des chats adultes en région parisienne. On dit que leur répartition suit une loi normale.
Cela signifie que l'aire se trouvant sous la courbe est égale à 1. Etant donné qu'il s'agit d'une fonction de densité permettant d'étudier la répartition des tailles dans la population française, on peut supposer que les personnes mesurant entre 120 et 230 cm représentent (approximativement) 100% de la population.
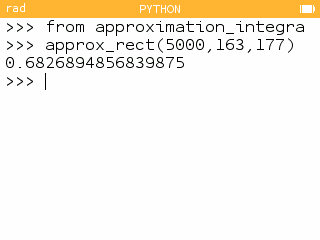
L'aire se trouvant sous la courbe entre 163 et 177 est égale à environ 0,68. On en déduit qu'approximativement 68% des français mesurent entre 163 et 177 cm.
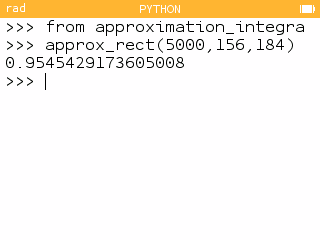
L'aire se trouvant sous la courbe entre 156 et 184 est égale à environ 0,95. On en déduit qu'approximativement 95% des français mesurent entre 156 et 184 cm.
Un peu plus de Python pour les plus rapides !
Ecrire une fonction approx_trapeze(n,x_inf,x_sup) permettant une autre approximation de la surface située sous la courbe par un découpage en trapèzes.
Un script est disponible sur cette page.