L'équation de Tsiolkovski

Contexte

L'un des "pères" de l'aéronautique était un professeur de mathématiques du nom de Constantin Tsiolkovski. Né en Russie pendant la seconde moitié du XIXe siècle, ce grand amateur de Jules Verne est l'un des premiers à théoriser le vol spatial. En 1903, il démontre par le calcul qu'il est possible d'envoyer des fusées dans l'espace, équipées de moteurs à réaction. Si ses recherches sont d'abord passées inaperçues, elles ont néanmoins posé les bases théoriques de toute notre industrie spatiale, en proposant l'utilisation d'ergols liquides et de fusées à étages. L'un des cratères de la "face cachée" de la Lune porte aujourd'hui son nom.

Accélération, vitesse et intégrale

L'équation de Tsiolkolvski a pour objectif de calculer la capacité d'incrément de vitesse $\Delta v$ d'un satellite, c'est-à-dire la différence de vitesse que connaît celui-ci avant et après une propulsion (en valeur absolue).

Pour simplifier les calculs et nous affranchir de la gravité, nous allons considérer un véhicule se situant déjà dans l'espace et souhaitant réaliser une poussée afin de modifier sa vitesse.

1. Relier accélération et vitesse en termes de dérivée.

   On sait que l'accélération est une variation de la vitesse au cours du temps. Autrement dit, l'accélération est une fonction dérivée de la vitesse en fonction du temps : $\displaystyle a \left( t \right) = \frac{\mathrm{d}}{\mathrm{d} t} v \left( t \right)$

2. Vitesse et accélération sont des fonctions continues, on utilisera donc une intégration pour réaliser l'opération inverse de la dérivation. Proposer une formule permettant de calculer $\Delta v$, variation de vitesse entre les moments $t_{1}$ et $t_{2}$, à l'aide d'une intégrale.

   $\Delta v = v\left(t_{2}\right)-v\left(t_{1}\right)=\int_{t_{1}}^{t_{2}}a(t)\mathrm{d}t$

   L'utilisation d'une intégrale dans ce calcul permet de prendre précisément en compte toutes les variations de $v$ au cours du temps.

Conservation de la quantité de mouvement

Lors d'une impulsion, l'engin spatial va éjecter des gaz issus de la combustion des carburants (ergols) à vitesse constante $\vec{v}_{e}$ dans la direction opposée à la trajectoire suivie par l'engin. On rappelle que la quantité de mouvement d'un système est égale au produit de la masse du système par son vecteur vitesse. Ainsi, pour un vaisseau de masse initiale $m$ et de vecteur vitesse $\vec{v}$, la quantité de mouvement initiale est égale à $\vec{p}=m\times\vec{v}$ .

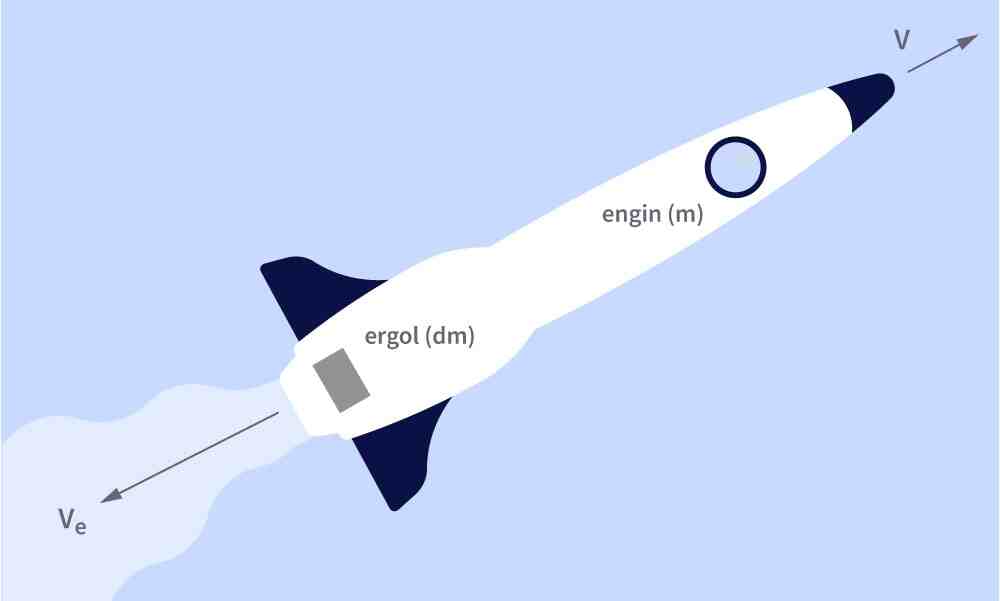
1. Exprimer, dans un premier temps, la quantité de mouvement de l'engin spatial au cours de la poussée. On notera $\mathrm{d} m$ la variation de la masse de carburant après un instant $\mathrm{d}t$, avec $\mathrm{d} m \lt 0$, et $\mathrm{d} \vec{v}$ la vitesse gagnée par la fusée pendant cet instant.

   Exprimer, dans un second temps, la quantité de mouvement relative à la masse d'ergols éjectés.

   Concernant la quantité de mouvement de l'engin :

   $\left(m+\mathrm{d} m\right)\times\left(\vec{v}+\mathrm{d}\vec{v}\right)$

   Concernant celle des ergols expulsés :

   $\left(-\mathrm{d} m\right)\times\left(\vec{v}_{e}+\vec{v}+\mathrm{d}\vec{v}\right)$

2. La quantité de mouvement de l'ensemble du système est conservée, c'est-à-dire qu'elle est identique à la quantité de mouvement initiale du vaisseau. Autrement dit :

   $m \left( t \right) \vec{v} \left( t \right) = m \left( t + \mathrm{d}t \right) \vec{v} \left( t + \mathrm{d}t \right)$

   Écrire puis réduire l'équation afin d'isoler $\mathrm{d} \vec{v}$.

   $m\vec{v}=\left(m+\mathrm{d} m\right)\left(\vec{v}+\mathrm{d}\vec{v}\right) +\left(-\mathrm{d} m\right)\left(\vec{v}_{e}+\vec{v}+\mathrm{d}\vec{v}\right)$

   $\vec{0}=m\,\mathrm{d}\vec{v}+\left(-\mathrm{d} m\right)\,\vec{v}_{e}$

   $m\,\mathrm{d}\vec{v}=\mathrm{d} m\,\vec{v}_{e}$

   $\displaystyle \mathrm{d}\,\vec{v}=\frac{\mathrm{d} m}{m} \vec{v}_{e}$

3. A l'aide de l'intégration, proposer une expression de $\Delta \vec{v}$, variation de vitesse entre les instants $t_{1}$ et $t_{2}$, telle que :

   $\displaystyle \Delta \vec{v} = \int_{v_{1}}^{v_{2}} \mathrm{d}\vec{v} = \int_{t_{1}}^{t_{2}} \frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\,\mathrm{d}t$

   $\displaystyle \Delta \vec{v} = \int_{t_{1}}^{t_{2}} \frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\,\mathrm{d}t= \vec{v}_{e}\int_{t_{1}}^{t_{2}}\frac{1}{m}\frac{\mathrm{d}m}{\mathrm{d}t} \mathrm{d}t$

   $\displaystyle \Delta \vec{v} = \vec{v_{e}}\int_{m \left( t_{1} \right) }^{m \left( t_{2} \right) }\frac{1}{m}\,\mathrm{d}m = \vec{v_{e}}\int_{m_{1}}^{m_{2}}\frac{1}{m}\,\mathrm{d}m = -\vec{v_{e}}\,\ln(\frac{m_{1}}{m_{2}})$

4. Les vecteurs $\vec{v}$ et $\vec{v}_{e}$ étant de sens contraires, on obtient en termes de normes :

   $\displaystyle \Delta v = v_{e}\,\ln(\frac{m_{1}}{m_{2}})$

   On s'intéresse maintenant à la masse $m_{man}$ nécessaire à la réalisation de la manœuvre. Autrement dit, on pose $m_{man}=m_{1}-m_{2}$. Proposez une expression de $m_{man}$.

   $\displaystyle\frac{m_{1}}{m_{2}}=\mathrm{e}^{\frac{\Delta v}{v_{e}}}$

   $\displaystyle m_{man}=m_{1}-m_{2}=m_{2}\,\left(\mathrm{e}^{\frac{\Delta v}{v_{e}}}-1\right)$

Applications

1. On considère un engin spatial doté d'ergols dont la vitesse d'éjection est de 4,4 km/s. Quelle poussée peut espérer gagner cet engin pesant initialement 150 tonnes en brûlant 100 tonnes de ses ergols ?

   

   Le résultat est donné en m/s d'où :

   $\displaystyle\Delta v = 4,8 \,\mathrm{km/s}$

2. On considère l'engin précédent. Tracer la courbe représentative de la fonction exprimant le $\Delta v$ en fonction de la masse $m_{2}$ restante dans l'engin et proposer une interprétation de cette courbe. Comparer avec un engin dont la vitesse d'éjection des ergols est de 6 km/s.

   

   

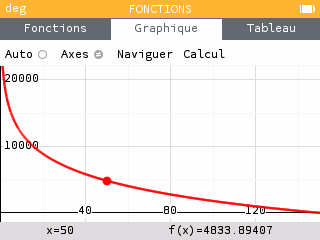
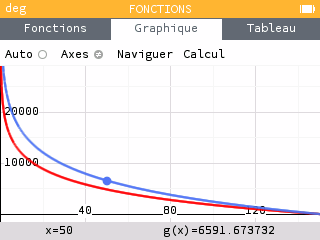
   La masse restante dans l'engin ne pouvant être ni négative, ni supérieure à 150, on propose d'utiliser une fenêtre allant de 0 à 150 pour les valeurs de $x$.

   La courbe est décroissante : plus il reste des ergols dans l'engin, moins le $\Delta v$ est important. En effet, la combustion des ergols est nécessaire pour modifier le vecteur vitesse. La fonction n'est pas définie en zéro : il est de toutes façons impossible d'avoir une masse nulle à l'issue de la combustion. La masse de l'engin, même vidé de son carburant, reste importante, ce qui explique pourquoi la variation de vitesse ne peut pas dépasser un certain seuil.

   Lorsque la vitesse d'éjection des ergols est plus importante, la poussée l'est aussi.

3. A l'inverse, un engin spatial de 30 tonnes (à vide) se déplaçant à une vitesse de 8 km/s nécessite une poussée lui permettant d'atteindre 14 km/s. On utilise des ergols dont la vitesse d'éjection est de 4,4 km/s. Quelle masse est nécessaire à cette propulsion ?

   

   $\displaystyle m_{man}=87\,\mathrm{t}$

4. Comme précédemment, on propose de tracer la courbe représentative de $m_{man}$ en fonction de la poussée $\Delta v$. Proposer une interprétation de cette courbe.

   

   

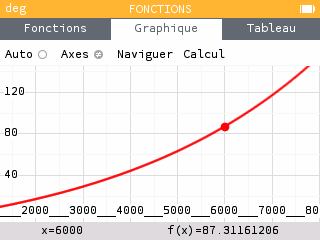
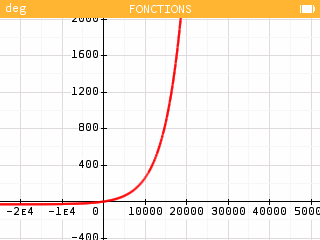
   La courbe est croissante : plus la poussée est importante, plus la masse nécessaire à la manoeuvre l'est aussi. On remarque que cette fonction croit exponentiellement, ce qui signifie qu'une poussée plus importante nécessite une augmentation drastique du carburant embarqué.... d'où la nécessité d'utiliser plusieurs étages !