Hexagrammes et trigrammes

1. Prenons pour commencer trois lignes que l'on appelle trigramme. Chacune de ces lignes peut être soit continue, soit brisée. On peut modéliser ces lignes à l'aide de bâtonnets : trois bâtonnets pour une ligne pleine, deux bâtonnets séparés d'un espace pour une ligne brisée.

   Combien de trigrammes différents peut-on constituer ?

   Chaque ligne possède deux états, et la figure est composée de 3 lignes. Il existe donc $2^{3}$ soit 8 possibilités.

2. Un hexagramme est composé de deux trigrammes, soit 6 lignes au total. Combien de dessins différents peut-on obtenir ?

   Chaque ligne possède deux états, et la figure est composée de 6 lignes. Il existe donc $2^{6}$ soit 64 possibilités.

   On pourra faire remarquer que c'est le principe multiplicatif qui permet de retrouver les 64 hexagrammes à partir du résultat précédent. Soit A l'ensemble des trigrammes supérieurs et B l'ensemble des trigrammes inférieurs. Le produit cartésien de A et B constitue l'ensemble des hexagrammes existant, formés d'un élément de A et d'un élément de B.

3. Si l'on sait que la première ligne de la figure est continue, combien dénombre t-on d'hexagrammes possibles ?

   La première ligne est continue mais les cinq autres ont deux états possibles. Il existe donc $2^{5}$ soit 32 figures possibles.

4. On sait qu'une figure est composée de 5 lignes brisées. Combien d'hexagrammes correspondent à cette description ?

   On utilise les combinaisons : Boîte à outils > Probabilités > Dénombrement. Il n'y a qu'une seule ligne pleine sur 6, qui peut occuper n'importe laquelle des 6 positions.

   Chercher les positions des 5 lignes brisées revient à chercher les positions de la ligne pleine.

   

   

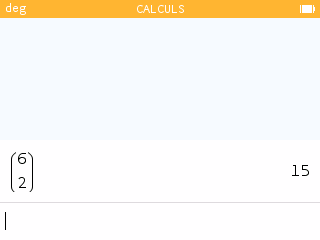
5. On sait qu'une figure est composée de deux lignes brisées, les quatre autres sont continues. Combien d'hexagrammes correspondent à cette description ?

   

Générer aléatoirement un hexagramme

Ecrire un programme à l'aide de Kandinsky afin de générer aléatoirement un hexagramme.

Le module Kandinsky permet de colorer des pixels ou des rectangles à l'aide d'instructions basiques. On importe tout d'abord la totalité des fonctions du module Kandinsky à l'aire d'une ligne from kandinsky import *.

On peut ensuite utiliser la fonction fill_rect(x,y,l,h,couleur afin de colorer un rectangle de largeur l et de hauteur h au point de coordonnées (x ; y). Le rectangle sera tracé à partir de ces coordonnées vers la droite et le bas de l'écran. Le point tout en haut à gauche de l'écran correspond aux coordonnées (0 ; 0) et celui en bas à droite correspond aux coordonnées (320 ; 222).

Les couleurs doivent être définies au préalable en utilisant le système RGB à l'aide la commande nom = color(nb, nb, nb), chaque nombre ayant une valeur comprise entre 0 et 255.

Des séries d'hexagrammes

1. On décide de générer successivement 2 hexagrammes. Quelle est la probabilité pour qu'ils soient identiques ?

   On rappelle qu'il existe 64 hexagrammes possibles. La probabilité est donc de $\displaystyle\frac{1}{64}$.

2. On décide maintenant de générer successivement 3 hexagrammes. Quelle est la probabilité pour que ces trois hexagrammes soient identiques ?

   Les deux hexagrammes doivent correspondre au premier, qui représente une possibilité parmi 64. La probabilité est donc de $\displaystyle\frac{1}{4096}$.

3. Quelle est la probabilité sur ces trois hexagrammes générés successivement que deux d'entre eux soient identiques ?

   La probabilité d'avoir deux hexagrammes identiques est de 1/64. Cependant, il existe plusieurs configurations pour obtenir deux hexagrammes identiques, il existe $\displaystyle\binom{3}{2}$ soit 3 combinaisons possibles.

   La probabilité d'obtenir deux hexagrammes identiques est donc de $\displaystyle\frac{3}{64}$.

4. Quelle est la probabilité sur 5 hexagrammes d'en obtenir deux identiques ?

   $p = \binom{5}{2} \times \frac{1}{64} = \frac{5}{32}$.

5. Imaginons que l'on modifie le programme de manière à ne pas pouvoir générer deux hexagrammes identiques. Combien de séries différentes existe-t-il si l'on génère successivement 3 hexagrammes ?

   Il existe 64 possibilités pour le premier, 63 pour le deuxième, et ainsi de suite. Attention, ici l'ordre compte puisque l'on s'intéresse à la série de figures. Il s'agit donc d'un arrangement de 3 éléments parmi 64.

   Pour calculer des arrangements à l'aide de la calculatrice : Boîte à outils > Probabilités > Dénobrement."

---

Pour plus d'informations sur l'analyse de Leibniz à propos du Yi-King :

• Le texte original disponible sur ce site et sa transcription sur cet autre site.
• Une analyse en anglais par ici.